冀教版七年级上册数学 2.7角的和与差 课件(共24张)
文档属性
| 名称 | 冀教版七年级上册数学 2.7角的和与差 课件(共24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 249.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 18:24:03 | ||
图片预览







文档简介
(共24张PPT)
2.7 角的和与差
A
C
B
O
图中共有几个角?
它们之间有什么关系?
图中∠AOC是∠AOB
和∠BOC的和,记作
∠AOC=∠AOB+∠BOC
图中∠AOB是∠AOC和∠BOC的差,
记作∠AOB=∠AOC-∠BOC
那么,图中∠AOC-∠AOB=
∠BOC
认识角的和差
C
B
O
A
如图(1)若∠AOC=32 ° ,∠BOC=43° 则∠AOB= ____
若已知 ∠AOB = 68 ° ∠BOC=40°
则∠AOC=____
75 °
28 °
23°31′25″
42°37′56″
42°37′56″
23°31′25″
66°9′21″
19°6′31″
O
B
A
C
∠AOC =∠BOC=
∠AOB =2∠AOC =2∠BOC
角平分线
∠AOB
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线。
A
B
C
D
O
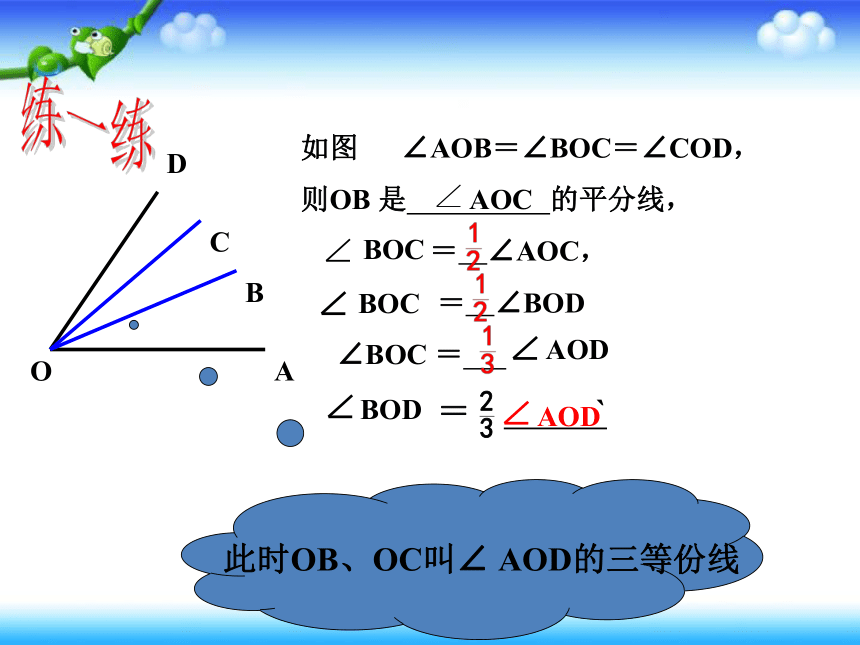
如图 ∠AOB=∠BOC=∠COD,
则OB 是 的平分线,
= ∠AOC,
= ∠BOD
∠BOC =
= `
AOC
BOC
BOC
AOD
BOD
AOD
此时OB、OC叫∠ AOD的三等份线
练一练
如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
D
C
B
A
O
∠AOC =∠____ + ∠ __
∠AOC= ∠____-∠ __
∠BOD - ∠COD= ∠ __
∠BOC= ∠AOC - ∠ __ = ∠BOD - ∠ __
∠AOB= ∠____ - ∠____ - ∠____
∠AOD = ∠____+ ∠ __+ ∠____
BOC
BOC
AOB
DOC
AOD
AOB
COD
AOD
BOC
COD
AOB
BOC
COD
填空
例
。
C
O
A
B
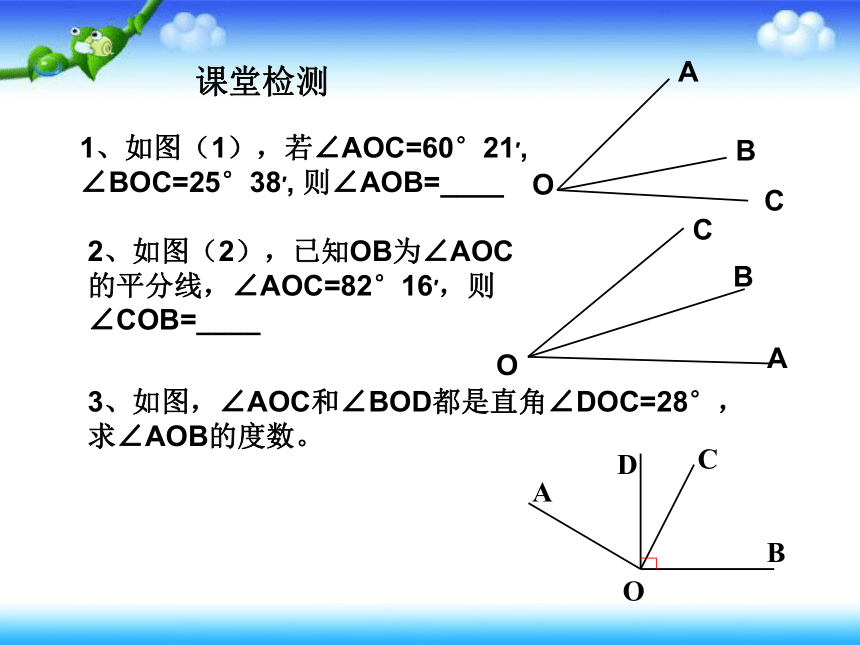
1、如图(1),若∠AOC=60°21′, ∠BOC=25°38′, 则∠AOB=____
A
O
B
C
2、如图(2),已知OB为∠AOC的平分线,∠AOC=82°16′,则∠COB=____
O
C
B
A
课堂检测
3、如图,∠AOC和∠BOD都是直角∠DOC=28°,求∠AOB的度数。
A
B
C
D
O
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB,求∠EOF的大小?
思考:
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
=1/2∠AOC+1/2∠COB
=1/2(∠AOC+∠COB)
=90°
∴∠EOC=1/2∠AOC,
∠COF=1/2∠COB
(角平分线的定义)
∵∠AOB=∠AOC+∠COB=180°
(平角的定义)
A
B
E
C
F
O
思考
如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,
求∠BOC的度数?
A
B
C
D
O
解:∵∠AOD=∠AOB+∠BOD=114°
∴∠AOB=1/3∠AOD=38°
∵OC平分∠AOD
∴∠AOC=1/2∠AOD=57°
(角平分线的定义)
∴∠BOC=∠AOC-∠AOB
∠BOD=2∠AOB
=57°-38°
=19°
解:
例
你能用三角板拼出一些特殊角吗?
利用三角尺还可以画出哪些度数的角?
30°、45°、60°、90°、15°、75°、105°、120°、135°、150°、 180°
(15的整数倍)
探究:
75°
15°
4
画出一个平角∠AOB,画一个直角∠CDE,并标出这两个角的度数,然后过这个角的顶点任意画一条射线OM和ON,并记为∠AOM=∠1,∠BOM=∠2,∠CDN=∠3,∠EDN=∠4。观察这两个角个图形有什么发现。
2
1
M
180°
90°
C
E
N
3
A
B
O
·
·
·
D
动动手,画一画。
90°
E
N
D
3
画出一个平角∠AOB,画一个直角∠CDE,并标出这两个角的度数,然后过这个角的顶点任意画一条射线OM和ON,并记为∠AOM=∠1,∠BOM=∠2,∠CEN=∠3,∠EDN=∠4。观察这两用角个图形有什么发现。
探 究
1
B
O
M
·
·
180°
A
O
M
2
4
C
C
D
N
发现:∠1+∠2= ∠AOB= 180° , ∠3+∠4 =∠CDE= 90°
一、余角和补角的概念
互为余角:如果两个角的和等于90°(直角),就说这两个角互为余角,其中一个角是另一个角的余角。
互为补角:如果两个角的和等于180°(平角),就说这两个角互为补角,其中一个角是另一个角的补角。
(1)定义中的“互为”一词如何理解?
(2)互补、互余的两角是否一定有公共顶点或公共边?
(3)∠1和∠2互补,除用符号语言表示为∠1+∠2= 180°外,用符号语言还可以表示为 ∠1= 180°- ∠2或∠2= 180°- ∠1
二、提问答疑,理解定义
(3) 30°的余角是_____,补角是______;若一个角的度数是x,
则它的余角的度数和补角的度数分别是__________,_________.
(1)若∠1与∠2互补,则∠1+ ∠2=________.
(2) ∠1= 180°- ∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
90°- x
180°- x
1、抢答
三、反馈练习
角α α的余角 α的补角
5°
42°
62°23`
78°23`8``
48°
85°
175°
138°
27°37`
117°37`
11°36`52``
101°36`52``
2、比一比,看谁最快。
(1)图中互余的角是__________与___________.
(2)图中互补的角是_______与_______;_______与______.
(3)图中相等的角是________与_________.
A
C
O
B
D
∠AOD
∠DOC
∠AOD
∠BOD
∠AOC
∠BOC
∠AOC
∠BOC
3、看图回答:
已知∠1+∠2= 180°,∠3 +∠4= 180°。若∠1=∠3,说说∠2和∠4有什么关系?
由∠1与∠2互补,∴ ∠2= 180°- ∠1
由∠3与∠4互补,∴ ∠4= 180°- ∠3
又因为∠1=∠3, 180°- ∠1=180°- ∠3
所以∠2=∠4
推导性质
1
2
3
4
解:设这个角为x度,根据题意,得:
等角 的补角相等。
归纳
等角 的余角相等。
对于补角是否也有类似性质?
一个角的补角是它的3倍,这个角是多少度?
(同角)
(同角)
练习
归纳总结
互余的角 互补的角
数量关系:
∠1+∠2= 90°
∠1+∠2= 180°
对应图形:
2
1
2
1
性质:
等角(同角)的余角相等
等角(同角)的补角相等
1
2
180°
90°
2
1
谢谢欣赏
2.7 角的和与差
A
C
B
O
图中共有几个角?
它们之间有什么关系?
图中∠AOC是∠AOB
和∠BOC的和,记作
∠AOC=∠AOB+∠BOC
图中∠AOB是∠AOC和∠BOC的差,
记作∠AOB=∠AOC-∠BOC
那么,图中∠AOC-∠AOB=
∠BOC
认识角的和差
C
B
O
A
如图(1)若∠AOC=32 ° ,∠BOC=43° 则∠AOB= ____
若已知 ∠AOB = 68 ° ∠BOC=40°
则∠AOC=____
75 °
28 °
23°31′25″
42°37′56″
42°37′56″
23°31′25″
66°9′21″
19°6′31″
O
B
A
C
∠AOC =∠BOC=
∠AOB =2∠AOC =2∠BOC
角平分线
∠AOB
从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的角平分线。
A
B
C
D
O
如图 ∠AOB=∠BOC=∠COD,
则OB 是 的平分线,
= ∠AOC,
= ∠BOD
∠BOC =
= `
AOC
BOC
BOC
AOD
BOD
AOD
此时OB、OC叫∠ AOD的三等份线
练一练
如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
D
C
B
A
O
∠AOC =∠____ + ∠ __
∠AOC= ∠____-∠ __
∠BOD - ∠COD= ∠ __
∠BOC= ∠AOC - ∠ __ = ∠BOD - ∠ __
∠AOB= ∠____ - ∠____ - ∠____
∠AOD = ∠____+ ∠ __+ ∠____
BOC
BOC
AOB
DOC
AOD
AOB
COD
AOD
BOC
COD
AOB
BOC
COD
填空
例
。
C
O
A
B
1、如图(1),若∠AOC=60°21′, ∠BOC=25°38′, 则∠AOB=____
A
O
B
C
2、如图(2),已知OB为∠AOC的平分线,∠AOC=82°16′,则∠COB=____
O
C
B
A
课堂检测
3、如图,∠AOC和∠BOD都是直角∠DOC=28°,求∠AOB的度数。
A
B
C
D
O
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB,求∠EOF的大小?
思考:
解:
∵ OE平分 ∠ AOC,OF平分 ∠COB
∴∠EOF=∠EOC+∠COF
=1/2∠AOC+1/2∠COB
=1/2(∠AOC+∠COB)
=90°
∴∠EOC=1/2∠AOC,
∠COF=1/2∠COB
(角平分线的定义)
∵∠AOB=∠AOC+∠COB=180°
(平角的定义)
A
B
E
C
F
O
思考
如图,OC平分∠AOD,∠BOD=2∠AOB.若∠AOD=114°,
求∠BOC的度数?
A
B
C
D
O
解:∵∠AOD=∠AOB+∠BOD=114°
∴∠AOB=1/3∠AOD=38°
∵OC平分∠AOD
∴∠AOC=1/2∠AOD=57°
(角平分线的定义)
∴∠BOC=∠AOC-∠AOB
∠BOD=2∠AOB
=57°-38°
=19°
解:
例
你能用三角板拼出一些特殊角吗?
利用三角尺还可以画出哪些度数的角?
30°、45°、60°、90°、15°、75°、105°、120°、135°、150°、 180°
(15的整数倍)
探究:
75°
15°
4
画出一个平角∠AOB,画一个直角∠CDE,并标出这两个角的度数,然后过这个角的顶点任意画一条射线OM和ON,并记为∠AOM=∠1,∠BOM=∠2,∠CDN=∠3,∠EDN=∠4。观察这两个角个图形有什么发现。
2
1
M
180°
90°
C
E
N
3
A
B
O
·
·
·
D
动动手,画一画。
90°
E
N
D
3
画出一个平角∠AOB,画一个直角∠CDE,并标出这两个角的度数,然后过这个角的顶点任意画一条射线OM和ON,并记为∠AOM=∠1,∠BOM=∠2,∠CEN=∠3,∠EDN=∠4。观察这两用角个图形有什么发现。
探 究
1
B
O
M
·
·
180°
A
O
M
2
4
C
C
D
N
发现:∠1+∠2= ∠AOB= 180° , ∠3+∠4 =∠CDE= 90°
一、余角和补角的概念
互为余角:如果两个角的和等于90°(直角),就说这两个角互为余角,其中一个角是另一个角的余角。
互为补角:如果两个角的和等于180°(平角),就说这两个角互为补角,其中一个角是另一个角的补角。
(1)定义中的“互为”一词如何理解?
(2)互补、互余的两角是否一定有公共顶点或公共边?
(3)∠1和∠2互补,除用符号语言表示为∠1+∠2= 180°外,用符号语言还可以表示为 ∠1= 180°- ∠2或∠2= 180°- ∠1
二、提问答疑,理解定义
(3) 30°的余角是_____,补角是______;若一个角的度数是x,
则它的余角的度数和补角的度数分别是__________,_________.
(1)若∠1与∠2互补,则∠1+ ∠2=________.
(2) ∠1= 180°- ∠2,则∠1与∠2的关系为___________.
180°
互为补角
60°
150°
90°- x
180°- x
1、抢答
三、反馈练习
角α α的余角 α的补角
5°
42°
62°23`
78°23`8``
48°
85°
175°
138°
27°37`
117°37`
11°36`52``
101°36`52``
2、比一比,看谁最快。
(1)图中互余的角是__________与___________.
(2)图中互补的角是_______与_______;_______与______.
(3)图中相等的角是________与_________.
A
C
O
B
D
∠AOD
∠DOC
∠AOD
∠BOD
∠AOC
∠BOC
∠AOC
∠BOC
3、看图回答:
已知∠1+∠2= 180°,∠3 +∠4= 180°。若∠1=∠3,说说∠2和∠4有什么关系?
由∠1与∠2互补,∴ ∠2= 180°- ∠1
由∠3与∠4互补,∴ ∠4= 180°- ∠3
又因为∠1=∠3, 180°- ∠1=180°- ∠3
所以∠2=∠4
推导性质
1
2
3
4
解:设这个角为x度,根据题意,得:
等角 的补角相等。
归纳
等角 的余角相等。
对于补角是否也有类似性质?
一个角的补角是它的3倍,这个角是多少度?
(同角)
(同角)
练习
归纳总结
互余的角 互补的角
数量关系:
∠1+∠2= 90°
∠1+∠2= 180°
对应图形:
2
1
2
1
性质:
等角(同角)的余角相等
等角(同角)的补角相等
1
2
180°
90°
2
1
谢谢欣赏
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
