冀教版七年级上册数学 2.8平面图形的旋转 课件(共24张)
文档属性
| 名称 | 冀教版七年级上册数学 2.8平面图形的旋转 课件(共24张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 710.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
2.8 平面图形的旋转
旋转木马
旋转飞机
动动脑筋:以上这些转运动有什么共同的特征?
这个定点O
称为旋转中心
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
P
o
转动的角∠POP
称为旋转角
P
′
′
实验步骤:
1、把老师给的三角形紧压在一张白纸上,用笔沿着三角形的外边缘线画三角形△AOB。
2、用图钉将(O)固定,将纸片绕着(O)转动,纸片上的三角形就旋转到了新的位置.
3、再沿着三角形的外边缘线画三角形△ AOB 。
动手实验
′
′
思考:
1、旋转中心是什么
2、沿着顺时针还是逆时针方向旋转
3、旋转了多少度,可以通过量角器测量得到
概括总结
从刚才所完成的实验中:
1、你认为决定图形旋转的主要因素是什么?
2、旋转的过程中,旋转中心发生变化了吗?
3、图形旋转的过程中,如何确定图形旋转的角度?
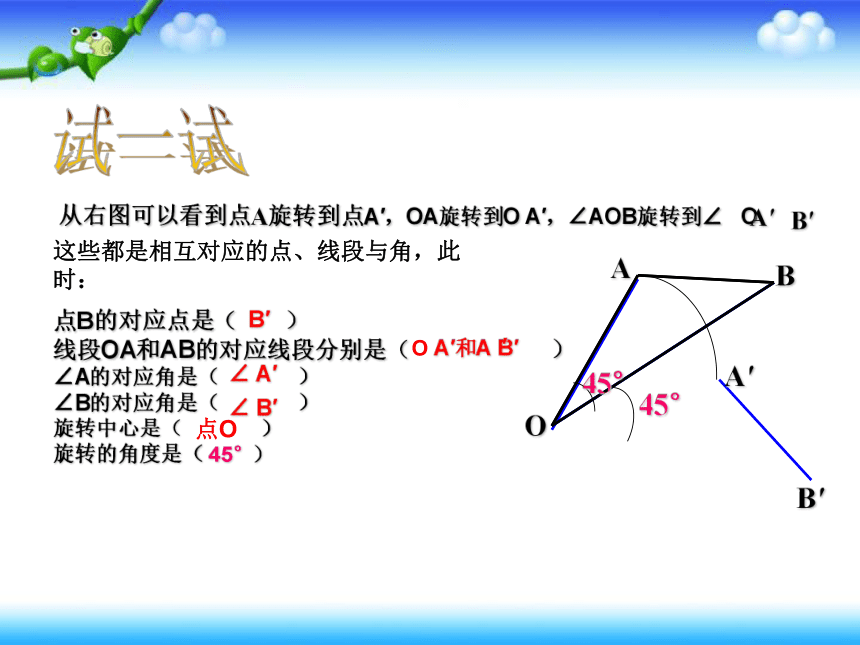
从右图可以看到点A旋转到点A′,OA旋转到O A′,∠AOB旋转到∠ O
O
A
B
A′
B′
45°
45°
点B的对应点是( )
线段OA和AB的对应线段分别是( )
∠A的对应角是( )
∠B的对应角是( )
旋转中心是( )
旋转的角度是( )
A′
B′
这些都是相互对应的点、线段与角,此时:
B′
O A′和A B′
′
∠ A′
∠ B′
点O
45°
试一试
动态演示
O
P′
P
钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心是( )
(2)经过20分钟,分针旋转了( )度?
想一想
点O
120
如图,如果把四边形AOBC绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是( )。
⑵经过旋转,点A和点B分别移动到( )的位置。
⑶旋转角是( )。
⑷AO与DO的长度关系是( )。
⑸∠AOD与∠BOE的
大小关系是( )
旋转中心是O
点D和点E
AO=DO;BO=EO
∠AOD=∠BOE
∠AOD和∠BOE
B
A
C
O
D
E
F
0
A
B
C
·
A′
B′
C′
90°
做一做
如图,如果旋转中心在△ABC的外面点O处,逆时针转动90°,将整个△ABC旋转到△ ABC 的位置,那么这两个三角形的顶点、边与角是如何对应的呢?
′
′
′
简单的旋转作图
项目 已知 未知 备注
原图形 ● 点A
原位置 ● 点A
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 点
目标位置 ● 点B (求作)
A
O
点的旋转作法
例1 将A点绕O点沿
顺时针方向旋转60 .
分析:
作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.
B
项目 已知 未知 备注
原图形 ● 线段AB
原位置 ● 线段AB
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 线段
目标位置 ● 线段CD (求作)
A
O
线段的旋转作法
例2 将线段AB绕O点沿顺时针方向旋转60 .
分析:
作法:
将点A绕点O顺时针旋转60 ,得
点C;
2. 将点B绕点O顺时针旋转60 ,得点D ;
3. 连接CD, 则线段CD即为所求作.
C
B
D
项目 已知 未知 备注
原图形 ● △ABC
原位置 ● △ABC
旋转中心 ● 点C
旋转方向 ● 根据A与D的对应关系判断为顺时针
旋转角度 ● ∠ACD
目标图形 ● 三角形
目标位置 ● △DEC (求作)
例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.
分析:
作法二:
1. 连接CD;
2. 以C为圆心,CB长为半径画圆 ;
3. 延长CA,交⊙C与M,延长CD,交⊙C与N;
4. 在⊙C上截取BE=MN,则E点为B点的
对应点;
5. 连接CE, DE,则△DEC即为所求作.
C
A
B
D
E
M
N
还有其它作法吗?
开始
旋转要素分析
控制点选择
控制点旋转
旋转后控制点连线
(旋转后作图)
结束
有时,旋转中心以及旋转方向与角度不是显式告知的,需要化未知为已知.
线段的端点、多边形顶点、折线的连接点、线段与曲线的连接点、圆或圆弧或扇形的圆心.
注意连接顺序,有时需要用圆规进行作图(根据圆心控制点以及已知半径).
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90 ,作出旋转后的图案.
旋转作图除了要知道待平移图形的大小、形状和位置外,还需要旋转中心、旋转方向和旋转角度三个要素;
旋转中心、旋转方向与旋转角度有时需要根据旋转的性质化未知为已知;
点和线段的旋转根据旋转的定义与性质实现作图;
一般图形的旋转首先通过选取若干个控制点化归为点和线段的旋转;然后运用旋转的性质进行作图.
点的旋转作法:以旋转中心为圆心,旋 转 中心到待旋转点的距离为 半径画圆,连接旋转中心到待旋转点的半径,过旋 转中心按指定方向作另一 半径,使与前一半径的夹 角等于已知角,该半径交于圆上的点即为所求作.
线段的旋转作法:将线段两端点分别旋转,然后将两个旋转后 的点连成线段,即为原 线段旋转后的线段.
总结:
例1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
研讨应用
解 (1)旋转中心是点A.
(3)点M 转到了AC的中点位置上
(2)旋转了60
例2、如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
研讨应用
例3、如图11.2.7(1)点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢?
研讨应用
每组图形中的一个,是怎样旋转变换成另一个的?
A
C
E
B
D
A
C
B
D
E
两个直角三角形
两个等腰直角三角形
通过本节课的学习,请你来谈谈你的收获吧!
一、这节课老师教给了你们什么?
二、这节课学到了些什么?
三、你们还有什么疑问需要老师给你们解决?
谢谢欣赏
2.8 平面图形的旋转
旋转木马
旋转飞机
动动脑筋:以上这些转运动有什么共同的特征?
这个定点O
称为旋转中心
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
P
o
转动的角∠POP
称为旋转角
P
′
′
实验步骤:
1、把老师给的三角形紧压在一张白纸上,用笔沿着三角形的外边缘线画三角形△AOB。
2、用图钉将(O)固定,将纸片绕着(O)转动,纸片上的三角形就旋转到了新的位置.
3、再沿着三角形的外边缘线画三角形△ AOB 。
动手实验
′
′
思考:
1、旋转中心是什么
2、沿着顺时针还是逆时针方向旋转
3、旋转了多少度,可以通过量角器测量得到
概括总结
从刚才所完成的实验中:
1、你认为决定图形旋转的主要因素是什么?
2、旋转的过程中,旋转中心发生变化了吗?
3、图形旋转的过程中,如何确定图形旋转的角度?
从右图可以看到点A旋转到点A′,OA旋转到O A′,∠AOB旋转到∠ O
O
A
B
A′
B′
45°
45°
点B的对应点是( )
线段OA和AB的对应线段分别是( )
∠A的对应角是( )
∠B的对应角是( )
旋转中心是( )
旋转的角度是( )
A′
B′
这些都是相互对应的点、线段与角,此时:
B′
O A′和A B′
′
∠ A′
∠ B′
点O
45°
试一试
动态演示
O
P′
P
钟表的分针匀速旋转一周需要60分钟.
(1)指出它的旋转中心是( )
(2)经过20分钟,分针旋转了( )度?
想一想
点O
120
如图,如果把四边形AOBC绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是( )。
⑵经过旋转,点A和点B分别移动到( )的位置。
⑶旋转角是( )。
⑷AO与DO的长度关系是( )。
⑸∠AOD与∠BOE的
大小关系是( )
旋转中心是O
点D和点E
AO=DO;BO=EO
∠AOD=∠BOE
∠AOD和∠BOE
B
A
C
O
D
E
F
0
A
B
C
·
A′
B′
C′
90°
做一做
如图,如果旋转中心在△ABC的外面点O处,逆时针转动90°,将整个△ABC旋转到△ ABC 的位置,那么这两个三角形的顶点、边与角是如何对应的呢?
′
′
′
简单的旋转作图
项目 已知 未知 备注
原图形 ● 点A
原位置 ● 点A
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 点
目标位置 ● 点B (求作)
A
O
点的旋转作法
例1 将A点绕O点沿
顺时针方向旋转60 .
分析:
作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.
B
项目 已知 未知 备注
原图形 ● 线段AB
原位置 ● 线段AB
旋转中心 ● 点O
旋转方向 ● 顺时针
旋转角度 ● 60
目标图形 ● 线段
目标位置 ● 线段CD (求作)
A
O
线段的旋转作法
例2 将线段AB绕O点沿顺时针方向旋转60 .
分析:
作法:
将点A绕点O顺时针旋转60 ,得
点C;
2. 将点B绕点O顺时针旋转60 ,得点D ;
3. 连接CD, 则线段CD即为所求作.
C
B
D
项目 已知 未知 备注
原图形 ● △ABC
原位置 ● △ABC
旋转中心 ● 点C
旋转方向 ● 根据A与D的对应关系判断为顺时针
旋转角度 ● ∠ACD
目标图形 ● 三角形
目标位置 ● △DEC (求作)
例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.
分析:
作法二:
1. 连接CD;
2. 以C为圆心,CB长为半径画圆 ;
3. 延长CA,交⊙C与M,延长CD,交⊙C与N;
4. 在⊙C上截取BE=MN,则E点为B点的
对应点;
5. 连接CE, DE,则△DEC即为所求作.
C
A
B
D
E
M
N
还有其它作法吗?
开始
旋转要素分析
控制点选择
控制点旋转
旋转后控制点连线
(旋转后作图)
结束
有时,旋转中心以及旋转方向与角度不是显式告知的,需要化未知为已知.
线段的端点、多边形顶点、折线的连接点、线段与曲线的连接点、圆或圆弧或扇形的圆心.
注意连接顺序,有时需要用圆规进行作图(根据圆心控制点以及已知半径).
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90 ,作出旋转后的图案.
旋转作图除了要知道待平移图形的大小、形状和位置外,还需要旋转中心、旋转方向和旋转角度三个要素;
旋转中心、旋转方向与旋转角度有时需要根据旋转的性质化未知为已知;
点和线段的旋转根据旋转的定义与性质实现作图;
一般图形的旋转首先通过选取若干个控制点化归为点和线段的旋转;然后运用旋转的性质进行作图.
点的旋转作法:以旋转中心为圆心,旋 转 中心到待旋转点的距离为 半径画圆,连接旋转中心到待旋转点的半径,过旋 转中心按指定方向作另一 半径,使与前一半径的夹 角等于已知角,该半径交于圆上的点即为所求作.
线段的旋转作法:将线段两端点分别旋转,然后将两个旋转后 的点连成线段,即为原 线段旋转后的线段.
总结:
例1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
研讨应用
解 (1)旋转中心是点A.
(3)点M 转到了AC的中点位置上
(2)旋转了60
例2、如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
研讨应用
例3、如图11.2.7(1)点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90,旋转后的线段与原线段的位置有何关系?,如果逆时针方向旋转90呢?
研讨应用
每组图形中的一个,是怎样旋转变换成另一个的?
A
C
E
B
D
A
C
B
D
E
两个直角三角形
两个等腰直角三角形
通过本节课的学习,请你来谈谈你的收获吧!
一、这节课老师教给了你们什么?
二、这节课学到了些什么?
三、你们还有什么疑问需要老师给你们解决?
谢谢欣赏
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
