15.1.1.4整式的乘法(3)
文档属性
| 名称 | 15.1.1.4整式的乘法(3) |  | |
| 格式 | zip | ||
| 文件大小 | 594.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-06 10:13:25 | ||
图片预览






文档简介
课件16张PPT。第十五章 整式的乘除与因式分解15.1.4 整式的乘法(3)多项式乘以多项式丰润区第三中学 (1) (-3x2) 2xy(2) 2a(3ab-b+1)(4) (2x-5y)(3x+y)计算:6a2b-2ab+2a -6x3y做一做思考:上述前3个问题中,涉及到我们学过的那些运算法则?
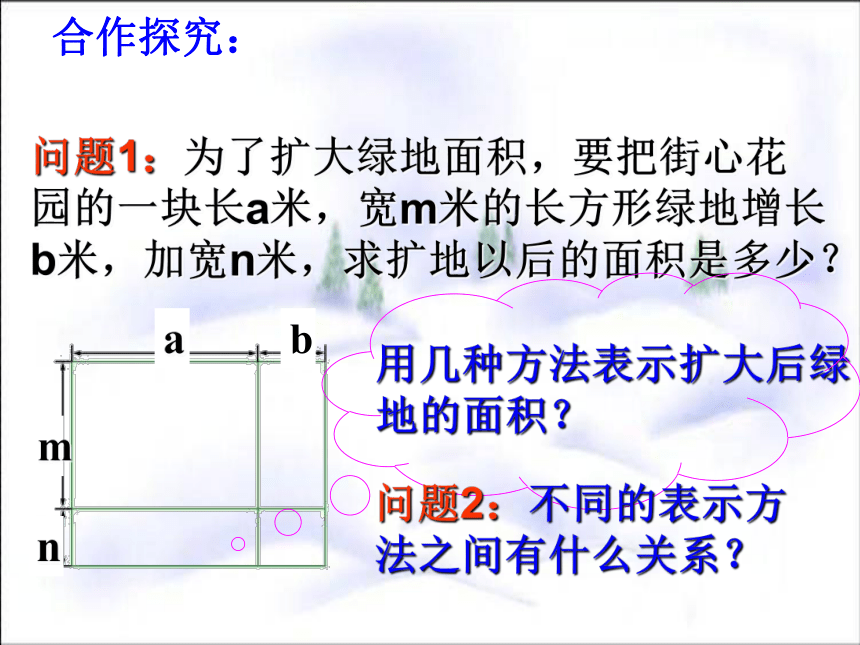
对于第(4)问题我们用以前学过的运算法则能够解决这个问题吗?知识回顾:·(3) (x-2y)(-2x2)-2x3+4x2y问题1:为了扩大绿地面积,要把街心花园的一块长a米,宽m米的长方形绿地增长b米,加宽n米,求扩地以后的面积是多少?合作探究:问题2:不同的表示方法之间有什么关系?
方法四:这块花园是由上两块和下两块组成 面积为 m(a+b)+n(a+b)米2.方法三:这块花园是由前两块和后两块组成 面积为 a(m+n)+b(m+n)米2方法二:这块花园现在是由四小块组成,它们的面积分别为:am米2、an米2、bm米2、bn米2,故这块绿地的面积为(am+an+bm+bn)米2.方法一:这块花园现在长(a+b)米,宽(m+n)米,因而面积为(a+b)(m+n)米2. ∵这四种方法表示同一块绿地的面积,∴(a+b)(m+n)=am+an+bm+bn
合作探究:问题3:上面的问题,我们从面积的角度得出了一些等式,下面你能不能尝试从代数运算的角度解释等式的合理性. =am+an+bm+bn 或∴ (a+b)(m+n)=a(m+n)+b(m+n)
=am+an+bm+bn
(a+b)(m+n)=m(a+b)+n(a+b)新知探究:(a+b)(m+n)=am+an+bm+bn(a+b)(m+n)=a(m+n)+b(m+n) ----单×多=am+an+bm+bn ----单×单总体上看,(a+b)(m+n)的结果可以看作由a+b得每一项乘m+n的每一项,再把所得的积相加而得到,即
多项式与多项式相乘的运算法则: 多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
未合并同类项之前多项式与多项式的积的项数等于两个多项式的项数之积吗?新知学习:拓展:(a+b+c)(m+n) =am+an+bm+bn+cm+cn问题5:例:计算(3x+1)(x+2) (2) (x-8y)(x-y)
(3)(x+y)(x2-xy+y2)解:(1)原式=(3x) ·x+(3x) ·2+1·x+1·2=3x2+6x+x+2= 3x2+7x+2(2)原式=x2-xy-8xy+8y2= x2﹣9xy+8y2(3)原式=x3-x2y+xy2+x2y-xy2+y3=x3+y3新知应用: (1).多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。
问题7 解题时应注意什么问题?(2).最后的结果要合并同类项.
解: (1)原式 = 2x2+6x+x+3 = 2x2+7x+3 (2)原式=m2-3mn+2mn-6n2=m2-mn-6n2 (3)原式=(a-1)(a-1) =a2-a-a+1
=a2-2a+1新知巩固:计算:(1)(2x+1)(x+3) (2) (m+2n)(m-3n)
(3) (a-1)2 解: (4)原式=a2-3ab+3ab-9b2
=a2-9b2(5)原式=2x3-8x2-x+4(6)原式=2x3-5x2+6x-15(4) (a+3b)(a-3b) (5) (2x2-1)(x-4)
(6) (x2+3)(2x-5)计算:探索规律:计算:
由上面计算的结果找规律,观察右图填空:(x+p)(x+q)
=( ) 2+( )x+( )口答: (x-7)(x+5) =x2+( )x+( )
xp+qpq-2-35 (3) (y+4)(y-2) (4)(y-5)(y-3)
(1)(x+2)(x+3) (2) (x-4)(x+1)
xpxqx2qxpxpq答案(1) x2+5x+6 (2) x2-3x-4(3) y2+2y-8 (4) y2-8y+15
中考链接:(1) (2011年 宁夏)
已知:a+b=3/2 ,ab=1 化简(a-2)(b-2)的结果是( )
(2) (2011年 北京)已知 :x2-5x=14 求:
(x-1)(2x-1)-(x+1) 2+1的值
解:原式=2x2-3x+1-(x2+2x+1)+1
=2x2-3x+1-x2-2x-1+1
=x2-5x+1
将x2-5x=14代入原式 =14+1=15。2能力挑战归纳小结谈谈你这节课的收获!!你讲我说共交流多项式乘以多项式法则: 1.多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。 注意:
1、必须做到不重复,不遗漏;2、注意确定积中每一项的符号;
3、最后结果应合并同类项。
作业 1.课本149页5题、6题、7题、10题
2 .预习 15.2.1乘法公式
对于第(4)问题我们用以前学过的运算法则能够解决这个问题吗?知识回顾:·(3) (x-2y)(-2x2)-2x3+4x2y问题1:为了扩大绿地面积,要把街心花园的一块长a米,宽m米的长方形绿地增长b米,加宽n米,求扩地以后的面积是多少?合作探究:问题2:不同的表示方法之间有什么关系?
方法四:这块花园是由上两块和下两块组成 面积为 m(a+b)+n(a+b)米2.方法三:这块花园是由前两块和后两块组成 面积为 a(m+n)+b(m+n)米2方法二:这块花园现在是由四小块组成,它们的面积分别为:am米2、an米2、bm米2、bn米2,故这块绿地的面积为(am+an+bm+bn)米2.方法一:这块花园现在长(a+b)米,宽(m+n)米,因而面积为(a+b)(m+n)米2. ∵这四种方法表示同一块绿地的面积,∴(a+b)(m+n)=am+an+bm+bn
合作探究:问题3:上面的问题,我们从面积的角度得出了一些等式,下面你能不能尝试从代数运算的角度解释等式的合理性. =am+an+bm+bn 或∴ (a+b)(m+n)=a(m+n)+b(m+n)
=am+an+bm+bn
(a+b)(m+n)=m(a+b)+n(a+b)新知探究:(a+b)(m+n)=am+an+bm+bn(a+b)(m+n)=a(m+n)+b(m+n) ----单×多=am+an+bm+bn ----单×单总体上看,(a+b)(m+n)的结果可以看作由a+b得每一项乘m+n的每一项,再把所得的积相加而得到,即
多项式与多项式相乘的运算法则: 多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
未合并同类项之前多项式与多项式的积的项数等于两个多项式的项数之积吗?新知学习:拓展:(a+b+c)(m+n) =am+an+bm+bn+cm+cn问题5:例:计算(3x+1)(x+2) (2) (x-8y)(x-y)
(3)(x+y)(x2-xy+y2)解:(1)原式=(3x) ·x+(3x) ·2+1·x+1·2=3x2+6x+x+2= 3x2+7x+2(2)原式=x2-xy-8xy+8y2= x2﹣9xy+8y2(3)原式=x3-x2y+xy2+x2y-xy2+y3=x3+y3新知应用: (1).多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。
问题7 解题时应注意什么问题?(2).最后的结果要合并同类项.
解: (1)原式 = 2x2+6x+x+3 = 2x2+7x+3 (2)原式=m2-3mn+2mn-6n2=m2-mn-6n2 (3)原式=(a-1)(a-1) =a2-a-a+1
=a2-2a+1新知巩固:计算:(1)(2x+1)(x+3) (2) (m+2n)(m-3n)
(3) (a-1)2 解: (4)原式=a2-3ab+3ab-9b2
=a2-9b2(5)原式=2x3-8x2-x+4(6)原式=2x3-5x2+6x-15(4) (a+3b)(a-3b) (5) (2x2-1)(x-4)
(6) (x2+3)(2x-5)计算:探索规律:计算:
由上面计算的结果找规律,观察右图填空:(x+p)(x+q)
=( ) 2+( )x+( )口答: (x-7)(x+5) =x2+( )x+( )
xp+qpq-2-35 (3) (y+4)(y-2) (4)(y-5)(y-3)
(1)(x+2)(x+3) (2) (x-4)(x+1)
xpxqx2qxpxpq答案(1) x2+5x+6 (2) x2-3x-4(3) y2+2y-8 (4) y2-8y+15
中考链接:(1) (2011年 宁夏)
已知:a+b=3/2 ,ab=1 化简(a-2)(b-2)的结果是( )
(2) (2011年 北京)已知 :x2-5x=14 求:
(x-1)(2x-1)-(x+1) 2+1的值
解:原式=2x2-3x+1-(x2+2x+1)+1
=2x2-3x+1-x2-2x-1+1
=x2-5x+1
将x2-5x=14代入原式 =14+1=15。2能力挑战归纳小结谈谈你这节课的收获!!你讲我说共交流多项式乘以多项式法则: 1.多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。 注意:
1、必须做到不重复,不遗漏;2、注意确定积中每一项的符号;
3、最后结果应合并同类项。
作业 1.课本149页5题、6题、7题、10题
2 .预习 15.2.1乘法公式
