沪科版数学八年级下19.1.2多边形内角和 课件(共23张PPT)
文档属性
| 名称 | 沪科版数学八年级下19.1.2多边形内角和 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 21:36:17 | ||
图片预览






文档简介
(共23张PPT)
沪科版数学八年级下册
第19章 四边形
19.1 多边形的内角和
第2课时 多边形外角和
教学目标
n边形的内角和为 。
n边形从一个顶点出发的对角线有 条
n边形共有对角线 条
(n-3) (n≥3)
n(n-3) (n≥3)
(n-2) ×180°(n≥3)
知识回顾
知识回顾
2、一个内角和为1620°的多边形有多少条对角线
1、在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80o
解: 设这个多边形的边数为n,得:
(n-2) 180°= 1620
解得:n=11
n(n-3)= ×11×(11-3)=44(条)
答:这个多边形有44条对角线
新知导入
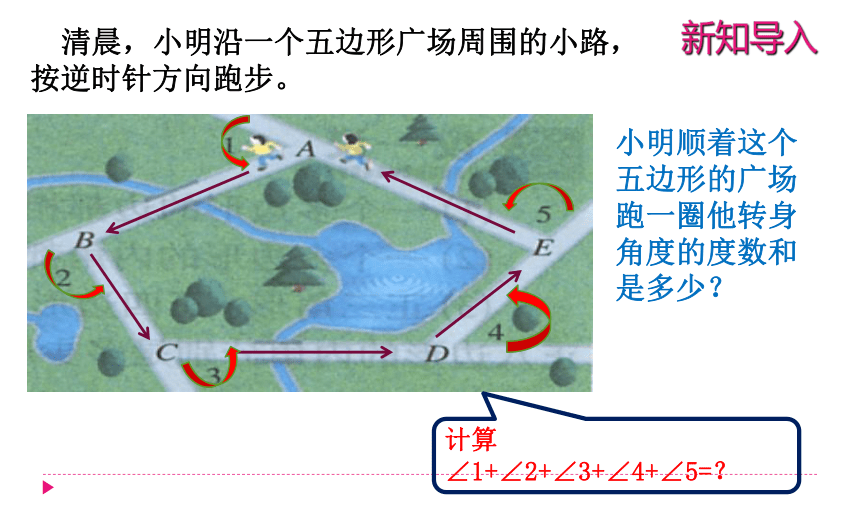
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
小明顺着这个五边形的广场跑一圈他转身角度的度数和是多少?
计算
∠1+∠2+∠3+∠4+∠5=?
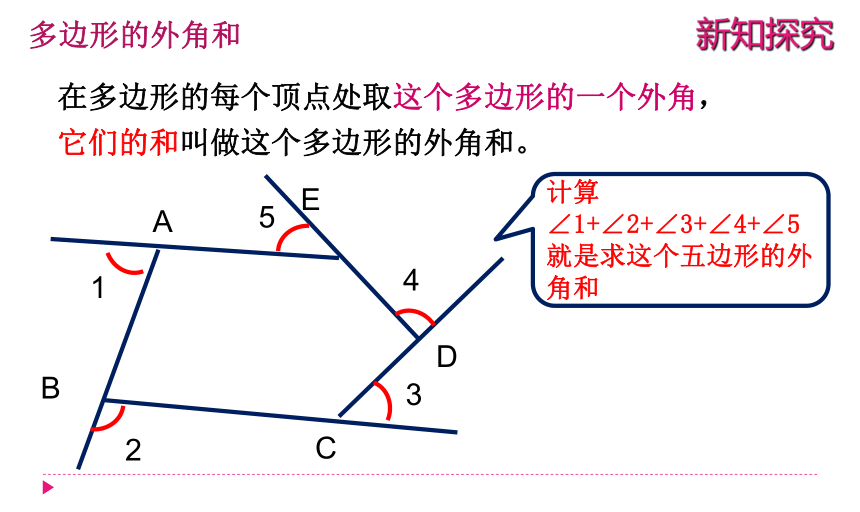
在多边形的每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
多边形的外角和
计算
∠1+∠2+∠3+∠4+∠5就是求这个五边形的外角和
A
B
C
E
4
D
1
2
3
5
新知探究
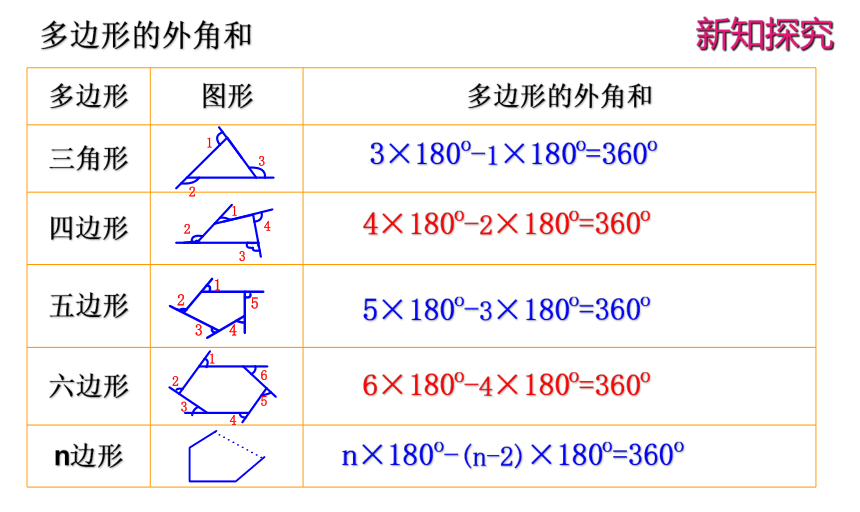
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-1×180o=360o
4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
n×180o-(n-2)×180o=360o
多边形的外角和
新知探究
n边形的内角和与外角和之和构成n个平角.
即:内角和+外角和=n×180°
内角和=(n-2)× 180°
∴ 外角和= n×180° -(n-2)× 180°
=360°
定理 、
n边形的外角和等于360°(n为不小于3的整数).
新知讲解
例1 一个正多边形的内角和等于它的外角和的3倍,求它是几边形?
解: 设这个多边形的边数为n,则它的内角和等于 (n-2) 180°,
(n-2) 180°= 3×360
n = 8
这个多边形的边数为8.
例题讲解
答:它是八边形
变式练习:一个正多边形的内角和等于它的外角和的3倍,求它的每个内角度数
解: 设这个多边形的边数为n,则它的内角和等于 (n-2) 180°,
(n-2) 180°= 3×360
n = 8
这个多边形的边数为8.
∴ 180°-360 ÷8=135°
答:它的每个内角度度数是135°
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
例题讲解
为什么房顶钢架要做成三角形?
新知探究
三角形具有稳定性
三角形具有稳定性
三角形的三边确定,三角形的形状和大小也就被确定,形状、大小唯一
为什么这些要选四边形呢?
活动:四根小棒(2长2短)摆四边形.看看你分别有多少种不同的摆法?
与三角形的稳定性相反,四边形具有不稳定性
新知探究
四边形的不稳定性
四边形具有不稳定性,实质是指四边形边长确定,其形状、大小不能完全确定.
正是由于四边形具有不稳定性,可以变动,所以它可以拉开,也可以收拢,在实际生活中有很多应用
电力伸缩门
放缩尺
可折叠多功能衣架
折叠椅
折叠伞蓬骨架
升降机
新知练习
1、一个多边形的内角和等于1440°,那么它是______边形。
2、正五边形的每一个内角的度数是_______。
十
108°
3、正n边形的一个外角与一个内角的比是2:3,这个正n边形的内角和是 .
540°
4、一个多边形除去一个角后的内角和等于1020°,
它是 边形
八
5、一个多边形的内角和与外角和相等,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
6、如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
7、如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
A.120° B.180° C.240° D.300°
A
D
D
1
2
60°
C
1、一个六边形如图,已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数。
A
B
C
D
E
F
1
2
3
4
解:如图所示,连结AD,
∵AB∥DE, CD∥AF(已知)
∴∠1=∠3,∠2=∠4
(两直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E= 1/2 ×720°=360°
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°= 720°
思考:有没有其它的解法?
F
E
D
C
B
A
P
R
Q
3
2
1
提升练习
A
B
C
D
E
F
∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°
1
2
P
Q
R
如图所示:可向两个方向分别延长AB,CD,EF三条边,构成△PQR。
∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,
∴∠CDE=∠FAB
同理∠AFE=∠BCD,∠ABC=∠DEF
∴∠FAB+∠BCD+∠DEF= 1/2 ×720°=360°
解法二:
2、如图,点E,F,G,H在长方形ABCD的四条边上,已知∠1=∠2=300,∠3=200。求五边形FGCHE各个内角的度数。
A
H
G
F
E
D
C
B
1
3
2
提升练习
解:由题意得:
∠A= ∠C =∠D=90°
∵∠1=∠2=30°,
∴∠QEH=∠EFA=600
∴∠FEH=180°-30°-60°=90°
∵ ∠3=200
∴∠EFG=180°-20°-60°=100°
∵∠1+∠CHE=180°
∴∠CHE=180°-30°=150°
∴∠CGF=(5-3)×180°-90°-90°-100°-150°=100°
拓展练习
(1)如图甲,以 ABC的各个顶点为圆心,2cm 为半径画三个圆,则圆与 ABC的公共部分的面积和为_______.
甲
A
B
C
乙
A
C
D
B
丙
B
A
D
C
E
(2)如图乙,以四边形ABCD的各个顶点为圆心,2cm为半径画四个圆,则圆与四边形ABCD的公共部分的面积和为_______.
(3)如图丙,以五边形ABCDE的各个顶点为圆心,2cm为半径画五个圆,则圆与五边形ABCE的公共部分的面积和为_______.
4π
6π
2π
(1)已知边数如何求内角和。
(2)已知内角和如何求边数。
n边形内角和等于(n -2)180°(n≥3)。
n边形的外角和等于360°。
n边形的对角线条数= (n≥3)。
说说这节课的收获和体验.
课堂小结
沪科版数学八年级下册
第19章 四边形
19.1 多边形的内角和
第2课时 多边形外角和
教学目标
n边形的内角和为 。
n边形从一个顶点出发的对角线有 条
n边形共有对角线 条
(n-3) (n≥3)
n(n-3) (n≥3)
(n-2) ×180°(n≥3)
知识回顾
知识回顾
2、一个内角和为1620°的多边形有多少条对角线
1、在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80o
解: 设这个多边形的边数为n,得:
(n-2) 180°= 1620
解得:n=11
n(n-3)= ×11×(11-3)=44(条)
答:这个多边形有44条对角线
新知导入
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
小明顺着这个五边形的广场跑一圈他转身角度的度数和是多少?
计算
∠1+∠2+∠3+∠4+∠5=?
在多边形的每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和。
多边形的外角和
计算
∠1+∠2+∠3+∠4+∠5就是求这个五边形的外角和
A
B
C
E
4
D
1
2
3
5
新知探究
多边形 图形 多边形的外角和
三角形
四边形
五边形
六边形
n边形
3×180o-1×180o=360o
4×180o-2×180o=360o
5×180o-3×180o=360o
6×180o-4×180o=360o
n×180o-(n-2)×180o=360o
多边形的外角和
新知探究
n边形的内角和与外角和之和构成n个平角.
即:内角和+外角和=n×180°
内角和=(n-2)× 180°
∴ 外角和= n×180° -(n-2)× 180°
=360°
定理 、
n边形的外角和等于360°(n为不小于3的整数).
新知讲解
例1 一个正多边形的内角和等于它的外角和的3倍,求它是几边形?
解: 设这个多边形的边数为n,则它的内角和等于 (n-2) 180°,
(n-2) 180°= 3×360
n = 8
这个多边形的边数为8.
例题讲解
答:它是八边形
变式练习:一个正多边形的内角和等于它的外角和的3倍,求它的每个内角度数
解: 设这个多边形的边数为n,则它的内角和等于 (n-2) 180°,
(n-2) 180°= 3×360
n = 8
这个多边形的边数为8.
∴ 180°-360 ÷8=135°
答:它的每个内角度度数是135°
例2:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。
例题讲解
为什么房顶钢架要做成三角形?
新知探究
三角形具有稳定性
三角形具有稳定性
三角形的三边确定,三角形的形状和大小也就被确定,形状、大小唯一
为什么这些要选四边形呢?
活动:四根小棒(2长2短)摆四边形.看看你分别有多少种不同的摆法?
与三角形的稳定性相反,四边形具有不稳定性
新知探究
四边形的不稳定性
四边形具有不稳定性,实质是指四边形边长确定,其形状、大小不能完全确定.
正是由于四边形具有不稳定性,可以变动,所以它可以拉开,也可以收拢,在实际生活中有很多应用
电力伸缩门
放缩尺
可折叠多功能衣架
折叠椅
折叠伞蓬骨架
升降机
新知练习
1、一个多边形的内角和等于1440°,那么它是______边形。
2、正五边形的每一个内角的度数是_______。
十
108°
3、正n边形的一个外角与一个内角的比是2:3,这个正n边形的内角和是 .
540°
4、一个多边形除去一个角后的内角和等于1020°,
它是 边形
八
5、一个多边形的内角和与外角和相等,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
6、如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A.正三角形 B.正四边形 C.正六边形 D.正八边形
7、如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
A.120° B.180° C.240° D.300°
A
D
D
1
2
60°
C
1、一个六边形如图,已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数。
A
B
C
D
E
F
1
2
3
4
解:如图所示,连结AD,
∵AB∥DE, CD∥AF(已知)
∴∠1=∠3,∠2=∠4
(两直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E= 1/2 ×720°=360°
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°= 720°
思考:有没有其它的解法?
F
E
D
C
B
A
P
R
Q
3
2
1
提升练习
A
B
C
D
E
F
∵∠FAB+∠ABC+∠BCD+∠CDE+∠DEF+∠AFE=(6-2)×180°=720°
1
2
P
Q
R
如图所示:可向两个方向分别延长AB,CD,EF三条边,构成△PQR。
∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1=∠2,
∴∠CDE=∠FAB
同理∠AFE=∠BCD,∠ABC=∠DEF
∴∠FAB+∠BCD+∠DEF= 1/2 ×720°=360°
解法二:
2、如图,点E,F,G,H在长方形ABCD的四条边上,已知∠1=∠2=300,∠3=200。求五边形FGCHE各个内角的度数。
A
H
G
F
E
D
C
B
1
3
2
提升练习
解:由题意得:
∠A= ∠C =∠D=90°
∵∠1=∠2=30°,
∴∠QEH=∠EFA=600
∴∠FEH=180°-30°-60°=90°
∵ ∠3=200
∴∠EFG=180°-20°-60°=100°
∵∠1+∠CHE=180°
∴∠CHE=180°-30°=150°
∴∠CGF=(5-3)×180°-90°-90°-100°-150°=100°
拓展练习
(1)如图甲,以 ABC的各个顶点为圆心,2cm 为半径画三个圆,则圆与 ABC的公共部分的面积和为_______.
甲
A
B
C
乙
A
C
D
B
丙
B
A
D
C
E
(2)如图乙,以四边形ABCD的各个顶点为圆心,2cm为半径画四个圆,则圆与四边形ABCD的公共部分的面积和为_______.
(3)如图丙,以五边形ABCDE的各个顶点为圆心,2cm为半径画五个圆,则圆与五边形ABCE的公共部分的面积和为_______.
4π
6π
2π
(1)已知边数如何求内角和。
(2)已知内角和如何求边数。
n边形内角和等于(n -2)180°(n≥3)。
n边形的外角和等于360°。
n边形的对角线条数= (n≥3)。
说说这节课的收获和体验.
课堂小结
