沪科版数学八年级下19.1.1多边形内角和 (共25张PPT)
文档属性
| 名称 | 沪科版数学八年级下19.1.1多边形内角和 (共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 370.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 21:37:17 | ||
图片预览




文档简介
(共25张PPT)
沪科版数学八年级下册
第19章 四边形
19.1 多边形的内角和
第1课时 多边形及其内角和公式
教学目标
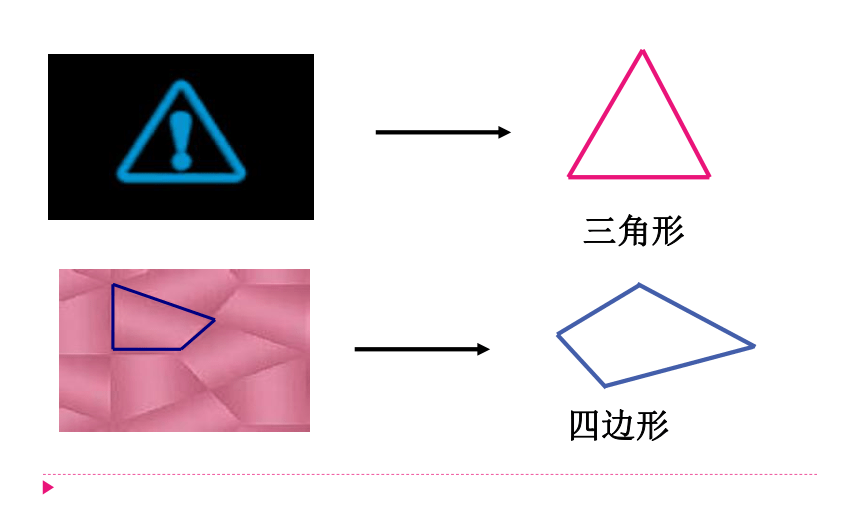
观察下列图形,由这图形你能抽象出什么几何图形?
新知导入
三角形
四边形
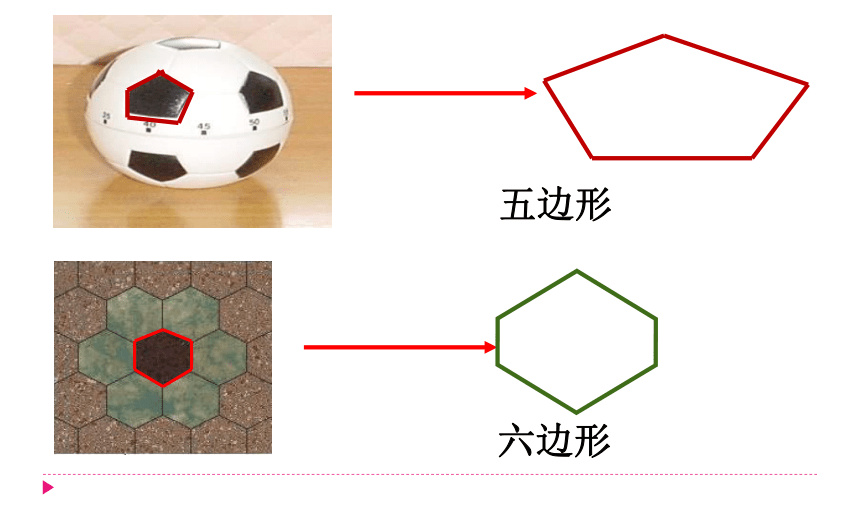
五边形
六边形
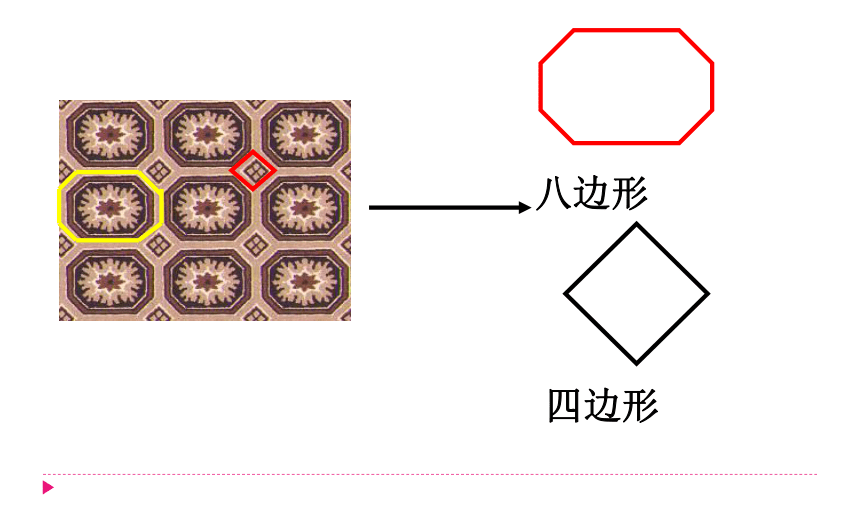
八边形
四边形
新知讲解
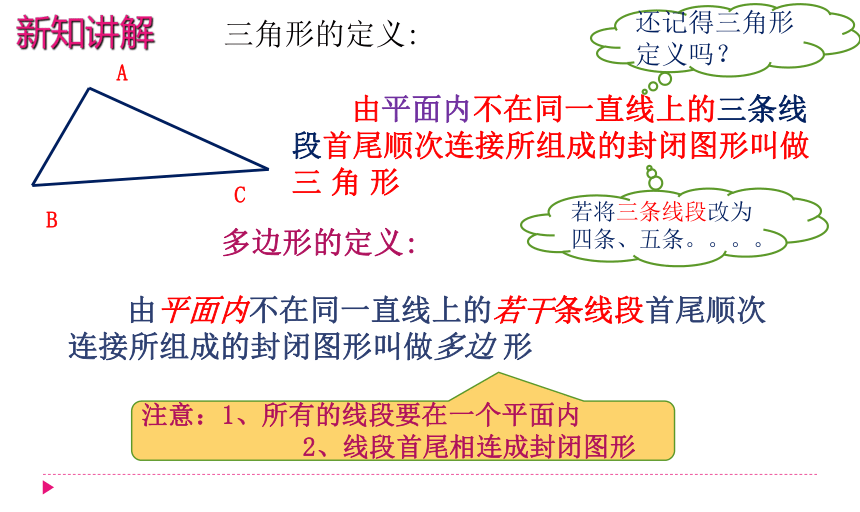
由平面内不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫做三 角 形
三角形的定义:
还记得三角形定义吗?
A
B
C
若将三条线段改为四条、五条。。。。
多边形的定义:
由平面内不在同一直线上的若干条线段首尾顺次连接所组成的封闭图形叫做多边 形
注意:1、所有的线段要在一个平面内
2、线段首尾相连成封闭图形
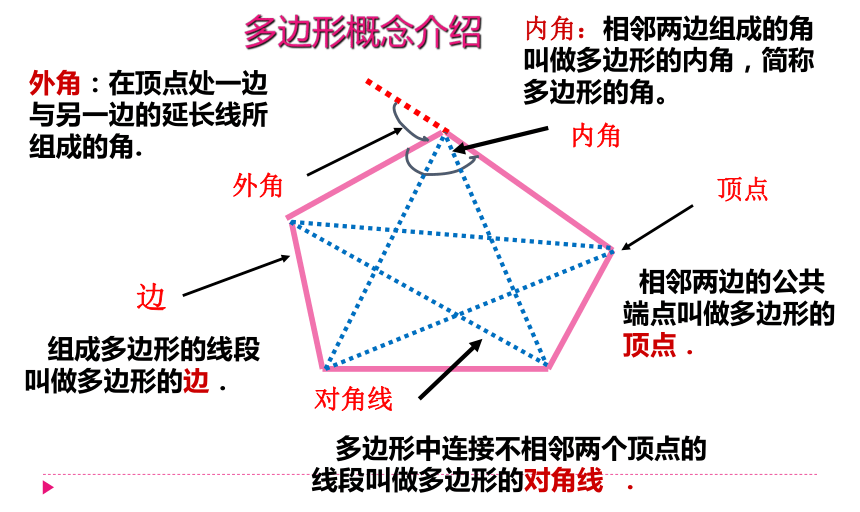
组成多边形的线段叫做多边形的边.
边
顶点
相邻两边的公共端点叫做多边形的顶点.
内角
内角:相邻两边组成的角叫做多边形的内角,简称多边形的角。
外角
外角:在顶点处一边与另一边的延长线所组成的角.
多边形概念介绍
对角线
多边形中连接不相邻两个顶点的线段叫做多边形的对角线 .
我们知道
边数为3的多边形叫三角形,边数为4的多边形叫四边形.
六角螺帽
依此类推,边数为5的多边形叫五边形,……
边数为n的多边形叫n边形.(n为大于或等于3的正整数)
多边形命名
注意:顶点字母按顺时针或逆时针顺序写
多边形命名 : 边形
A
B
C
D
命名 : 边形
四
ABCD
四边形ABCD
A
B
C
D
E
命名 : 边形
五
ABCDE
五边形ABCDE
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形 叫做凸多边形。
图 2
比
一
比
图1
我们所研究的多边形都指凸多边形
新知讲解
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形.
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形.
正三角形
正方形
正五边形
正六边形
(或正三边形)
(或正四边形)
正多边形
新知讲解
讨论1:
n边形有 条对角线
多边形的边数 3 4 5 6 … n
图形
从一个顶点出发对角线数
对角线总数
0
0
3
5
2
1
2
n-3
9
新知探究
D
A
B
C
讨论2:任意四边形的内角和是多少?
2×180 °
新知探究
连接BD
四边形ABCD分成 个三角形
2
四边形ABCD内角和=
△ABD内角和+△DCB的内角和
四边形的内角和是
四边形内角和问题转化为三角形内角和计算
E
A
B
C
D
用类似方法,你能求出五边形的内角和是多少吗?
五边形的内角和是
3×180°
讨论2:
F
A
B
C
D
E
六边形的内角和是多少?
六边形的内角和是 ________
4×180°
多边形的边数 4 5 6 … n
分成三角形的个数 …
多边形的内角和 …
2
3
4
n-2
360°
540°
720°
(n-2)×180°
从多边形的一个顶点出发,引出所有的对角线,从而把多边形分割为多个三角形.
归纳总结
多边形内角和定理:
n边形的内角和等于(n-2) ·1800
﹙n为不小于3的整数﹚
新知讲解
你还有其他的方法计算多边形的内角和吗?
探索多边形的内角和关键是:
把多边形分成几个三角形,再利用三角形的内角和求得。
议
一
议
你还有其它的分法吗?
P
A
E
D
C
B
A
E
D
C
B
P
5×180o-360o
4×180o-180o
例1.已知四边形的四个内角的度数的比为1:2:3:4,求这个四边形最大的角的度数.
例题讲解
解:设每份为x°,由题意得:
x+2x+3x+4x =(4-2)×180
x=36
答:这个四边形最大的角为1440
4×36 =144(度)
最大的角的度数为:
按比例 设出未知数
例2、一个多边形的内角和为1080°,这个多边形是几边形?
解:设这个多边形为n边形,由题意可得:
180°×(n-2)=1080°
解得 : n=8
答:这个多边形为8边形.
例题讲解
利用公式形成方程求解
1、一个正多边形的每个内角等于135°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
课堂练习
D
2、如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2= 度
240°
A
B
D
C
2
1
课堂练习
A
B
D
C
3、如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格 为什么
┓
┏
E
F
G
解:延长AB,CD相交G,由题意得:
五边形AEFCG的内角和=(5-2)×180°=540°
∴∠A+∠E+∠F+∠C+∠AGC=540°
∴∠AGC=540°-122°-90°-90°-155°=83°
∴产品不合格
1、一个凸多边形,除了一个内角外,其余各内角的和为 2750°,求这个多边形的边数以及除去的一个内角的度数.
提升练习
解:设边数为n(n≥3,n为正整数),一个内角x°(0多边形内角和=2750°+x°=(n-2) 180°
∴2750°< (n-2) 180°< 2750°+180°
∴15< n-2< 16
∵n为正整数
∴n=18
x°=(18-2) 180°-2750°=130°
答:这个多边形的边数为18,除去的一个内角为130°.
拓展练习
将一个四边形纸片剪去一个角,剩下的是一个几边形?它的内角和是多少?剪一剪
①
②
③
A
B
C
D
E
M
N
①:剩下是一个三角形,内角和是180°
②剩下是一个四角形,内角和是360°
③剩下是一个五角形,内角和是540°
沪科版数学八年级下册
第19章 四边形
19.1 多边形的内角和
第1课时 多边形及其内角和公式
教学目标
观察下列图形,由这图形你能抽象出什么几何图形?
新知导入
三角形
四边形
五边形
六边形
八边形
四边形
新知讲解
由平面内不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫做三 角 形
三角形的定义:
还记得三角形定义吗?
A
B
C
若将三条线段改为四条、五条。。。。
多边形的定义:
由平面内不在同一直线上的若干条线段首尾顺次连接所组成的封闭图形叫做多边 形
注意:1、所有的线段要在一个平面内
2、线段首尾相连成封闭图形
组成多边形的线段叫做多边形的边.
边
顶点
相邻两边的公共端点叫做多边形的顶点.
内角
内角:相邻两边组成的角叫做多边形的内角,简称多边形的角。
外角
外角:在顶点处一边与另一边的延长线所组成的角.
多边形概念介绍
对角线
多边形中连接不相邻两个顶点的线段叫做多边形的对角线 .
我们知道
边数为3的多边形叫三角形,边数为4的多边形叫四边形.
六角螺帽
依此类推,边数为5的多边形叫五边形,……
边数为n的多边形叫n边形.(n为大于或等于3的正整数)
多边形命名
注意:顶点字母按顺时针或逆时针顺序写
多边形命名 : 边形
A
B
C
D
命名 : 边形
四
ABCD
四边形ABCD
A
B
C
D
E
命名 : 边形
五
ABCDE
五边形ABCDE
一个多边形,如果把它任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形 叫做凸多边形。
图 2
比
一
比
图1
我们所研究的多边形都指凸多边形
新知讲解
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形.
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形.
正三角形
正方形
正五边形
正六边形
(或正三边形)
(或正四边形)
正多边形
新知讲解
讨论1:
n边形有 条对角线
多边形的边数 3 4 5 6 … n
图形
从一个顶点出发对角线数
对角线总数
0
0
3
5
2
1
2
n-3
9
新知探究
D
A
B
C
讨论2:任意四边形的内角和是多少?
2×180 °
新知探究
连接BD
四边形ABCD分成 个三角形
2
四边形ABCD内角和=
△ABD内角和+△DCB的内角和
四边形的内角和是
四边形内角和问题转化为三角形内角和计算
E
A
B
C
D
用类似方法,你能求出五边形的内角和是多少吗?
五边形的内角和是
3×180°
讨论2:
F
A
B
C
D
E
六边形的内角和是多少?
六边形的内角和是 ________
4×180°
多边形的边数 4 5 6 … n
分成三角形的个数 …
多边形的内角和 …
2
3
4
n-2
360°
540°
720°
(n-2)×180°
从多边形的一个顶点出发,引出所有的对角线,从而把多边形分割为多个三角形.
归纳总结
多边形内角和定理:
n边形的内角和等于(n-2) ·1800
﹙n为不小于3的整数﹚
新知讲解
你还有其他的方法计算多边形的内角和吗?
探索多边形的内角和关键是:
把多边形分成几个三角形,再利用三角形的内角和求得。
议
一
议
你还有其它的分法吗?
P
A
E
D
C
B
A
E
D
C
B
P
5×180o-360o
4×180o-180o
例1.已知四边形的四个内角的度数的比为1:2:3:4,求这个四边形最大的角的度数.
例题讲解
解:设每份为x°,由题意得:
x+2x+3x+4x =(4-2)×180
x=36
答:这个四边形最大的角为1440
4×36 =144(度)
最大的角的度数为:
按比例 设出未知数
例2、一个多边形的内角和为1080°,这个多边形是几边形?
解:设这个多边形为n边形,由题意可得:
180°×(n-2)=1080°
解得 : n=8
答:这个多边形为8边形.
例题讲解
利用公式形成方程求解
1、一个正多边形的每个内角等于135°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.八边形
课堂练习
D
2、如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2= 度
240°
A
B
D
C
2
1
课堂练习
A
B
D
C
3、如图所示的模板,按规定,AB,CD的延长线相交成80°的角,因交点不在板上,不便测量,质检员测得∠BAE=122°,∠DCF=155°.如果你是质检员,如何知道模板是否合格 为什么
┓
┏
E
F
G
解:延长AB,CD相交G,由题意得:
五边形AEFCG的内角和=(5-2)×180°=540°
∴∠A+∠E+∠F+∠C+∠AGC=540°
∴∠AGC=540°-122°-90°-90°-155°=83°
∴产品不合格
1、一个凸多边形,除了一个内角外,其余各内角的和为 2750°,求这个多边形的边数以及除去的一个内角的度数.
提升练习
解:设边数为n(n≥3,n为正整数),一个内角x°(0
∴2750°< (n-2) 180°< 2750°+180°
∴15< n-2< 16
∵n为正整数
∴n=18
x°=(18-2) 180°-2750°=130°
答:这个多边形的边数为18,除去的一个内角为130°.
拓展练习
将一个四边形纸片剪去一个角,剩下的是一个几边形?它的内角和是多少?剪一剪
①
②
③
A
B
C
D
E
M
N
①:剩下是一个三角形,内角和是180°
②剩下是一个四角形,内角和是360°
③剩下是一个五角形,内角和是540°
