平面与平面垂直的判定
图片预览





文档简介
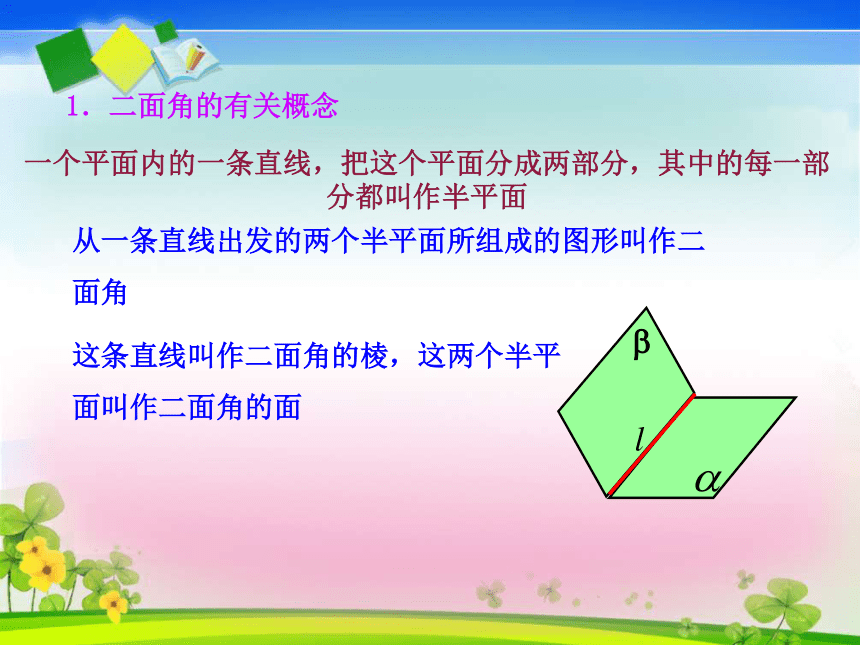
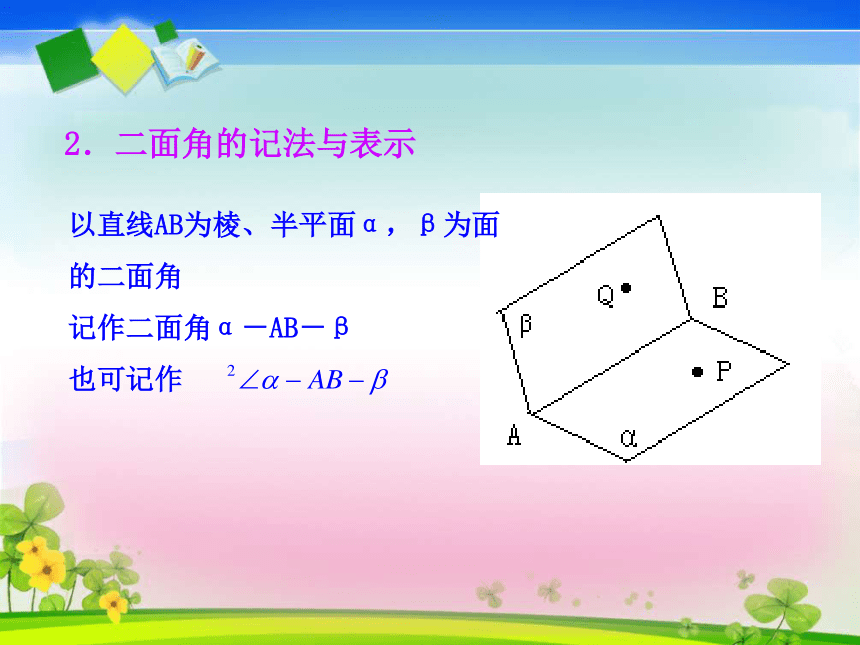
课件24张PPT。第2课时 平面与平面垂直的判定问题1:平面几何中“角”是怎样定义的?问题2:两个平面相交所形成的位置关系不同,你能定量地描述吗?观察开关门-----角?这样的角有何特点,该如何表示呢? 展示一张纸面,并对折观察其形状,将它与角进行类比.1.二面角的有关概念从一条直线出发的两个半平面所组成的图形叫作二面角这条直线叫作二面角的棱,这两个半平面叫作二面角的面?一个平面内的一条直线,把这个平面分成两部分,其中的每一部分都叫作半平面2.二面角的记法与表示以直线AB为棱、半平面α,β为面的二面角
记作二面角α-AB-β
也可记作 二面角的大小反映了两个平面相交的位置关系,
如我们常说“把门开大一些”,是指二面角大一些,
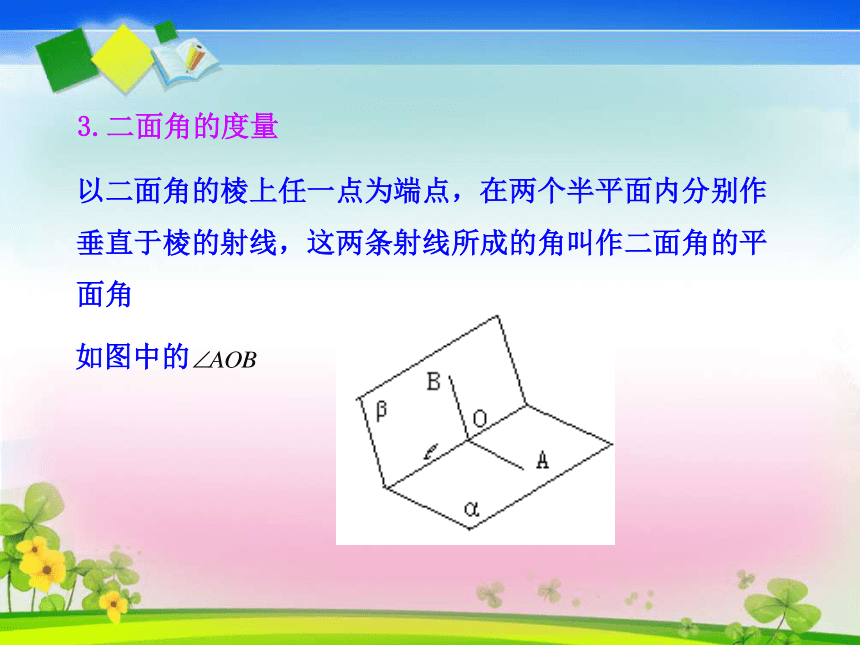
那我们应如何度量二面角的大小呢?3.二面角的度量以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的射线,这两条射线所成的角叫作二面角的平面角如图中的 注意:
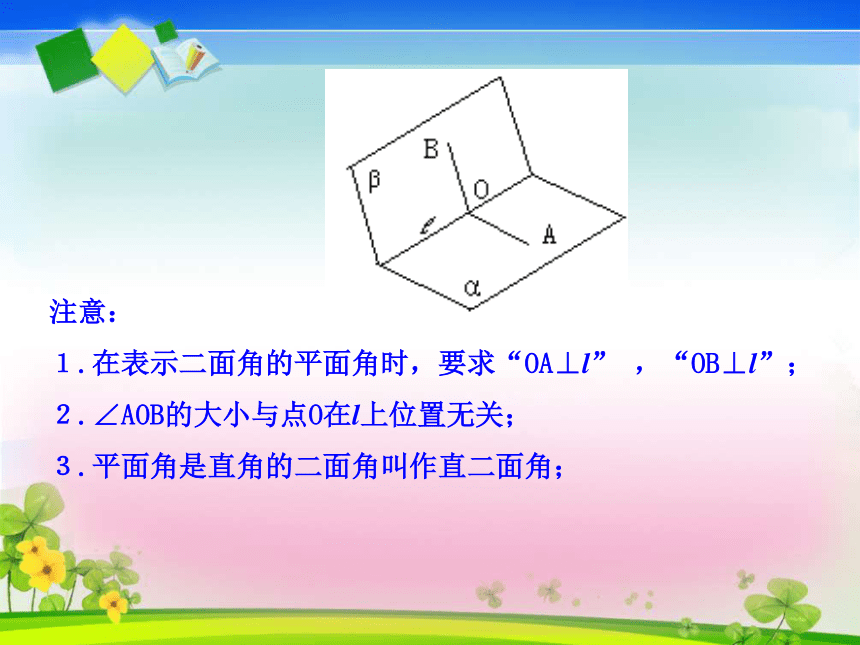
1.在表示二面角的平面角时,要求“OA⊥l”?,“OB⊥l”;
2.∠AOB的大小与点O在l上位置无关;
3.平面角是直角的二面角叫作直二面角; 教室里的墙面所在平面与地面所在平面相交,它们所成的二面角及其度数是多少?思考交流1.两个平面互相垂直的定义
两个平面相交,如果它们所成的二面角是直二面角,
就说这两个平面互相垂直两个平面互相垂直通常画成:
直立平面的竖边画成与水平平面的横边垂直.
平面α与β垂直,记作:α⊥β2.两个平面互相垂直的画法及其表示:问题1:根据定义判断两个平面是否垂直需要解决什么问题?问题2:如图,∠AOB为直二面角α -l-β的平面角,
那么直线AO与平面α的位置关系如何?两个平面垂直的判定定理: 如果一个平面经过另一个平面的一条垂线,那么这两个
平面互相垂直.注:这个定理简称
“线面垂直,则面面垂直”分析:作出它的一个平面角,并证明这个平面角是直角.
如何作平面角呢?
可以作BE⊥CD,使∠ABE为二面角α-CD-β的平面角.求证:证明:设a∩β=CD,则B∈CD.∴AB⊥CD在平面β内过点B作直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角,又AB⊥BE,即二面角α-CD-β是直二面角.∴α⊥β. 两个平面垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出垂直于一个平面的另一个平面的依据.特别提醒:如:建筑工人砌墙例1:如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,
C是圆周一不同于A,B的任意一点,
求证:平面PAC⊥平面PBC证明:设⊙O所在平面为α,
由已知条件,有PA⊥α,BC在α内,
所以,PA⊥BC.
因为,点C是不同于A,B的任意
一点,AB为⊙O的直径,
所以,∠BCA=90°,即BC⊥CA
又因为PA与AC是△PAC所在平面内的两条相交直线,
所以,BC⊥平面PAC,
又因为BC在平面PBC内,
所以,平面PAC⊥平面PBC.思考:你还能发现哪些面互相垂直?1.二面角指的是( )
A.从一条直线出发的两个半平面所夹的角度
B.从一条直线出发的两个半平面所组成的图形
C.两个平面相交时,两个平面所夹的锐角
D.过棱上一点和棱垂直的二射线所成的角B2.判断正误(1)如果平面α内有一条直线垂直于平面β内的一条直线,
则α⊥β.( )(2)如果平面α内有一条直线垂直于平面β内的两条直线,
则α⊥β.( )(3) 如果平面α内的一条直线垂直于平面β内的两条相交直线, 则α⊥β.( )××√1. 角与二面角之间的关系2.二面角的度量
3.两个平面垂直的判定定理的内容
它与直线与平面垂直的判定定理的关系不能把希望叫做白日做梦,也不能把白日之梦叫做希望。
记作二面角α-AB-β
也可记作 二面角的大小反映了两个平面相交的位置关系,
如我们常说“把门开大一些”,是指二面角大一些,
那我们应如何度量二面角的大小呢?3.二面角的度量以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的射线,这两条射线所成的角叫作二面角的平面角如图中的 注意:
1.在表示二面角的平面角时,要求“OA⊥l”?,“OB⊥l”;
2.∠AOB的大小与点O在l上位置无关;
3.平面角是直角的二面角叫作直二面角; 教室里的墙面所在平面与地面所在平面相交,它们所成的二面角及其度数是多少?思考交流1.两个平面互相垂直的定义
两个平面相交,如果它们所成的二面角是直二面角,
就说这两个平面互相垂直两个平面互相垂直通常画成:
直立平面的竖边画成与水平平面的横边垂直.
平面α与β垂直,记作:α⊥β2.两个平面互相垂直的画法及其表示:问题1:根据定义判断两个平面是否垂直需要解决什么问题?问题2:如图,∠AOB为直二面角α -l-β的平面角,
那么直线AO与平面α的位置关系如何?两个平面垂直的判定定理: 如果一个平面经过另一个平面的一条垂线,那么这两个
平面互相垂直.注:这个定理简称
“线面垂直,则面面垂直”分析:作出它的一个平面角,并证明这个平面角是直角.
如何作平面角呢?
可以作BE⊥CD,使∠ABE为二面角α-CD-β的平面角.求证:证明:设a∩β=CD,则B∈CD.∴AB⊥CD在平面β内过点B作直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角,又AB⊥BE,即二面角α-CD-β是直二面角.∴α⊥β. 两个平面垂直的判定定理不仅是判定两个平面互相垂直的依据,而且是找出垂直于一个平面的另一个平面的依据.特别提醒:如:建筑工人砌墙例1:如图,AB为⊙O的直径,PA垂直于⊙O所在的平面,
C是圆周一不同于A,B的任意一点,
求证:平面PAC⊥平面PBC证明:设⊙O所在平面为α,
由已知条件,有PA⊥α,BC在α内,
所以,PA⊥BC.
因为,点C是不同于A,B的任意
一点,AB为⊙O的直径,
所以,∠BCA=90°,即BC⊥CA
又因为PA与AC是△PAC所在平面内的两条相交直线,
所以,BC⊥平面PAC,
又因为BC在平面PBC内,
所以,平面PAC⊥平面PBC.思考:你还能发现哪些面互相垂直?1.二面角指的是( )
A.从一条直线出发的两个半平面所夹的角度
B.从一条直线出发的两个半平面所组成的图形
C.两个平面相交时,两个平面所夹的锐角
D.过棱上一点和棱垂直的二射线所成的角B2.判断正误(1)如果平面α内有一条直线垂直于平面β内的一条直线,
则α⊥β.( )(2)如果平面α内有一条直线垂直于平面β内的两条直线,
则α⊥β.( )(3) 如果平面α内的一条直线垂直于平面β内的两条相交直线, 则α⊥β.( )××√1. 角与二面角之间的关系2.二面角的度量
3.两个平面垂直的判定定理的内容
它与直线与平面垂直的判定定理的关系不能把希望叫做白日做梦,也不能把白日之梦叫做希望。
