8.2重力势能课件(47张PPT)
文档属性
| 名称 | 8.2重力势能课件(47张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-10 18:21:22 | ||
图片预览










文档简介
(共47张PPT)
第八章 机械能守恒定律
第1节 功与功率
教学目标
①知道重力做功的特点,与路径无关;
②理解重力势能及重力做功与重力势能变化的关系;
③知道重力势能具有相对性,知道重力势能是物体和地球组成的“系统”所共有的;
④理解弹性势能,知道影响弹性势能大小的相关因素;
教学重点
①知道重力做功的特点,与路径无关;
②理解重力势能及重力做功与重力势能变化的关系;
③知道重力势能具有相对性;
④理解弹性势能,知道影响弹性势能大小的相关因素;
教学难点
①知道重力做功的特点,与路径无关,理解重力势能及重力做功与重力势能变化的关系;
②知道重力势能具有相对性;
复习回顾
1、功的概念和表达式
2、功是标量,但有正负。正负代表什么含义呢?
3、如何求总功?
总功等于各个力对物体所做功的代数和,也等于合力对物体所做的功。
4、功率的定义与表达式。
新课讲授
问题与探究
初中我们已经定性的学习了重力势能,物体的质量越大、所处的位置越高,重力势能就越大。本节课我们来进一步定性的研究一下重力势能,学习一下重力势能的表达式。
我们知道,当物体的高度变化时,重力做功,势能发生变化:物体下降时,重力做正功,势能减小;物体上升时,重力做负功,势能增。可见重力做功和重力势能是密切相关的,我们先来研究一下重力做功。
一、重力做功
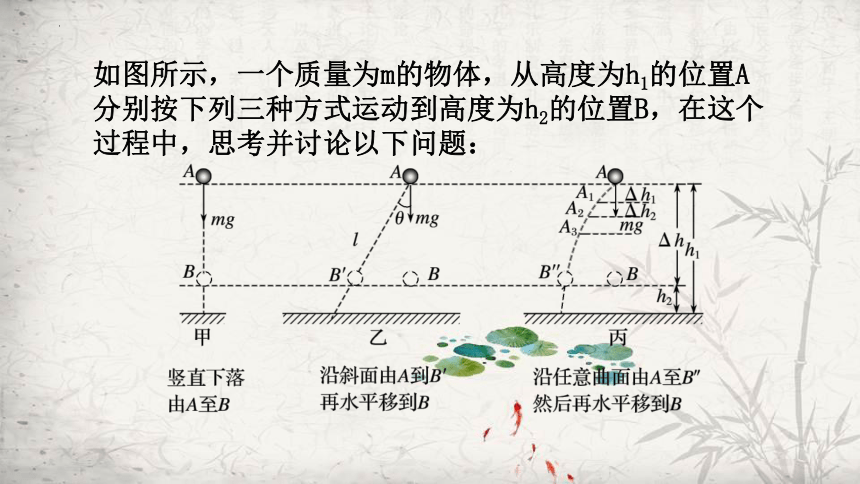
如图所示,一个质量为m的物体,从高度为h1的位置A分别按下列三种方式运动到高度为h2的位置B,在这个过程中,思考并讨论以下问题:
(1)竖直下落时
重力做功:
WG=mg·Δh
=mgh1-mgh2
(2)沿着斜面时
重力做功:
WG=mg·l·cosθ
=mg·Δh
=mgh1-mgh2
(3)沿着曲面时
图丙中把整个路径AB″分成许多很短的间隔AA1、A1A2…,由于每一段都很小,每一小段都可以近似地看成一段倾斜的直线,则物体通过每段小斜线时重力做的功分别为mgΔh1、mgΔh2….
WG=mgΔh1+mgΔh2+…=mg(Δh1+Δh2+…)=mgΔh
故WG=mgΔh=mgh1-mgh2.
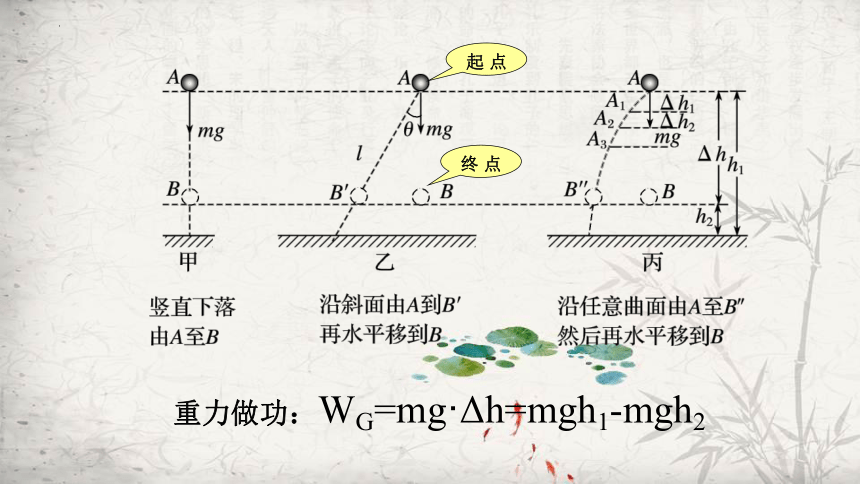
重力做功:
WG=mg·Δh=mgh1-mgh2
起 点
终 点
我们发现:上述三种情况中,尽管物体的运动路径不同,但是高度的变化是一样的,而且重力做功也是一样的。
物体运动时,重力对它做的功只跟它的起点和终点的位置有关(高度差),而跟物体运动的路径无关。
重力做功的特点可推广到任一恒力做功,即恒力做功的特点是:与具体路径无关,即恒力做的功等于力与在力的方向上的位移大小的乘积,跟初、末位置有关
推广:
重力做功的特点:
1.某游客领着孩子游泰山时,孩子不小心将手中质量为m的皮球滑落,球从A点滚到了山脚下的B点,高度标记如图3所示,重力加速度为g,则下列说法正确的是
A.从A到B的曲线轨迹长度不知道,无法求出
此过程重力做的功
B.从A到B过程中阻力大小不知道,无法求出
此过程重力做的功
C.从A到B重力做功mg(H+h)
D.从A到B重力做功mgH
D
2、如图1所示,质量关系为m1>m2>m3的三个小球分别沿三条不同的轨道1、2、3由离地高h的A点滑到同一水平面上,轨道1、3是光滑的,轨道2是粗糙的,重力对小球做的功分别为W1、W2、
W3,则下列判断正确的是
A.W1>W2=W3 B.W1=W3>W2
C.W1=W2=W3 D.W1>W2>W3
C
3、如图2所示,质量为m的小球从高为h处的斜面上的A点滚下,经过水平面BC后,再滚上另一斜面,当它到达 处的D点时,速度为零,在这个过程中,重力做功为(重力加速度为g)
B
4、如图6所示,长为2 m、质量为10 kg的一条细铁链放在水平地面上,从提起铁链一端直到铁链全部离开地面的瞬间,铁链克服重力做的功为多少?(g取9.8 m/s2)
B
思考:重力做功与物体受到的其他力有关吗?与物体做加速运动还是减速运动有关吗?
都无关,重力做功只与重力和物体的高度变化有关
二、重力势能
由重力做功的表达式WG=mgΔh=mgh1-mgh2可以看出重力做功与初末位置的mgh有关。而mgh与我们学习过的重力势能特征一致。因此我们把mgh叫做物体的重力势能,常用EP表示。
EP=mgh
重力势能和其他能一样,都是标量,单位都是焦耳,符号为J。
重力做功与重力势能的关系
其中:EP1=mgh1表示初位置的重力势能;
EP2=mgh2表示末位置的重力势能;
-ΔEP表示重力势能的变化量。
总结:①重力做了多少功就有多少重力势能发生改变。
②重力对物体做正功的大小等于重力势能的减少量
③重力对物体做负功的大小等于重力势能的增加量
WG=mg·Δh
=mgh1-mgh2
=EP1-EP2
=-ΔEP
(多选)物体在运动过程中,克服重力做功100 J,则以下说法正确的是
A.物体的高度一定降低了
B.物体的高度一定升高了
C.物体的重力势能一定是100 J
D.物体的重力势能一定增加100 J
BD
三、重力势能的相对性
想一想
小明从五楼的窗台上跳下来为什么会安然无恙?
答:向里跳到五楼的地板上
高度具有相对性,选不同的参考平面,高度也不同。
重力势能的相对性
由于高度h具有相对性,所以重力势能mgh也具有相对性。
注意:
(1)计算重力势能之前需要先选定参考平面(又叫零势能面)
(2)在参考面上方的物体的高度是正值,重力势能也是正值;在参考面下方的物体的高度是负值,重力势能也是负值
(3)参考面的选取是任意的,一般选择地面为参考面。
思考:
重力势能是标量,只有大小而没有方向。但是有正负之分,这里的正负号代表什么含义呢?
这里正负代表大小。比如 1>-2。
如图所示,水平桌面距地面的高度为0.8 m,一物体(可看成质点)质量为2 kg,放在桌面上方0.4 m的支架上,则:(g取10 m/s2)
h1
h2
A
B
参考面 小球在A处的重力势能 小球在B处的重力势能 整个过程中重力做功 整个过程中重力势能的变化
桌 面
地 面
16J
- 8J
24J
减少24J
24J
0
24J
减少24J
总结:重力势能是相对的,它的大小与参考平面的选取有关,而重力势能的变化量是绝对的,它与参考平面的选取无关.
思考:
重力势能Ep=mgh中的“h”与重力做功W=mgΔh中的“Δh”相同吗?若不同,有何区别?
不相同.重力势能Ep=mgh中的“h”是物体相对于参考平面的高度;而重力做功W=mgΔh中的“Δh”是物体初、末位置的高度差,与参考平面无关.
重力势能的系统性
重力势能是地球与物体所组成的物体“系统”所共有的,而不是地球上的物体单独具有的。
1、关于重力势能,下列说法中正确的是
A.放在地面上的物体重力势能一定为零
B.物体与参考平面的距离越大,它的重力势能也越大
C.重力势能的变化量与参考平面的选取无关
D.一个物体的重力势能从-10 J变化到4 J,重力势能减少了
C
2、如图3所示,质量为m的足球在水平地面的位置1被踢出后落到水平地面的位置3,在空中达到的最高点位置2的高度为h,已知重力加速度为g.下列说法正确的是
A.足球由1运动到2的过程中,重力做的功为
mgh
B.足球由2运动到3的过程中,重力势能减少了mgh
C.足球由1运动到3的过程中,重力做的功为2mgh
D.因为没有选定参考平面,所以无法确定重力势能变化了多少
B
四、弹性势能
生活中有许多这样的例子,这些物体都发生了弹性形变,物体的各部分之间由于有弹力的相互作用,而具有势能,这种势能就叫作弹性势能。
情景分析:
如图所示,物体与水平轻质弹簧相连,物体在O点时弹簧处于原长,把物体向右拉到A处静止释放,物体会由A向A′运动,A、A′关于O点对称,则:
(1)物体由A向O运动的过程中,弹力做什么功?弹性势能如何变化?
(2)物体由O向A′运动的过程中,弹力做什么功?弹性势能如何变化?
正功
(3)在A、A′处弹性势能有什么关系?
减少
负功
增加
一样大
(4)弹力做功与弹性势能的关系
WF=EP1-EP2=-ΔEP
弹簧的弹性势能大小关系:
通过上述的例子不难发现弹簧的弹性势能大小与伸长量x和弹簧的劲度系数k有关。
弹簧的伸长量x越大,弹性势能越大
弹簧的劲度系数k越大,弹性势能越大
弹簧的弹性势能的公式:
弹性势能的系统性
弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量,因此弹性势能具有系统性.
弹性势能的相对性
弹性势能的大小与选定的弹性势能为零的位置有关,对于弹簧,一般规定弹簧处于原长时的弹性势能为零,此时弹性势能没有负值。
关于弹簧的弹性势能,下列说法正确的是
A.当弹簧变长时,它的弹性势能一定增大
B.当弹簧变短时,它的弹性势能一定变小
C.在拉伸长度相同时,劲度系数越大的弹簧,它的弹性势能越大
D.弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能
C
1、关于重力做功和重力势能,下列说法中正确的是
A.重力做功与路径无关
B.当物体克服重力做功时,物体的重力势能一定减小
C.重力势能为负值,说明其方向与规定的正方向相反
D.重力势能的大小与参考平面的选取无关
课堂练习
A
2、如今高层居民小区越来越多,家住高层,窗外“风光无限”,可电梯房虽好,就是怕停电.要是电梯停运了,给高层住户的生活带来很多不便.家住10楼的李同学某次停电时步行从一楼走楼梯回家,已知该同学质量为50 kg,每层楼的高度为3 m,取g=10 m/s2.则该同学在这个过程中
A.重力做负功,楼梯的支持力做正功
B.重力做负功,楼梯的支持力不做功
C.重力势能增加1.5×105 J
D.重力势能增加1.35×105 J
课堂练习
A
3、(多选)关于弹簧的弹性势能,下列说法正确的是
A.弹簧的弹性势能与其被拉伸(或压缩)的长度有关
B.弹簧的弹性势能与弹簧的劲度系数有关
C.同一弹簧,在弹性限度内,形变量越大,弹性势能越大
D.弹性势能的大小与使弹簧发生形变的物体有关
课堂练习
ABC
4、如图所示,在光滑水平面上有一物体,它的左端与一水平轻质弹簧连接,弹簧的另一端固定在墙上,在力F的作用下物体处于静止状态.当撤去F后,物体将向右运动,在物体向右运动的过程中,下列说法正确的是(弹簧始终在弹性限度内)
A.弹簧的弹性势能先减小后增大
B.弹簧的弹性势能先增大后减小
C.弹簧的弹性势能逐渐减小
D.弹簧的弹性势能逐渐增大
课堂练习
B
课堂练习
5、如图所示,一质量为m、长度为l的均匀柔软细绳PQ竖直悬挂.用外力将绳的下端Q缓慢地竖直向上拉起至M点,M点与绳的上端P相距 .重力加速度大小为g.在此过程中,绳的重力势能增加
A
6、如图甲所示,一滑块沿光滑的水平面向左运动,与水平轻弹簧接触后将弹簧压缩到最短,然后反向弹回,弹簧始终处在弹性限度内,图乙为测得的弹簧的弹力与弹簧压缩量之间的关系图像,则弹簧的压缩量由8 cm变为4 cm时,弹簧所做的功以及弹性势能的变化量分别为
A.3.6 J、-3.6 J
B.-3.6 J、3.6 J
C.1.8 J、-1.8 J
D.-1.8 J、1.8 J
C
7、如图7所示的蹦极运动是一种非常刺激的娱乐项目.为了研究蹦极运动过程,做以下简化:将游客视为质点,他的运动始终沿竖直方向.弹性绳的一端固定在O点,另一端和游客相连.游客从O点自由下落,至B点弹性绳自然伸直,经过合力为零的C点到达最低点D,然后弹起,整个过程中弹性绳始终在弹性限度内.游客从O→B→C→D的过程,下列说法正确的是
A.从O到B过程中,重力势能增大
B.从B到D过程中,游客做匀减速运动
C.从B到C过程中,弹性绳的弹性势能先增大后减小
D.从B到D过程中,游客的速度先增大后减小
D
8、如图所示,吊车以 的加速度将质量为m的物体匀减速地沿竖直方向提升高度h,则:(重力加速度为g,不计空气阻力)
课堂练习
(1)吊车钢索的拉力对物体做的功为多少?
(2)重力做的功为多少?
(3)物体的重力势能变化了多少?
(1)吊车钢索的拉力对物体做的功为多少?
由牛顿第二定律得mg-F=ma,
(2)重力做的功为多少?
解析 物体被提升高度为h,重力做的功WG=-mgh.
(3)物体的重力势能变化了多少?
解析 由于ΔEp=-WG=mgh,故物体的重力势能增加了mgh.
9、如图所示,质量相等的两木块中间连有一竖直弹簧,今用力F缓慢向上提A,直到B恰好离开水平地面.开始时木块A静止在弹簧上面.设开始时弹簧的弹性势能为Ep1,B刚要离开地面时,弹簧的弹性势能为Ep2,则关于Ep1、Ep2的大小关系及弹性势能的变化ΔEp,下列说法中正确的是
A.Ep1=Ep2 B.Ep1>Ep2
C.ΔEp>0 D.ΔEp<0
A
课堂小结
1、重力做功的表达式,重力势能的表达式
2、重力做功和重力势能的关系
3、计算重力势能时应该先确定什么?
4、弹力做功和弹性力势能的关系?
5、弹力弹性力势能的表达式?
练习与作业
完成课后习题
第八章 机械能守恒定律
第1节 功与功率
教学目标
①知道重力做功的特点,与路径无关;
②理解重力势能及重力做功与重力势能变化的关系;
③知道重力势能具有相对性,知道重力势能是物体和地球组成的“系统”所共有的;
④理解弹性势能,知道影响弹性势能大小的相关因素;
教学重点
①知道重力做功的特点,与路径无关;
②理解重力势能及重力做功与重力势能变化的关系;
③知道重力势能具有相对性;
④理解弹性势能,知道影响弹性势能大小的相关因素;
教学难点
①知道重力做功的特点,与路径无关,理解重力势能及重力做功与重力势能变化的关系;
②知道重力势能具有相对性;
复习回顾
1、功的概念和表达式
2、功是标量,但有正负。正负代表什么含义呢?
3、如何求总功?
总功等于各个力对物体所做功的代数和,也等于合力对物体所做的功。
4、功率的定义与表达式。
新课讲授
问题与探究
初中我们已经定性的学习了重力势能,物体的质量越大、所处的位置越高,重力势能就越大。本节课我们来进一步定性的研究一下重力势能,学习一下重力势能的表达式。
我们知道,当物体的高度变化时,重力做功,势能发生变化:物体下降时,重力做正功,势能减小;物体上升时,重力做负功,势能增。可见重力做功和重力势能是密切相关的,我们先来研究一下重力做功。
一、重力做功
如图所示,一个质量为m的物体,从高度为h1的位置A分别按下列三种方式运动到高度为h2的位置B,在这个过程中,思考并讨论以下问题:
(1)竖直下落时
重力做功:
WG=mg·Δh
=mgh1-mgh2
(2)沿着斜面时
重力做功:
WG=mg·l·cosθ
=mg·Δh
=mgh1-mgh2
(3)沿着曲面时
图丙中把整个路径AB″分成许多很短的间隔AA1、A1A2…,由于每一段都很小,每一小段都可以近似地看成一段倾斜的直线,则物体通过每段小斜线时重力做的功分别为mgΔh1、mgΔh2….
WG=mgΔh1+mgΔh2+…=mg(Δh1+Δh2+…)=mgΔh
故WG=mgΔh=mgh1-mgh2.
重力做功:
WG=mg·Δh=mgh1-mgh2
起 点
终 点
我们发现:上述三种情况中,尽管物体的运动路径不同,但是高度的变化是一样的,而且重力做功也是一样的。
物体运动时,重力对它做的功只跟它的起点和终点的位置有关(高度差),而跟物体运动的路径无关。
重力做功的特点可推广到任一恒力做功,即恒力做功的特点是:与具体路径无关,即恒力做的功等于力与在力的方向上的位移大小的乘积,跟初、末位置有关
推广:
重力做功的特点:
1.某游客领着孩子游泰山时,孩子不小心将手中质量为m的皮球滑落,球从A点滚到了山脚下的B点,高度标记如图3所示,重力加速度为g,则下列说法正确的是
A.从A到B的曲线轨迹长度不知道,无法求出
此过程重力做的功
B.从A到B过程中阻力大小不知道,无法求出
此过程重力做的功
C.从A到B重力做功mg(H+h)
D.从A到B重力做功mgH
D
2、如图1所示,质量关系为m1>m2>m3的三个小球分别沿三条不同的轨道1、2、3由离地高h的A点滑到同一水平面上,轨道1、3是光滑的,轨道2是粗糙的,重力对小球做的功分别为W1、W2、
W3,则下列判断正确的是
A.W1>W2=W3 B.W1=W3>W2
C.W1=W2=W3 D.W1>W2>W3
C
3、如图2所示,质量为m的小球从高为h处的斜面上的A点滚下,经过水平面BC后,再滚上另一斜面,当它到达 处的D点时,速度为零,在这个过程中,重力做功为(重力加速度为g)
B
4、如图6所示,长为2 m、质量为10 kg的一条细铁链放在水平地面上,从提起铁链一端直到铁链全部离开地面的瞬间,铁链克服重力做的功为多少?(g取9.8 m/s2)
B
思考:重力做功与物体受到的其他力有关吗?与物体做加速运动还是减速运动有关吗?
都无关,重力做功只与重力和物体的高度变化有关
二、重力势能
由重力做功的表达式WG=mgΔh=mgh1-mgh2可以看出重力做功与初末位置的mgh有关。而mgh与我们学习过的重力势能特征一致。因此我们把mgh叫做物体的重力势能,常用EP表示。
EP=mgh
重力势能和其他能一样,都是标量,单位都是焦耳,符号为J。
重力做功与重力势能的关系
其中:EP1=mgh1表示初位置的重力势能;
EP2=mgh2表示末位置的重力势能;
-ΔEP表示重力势能的变化量。
总结:①重力做了多少功就有多少重力势能发生改变。
②重力对物体做正功的大小等于重力势能的减少量
③重力对物体做负功的大小等于重力势能的增加量
WG=mg·Δh
=mgh1-mgh2
=EP1-EP2
=-ΔEP
(多选)物体在运动过程中,克服重力做功100 J,则以下说法正确的是
A.物体的高度一定降低了
B.物体的高度一定升高了
C.物体的重力势能一定是100 J
D.物体的重力势能一定增加100 J
BD
三、重力势能的相对性
想一想
小明从五楼的窗台上跳下来为什么会安然无恙?
答:向里跳到五楼的地板上
高度具有相对性,选不同的参考平面,高度也不同。
重力势能的相对性
由于高度h具有相对性,所以重力势能mgh也具有相对性。
注意:
(1)计算重力势能之前需要先选定参考平面(又叫零势能面)
(2)在参考面上方的物体的高度是正值,重力势能也是正值;在参考面下方的物体的高度是负值,重力势能也是负值
(3)参考面的选取是任意的,一般选择地面为参考面。
思考:
重力势能是标量,只有大小而没有方向。但是有正负之分,这里的正负号代表什么含义呢?
这里正负代表大小。比如 1>-2。
如图所示,水平桌面距地面的高度为0.8 m,一物体(可看成质点)质量为2 kg,放在桌面上方0.4 m的支架上,则:(g取10 m/s2)
h1
h2
A
B
参考面 小球在A处的重力势能 小球在B处的重力势能 整个过程中重力做功 整个过程中重力势能的变化
桌 面
地 面
16J
- 8J
24J
减少24J
24J
0
24J
减少24J
总结:重力势能是相对的,它的大小与参考平面的选取有关,而重力势能的变化量是绝对的,它与参考平面的选取无关.
思考:
重力势能Ep=mgh中的“h”与重力做功W=mgΔh中的“Δh”相同吗?若不同,有何区别?
不相同.重力势能Ep=mgh中的“h”是物体相对于参考平面的高度;而重力做功W=mgΔh中的“Δh”是物体初、末位置的高度差,与参考平面无关.
重力势能的系统性
重力势能是地球与物体所组成的物体“系统”所共有的,而不是地球上的物体单独具有的。
1、关于重力势能,下列说法中正确的是
A.放在地面上的物体重力势能一定为零
B.物体与参考平面的距离越大,它的重力势能也越大
C.重力势能的变化量与参考平面的选取无关
D.一个物体的重力势能从-10 J变化到4 J,重力势能减少了
C
2、如图3所示,质量为m的足球在水平地面的位置1被踢出后落到水平地面的位置3,在空中达到的最高点位置2的高度为h,已知重力加速度为g.下列说法正确的是
A.足球由1运动到2的过程中,重力做的功为
mgh
B.足球由2运动到3的过程中,重力势能减少了mgh
C.足球由1运动到3的过程中,重力做的功为2mgh
D.因为没有选定参考平面,所以无法确定重力势能变化了多少
B
四、弹性势能
生活中有许多这样的例子,这些物体都发生了弹性形变,物体的各部分之间由于有弹力的相互作用,而具有势能,这种势能就叫作弹性势能。
情景分析:
如图所示,物体与水平轻质弹簧相连,物体在O点时弹簧处于原长,把物体向右拉到A处静止释放,物体会由A向A′运动,A、A′关于O点对称,则:
(1)物体由A向O运动的过程中,弹力做什么功?弹性势能如何变化?
(2)物体由O向A′运动的过程中,弹力做什么功?弹性势能如何变化?
正功
(3)在A、A′处弹性势能有什么关系?
减少
负功
增加
一样大
(4)弹力做功与弹性势能的关系
WF=EP1-EP2=-ΔEP
弹簧的弹性势能大小关系:
通过上述的例子不难发现弹簧的弹性势能大小与伸长量x和弹簧的劲度系数k有关。
弹簧的伸长量x越大,弹性势能越大
弹簧的劲度系数k越大,弹性势能越大
弹簧的弹性势能的公式:
弹性势能的系统性
弹性势能是发生弹性形变的物体上所有质点因相对位置改变而具有的能量,因此弹性势能具有系统性.
弹性势能的相对性
弹性势能的大小与选定的弹性势能为零的位置有关,对于弹簧,一般规定弹簧处于原长时的弹性势能为零,此时弹性势能没有负值。
关于弹簧的弹性势能,下列说法正确的是
A.当弹簧变长时,它的弹性势能一定增大
B.当弹簧变短时,它的弹性势能一定变小
C.在拉伸长度相同时,劲度系数越大的弹簧,它的弹性势能越大
D.弹簧在拉伸时的弹性势能一定大于压缩时的弹性势能
C
1、关于重力做功和重力势能,下列说法中正确的是
A.重力做功与路径无关
B.当物体克服重力做功时,物体的重力势能一定减小
C.重力势能为负值,说明其方向与规定的正方向相反
D.重力势能的大小与参考平面的选取无关
课堂练习
A
2、如今高层居民小区越来越多,家住高层,窗外“风光无限”,可电梯房虽好,就是怕停电.要是电梯停运了,给高层住户的生活带来很多不便.家住10楼的李同学某次停电时步行从一楼走楼梯回家,已知该同学质量为50 kg,每层楼的高度为3 m,取g=10 m/s2.则该同学在这个过程中
A.重力做负功,楼梯的支持力做正功
B.重力做负功,楼梯的支持力不做功
C.重力势能增加1.5×105 J
D.重力势能增加1.35×105 J
课堂练习
A
3、(多选)关于弹簧的弹性势能,下列说法正确的是
A.弹簧的弹性势能与其被拉伸(或压缩)的长度有关
B.弹簧的弹性势能与弹簧的劲度系数有关
C.同一弹簧,在弹性限度内,形变量越大,弹性势能越大
D.弹性势能的大小与使弹簧发生形变的物体有关
课堂练习
ABC
4、如图所示,在光滑水平面上有一物体,它的左端与一水平轻质弹簧连接,弹簧的另一端固定在墙上,在力F的作用下物体处于静止状态.当撤去F后,物体将向右运动,在物体向右运动的过程中,下列说法正确的是(弹簧始终在弹性限度内)
A.弹簧的弹性势能先减小后增大
B.弹簧的弹性势能先增大后减小
C.弹簧的弹性势能逐渐减小
D.弹簧的弹性势能逐渐增大
课堂练习
B
课堂练习
5、如图所示,一质量为m、长度为l的均匀柔软细绳PQ竖直悬挂.用外力将绳的下端Q缓慢地竖直向上拉起至M点,M点与绳的上端P相距 .重力加速度大小为g.在此过程中,绳的重力势能增加
A
6、如图甲所示,一滑块沿光滑的水平面向左运动,与水平轻弹簧接触后将弹簧压缩到最短,然后反向弹回,弹簧始终处在弹性限度内,图乙为测得的弹簧的弹力与弹簧压缩量之间的关系图像,则弹簧的压缩量由8 cm变为4 cm时,弹簧所做的功以及弹性势能的变化量分别为
A.3.6 J、-3.6 J
B.-3.6 J、3.6 J
C.1.8 J、-1.8 J
D.-1.8 J、1.8 J
C
7、如图7所示的蹦极运动是一种非常刺激的娱乐项目.为了研究蹦极运动过程,做以下简化:将游客视为质点,他的运动始终沿竖直方向.弹性绳的一端固定在O点,另一端和游客相连.游客从O点自由下落,至B点弹性绳自然伸直,经过合力为零的C点到达最低点D,然后弹起,整个过程中弹性绳始终在弹性限度内.游客从O→B→C→D的过程,下列说法正确的是
A.从O到B过程中,重力势能增大
B.从B到D过程中,游客做匀减速运动
C.从B到C过程中,弹性绳的弹性势能先增大后减小
D.从B到D过程中,游客的速度先增大后减小
D
8、如图所示,吊车以 的加速度将质量为m的物体匀减速地沿竖直方向提升高度h,则:(重力加速度为g,不计空气阻力)
课堂练习
(1)吊车钢索的拉力对物体做的功为多少?
(2)重力做的功为多少?
(3)物体的重力势能变化了多少?
(1)吊车钢索的拉力对物体做的功为多少?
由牛顿第二定律得mg-F=ma,
(2)重力做的功为多少?
解析 物体被提升高度为h,重力做的功WG=-mgh.
(3)物体的重力势能变化了多少?
解析 由于ΔEp=-WG=mgh,故物体的重力势能增加了mgh.
9、如图所示,质量相等的两木块中间连有一竖直弹簧,今用力F缓慢向上提A,直到B恰好离开水平地面.开始时木块A静止在弹簧上面.设开始时弹簧的弹性势能为Ep1,B刚要离开地面时,弹簧的弹性势能为Ep2,则关于Ep1、Ep2的大小关系及弹性势能的变化ΔEp,下列说法中正确的是
A.Ep1=Ep2 B.Ep1>Ep2
C.ΔEp>0 D.ΔEp<0
A
课堂小结
1、重力做功的表达式,重力势能的表达式
2、重力做功和重力势能的关系
3、计算重力势能时应该先确定什么?
4、弹力做功和弹性力势能的关系?
5、弹力弹性力势能的表达式?
练习与作业
完成课后习题
