解一元一次方程课件
图片预览






文档简介
课件18张PPT。 求解一元一次方程——移项运用等式的基本性质解下列方程(1) x + 2 = 1 x + 2 -2 = 1-2. x =-1.解:两边都减去2,得等式的性质1合并同类项,得即:等式两边都加上或减去同一个数或同一个整式,所得结果仍是等式.(2) 3x = -6 即:x =-2.解:两边都除以3,得等式的性质2即:等式两边都乘或除以同一个不等于0的数,所得结果仍是等式. (1)4x - 15 = 9解:两边都减去 5x ,得-3x=-21.系数化为1,得x = 6. (2) 2x = 5x -21解:两边都加上 15 ,得系数化为1,得x = 7.合并同类项 ,得合并同类项 ,得4x = 24.2x = 5x –214x – 15 = 9 4x= 9+15. 2x -5x = -21.你能发现什么吗? 解方程:设问导读阅读教材P135~P136,完成下列问题
1(1)把方程中的一项___后,从方程的______叫移项。
(2)解方程2x+6=1,第一步将+6从方程的左边移到方程的右边相当于方程的两边同时_____,因而移项的依据是等式的基本性质______,具体内容是_______。
(3)移项的目的是:把含有未知数的项移到方程的一遍,常数项移到方程的另一边。
(4)移项时,移动的项要_____,不移动的项_______
2、阅读例题,明确一元一次方程的一般步骤:
______、______、______ _ 这个变形相当于把 ①中的 “– 15”这一项由方程 ①到方程 ② , “– 15”这项移动后,发生了什么变化?
改变了符号 从方程的左边移到
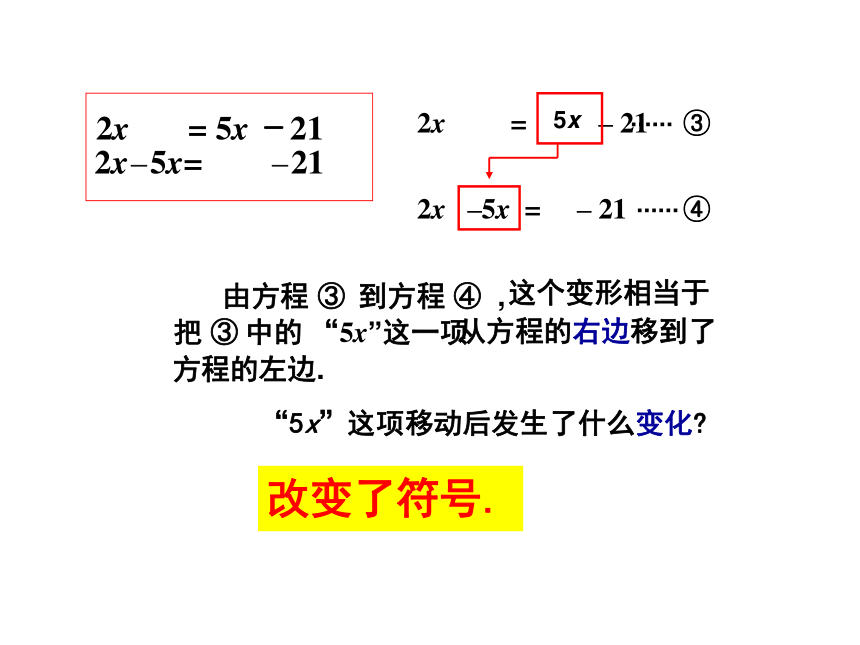
了方程的右边.-15 这个变形相当于把 ③ 中的 “5x”这一项由方程 ③到方程 ④ , “5x”这项移动后发生了什么变化?改变了符号. 从方程的右边移到了方程的左边. 5x 一般地,把方程中的某些项改变符号
后,从方程的一边移到另一边,这种变
形叫做移项. 定义移项目的 把所有含有未知数的项移到方程的一边,把所有常数项移到方程的一边。一般地,把含有未知数的项移到方程的左边,常数项移到方程的右边注:移项要变号自学检测
练习1:把下列方程进行移项变换练习2:判断下列移项是否正确:3x+7=2-2x,移项,得3x-2x=2-7.
2.化简:2x+8y-6x =2x+6x-8y
=8x-8y.慧眼找错错正确答案:3x+2x=2-7.错正确答案:2x+8y-6x=2x-6x+8y
= -4x+8y.化简多项式交换两项位置时不改变项的符号;
解方程移项时必须改变项的符号.练习3例1 解方程 4x-15=9解: 移项,得4x=9+15.合并同类项,得4x=24.系数化为1,得x=6.练习4 解方程解:两边都加上15,得4x=9+15合并同类项,得4x=24系数化为1,得x=6移项实际上是利用等式的性质1,但是解题步骤更为简捷!例2 解方程解:移项,得合并同类项 ,得例2 解方程 解一元一次方程时,
一般把含未知数的项移
到方程的左边,常数项
移到方程的右边.系数化为1,得练习5 解方程例题3:解:移项,得:合并同类项,得:化系数为1,得:练习6 解下列一元一次方程1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。 3.移项要改变符号.2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).这节课我们学习了什么?移项拓展探究:解下列一元一次方程:谢谢你们认真听课!这是对老师最大的鼓励!
1(1)把方程中的一项___后,从方程的______叫移项。
(2)解方程2x+6=1,第一步将+6从方程的左边移到方程的右边相当于方程的两边同时_____,因而移项的依据是等式的基本性质______,具体内容是_______。
(3)移项的目的是:把含有未知数的项移到方程的一遍,常数项移到方程的另一边。
(4)移项时,移动的项要_____,不移动的项_______
2、阅读例题,明确一元一次方程的一般步骤:
______、______、______ _ 这个变形相当于把 ①中的 “– 15”这一项由方程 ①到方程 ② , “– 15”这项移动后,发生了什么变化?
改变了符号 从方程的左边移到
了方程的右边.-15 这个变形相当于把 ③ 中的 “5x”这一项由方程 ③到方程 ④ , “5x”这项移动后发生了什么变化?改变了符号. 从方程的右边移到了方程的左边. 5x 一般地,把方程中的某些项改变符号
后,从方程的一边移到另一边,这种变
形叫做移项. 定义移项目的 把所有含有未知数的项移到方程的一边,把所有常数项移到方程的一边。一般地,把含有未知数的项移到方程的左边,常数项移到方程的右边注:移项要变号自学检测
练习1:把下列方程进行移项变换练习2:判断下列移项是否正确:3x+7=2-2x,移项,得3x-2x=2-7.
2.化简:2x+8y-6x =2x+6x-8y
=8x-8y.慧眼找错错正确答案:3x+2x=2-7.错正确答案:2x+8y-6x=2x-6x+8y
= -4x+8y.化简多项式交换两项位置时不改变项的符号;
解方程移项时必须改变项的符号.练习3例1 解方程 4x-15=9解: 移项,得4x=9+15.合并同类项,得4x=24.系数化为1,得x=6.练习4 解方程解:两边都加上15,得4x=9+15合并同类项,得4x=24系数化为1,得x=6移项实际上是利用等式的性质1,但是解题步骤更为简捷!例2 解方程解:移项,得合并同类项 ,得例2 解方程 解一元一次方程时,
一般把含未知数的项移
到方程的左边,常数项
移到方程的右边.系数化为1,得练习5 解方程例题3:解:移项,得:合并同类项,得:化系数为1,得:练习6 解下列一元一次方程1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。 3.移项要改变符号.2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).这节课我们学习了什么?移项拓展探究:解下列一元一次方程:谢谢你们认真听课!这是对老师最大的鼓励!
