华师大版数学八下 18.1.1平行四边形的性质 课件 (共24张PPT)
文档属性
| 名称 | 华师大版数学八下 18.1.1平行四边形的性质 课件 (共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 627.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
第1课时 平行四边形的性质定理1、2、3
华东师大版八年级数学下册
18.1 平行四边形的性质
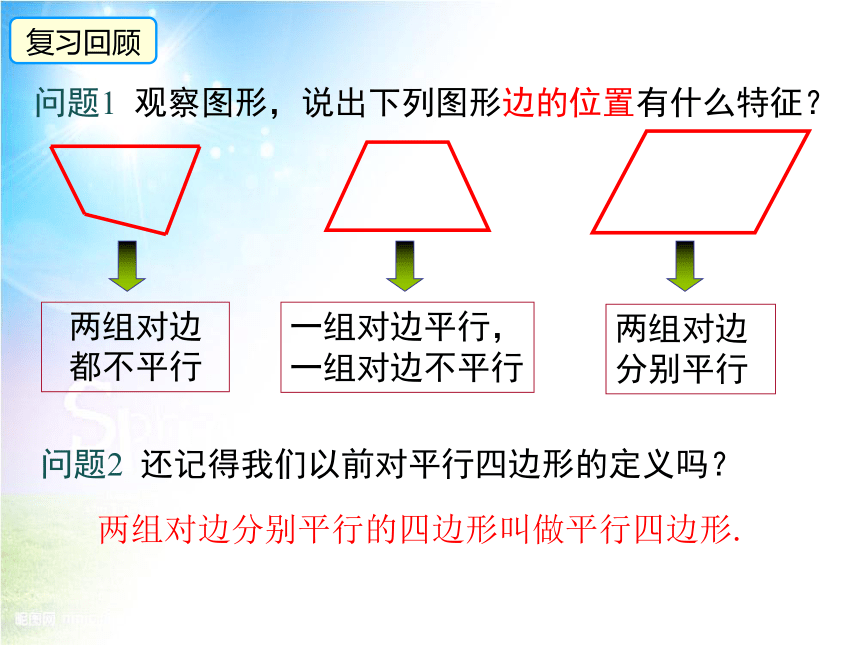
两组对边 都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 还记得我们以前对平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
复习回顾
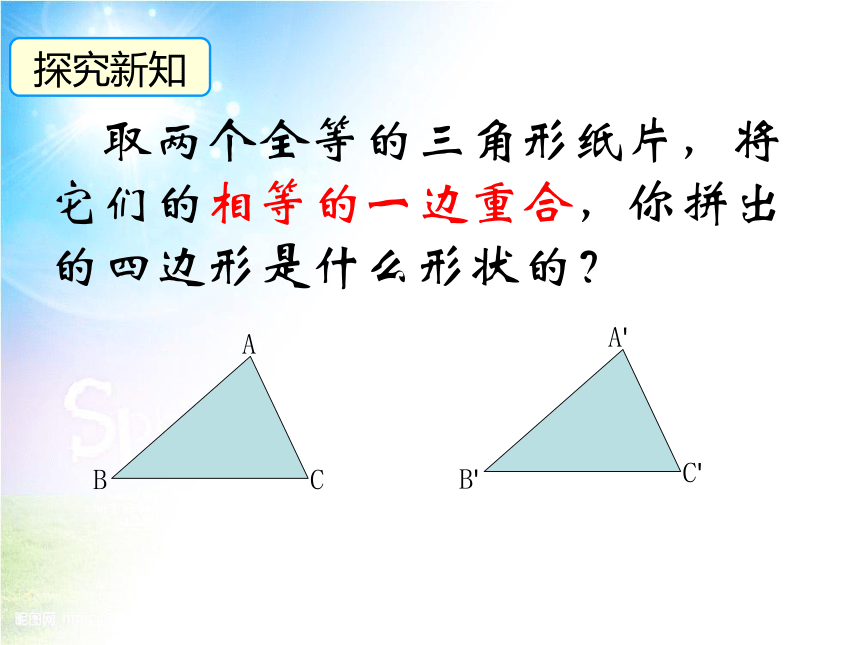
取两个全等的三角形纸片,将它们的相等的一边重合,你拼出的四边形是什么形状的?
探究新知
A
B
C
A'
B'
C'
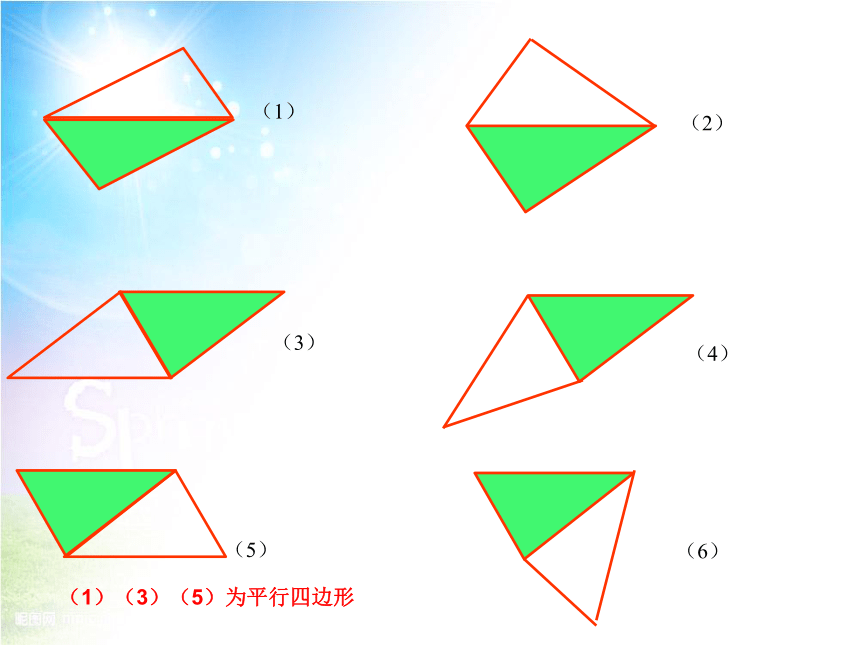
(1)
(2)
(3)
(4)
(5)
(6)
(1)(3)(5)为平行四边形
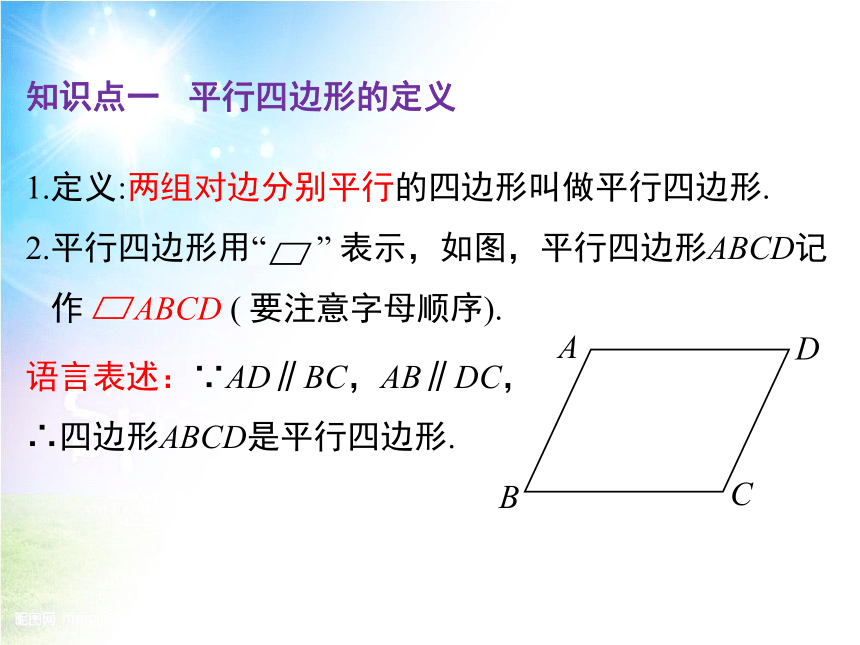
知识点一 平行四边形的定义
2.平行四边形用“ ” 表示,如图,平行四边形ABCD记
作 ABCD ( 要注意字母顺序).
1.定义:两组对边分别平行的四边形叫做平行四边形.
A
B
D
C
语言表述:∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
例1 如图,DC∥GH ∥ AB,DA∥ EF∥ CB,图中的平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
K
解:∵DC∥GH ∥ AB,DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有9个平行四边形,即 AEKG, ABHG,
AEFD, GKFD, BEKH, CHKF, BEFC,
CDGH, ABCD.
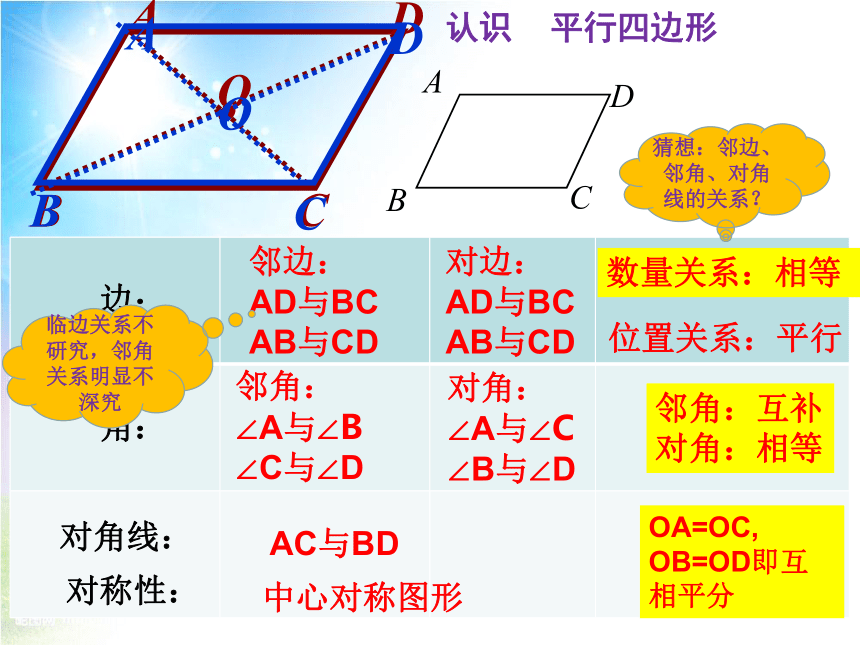
认识 平行四边形
A
B
D
C
边:
角:
对角线:
对边:
AD与BC
AB与CD
邻边:
AD与BC
AB与CD
邻角:
∠A与∠B
∠C与∠D
对角:
∠A与∠C
∠B与∠D
AC与BD
●
A
D
O
C
B
D
B
O
C
A
对称性:
中心对称图形
数量关系:相等
位置关系:平行
邻角:互补
对角:相等
临边关系不研究,邻角关系明显不深究
猜想:邻边、邻角、对角线的关系?
OA=OC,
OB=OD即互相平分
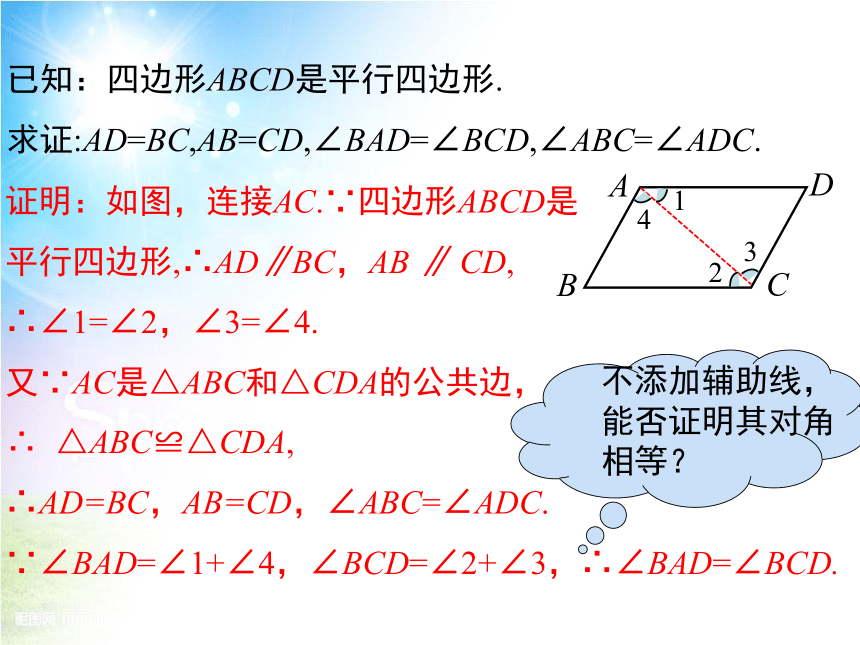
证明:如图,连接AC.∵四边形ABCD是
平行四边形,∴AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
不添加辅助线,能否证明其对角相等?
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
A
B
C
D
性质1、平行四边形的对边平行且相等
性质2、平行四边形的对角相等
归纳:平行四边形的性质
符号语言:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D.(平行四边形的对角相等)
A
B
C
D
试一试
1.如图,在□ABCD中.
(1)若∠A=130°,则∠B=______ ,∠C=______ ,
∠D=______.
(2)若AB=3,BC=5,则它的周长= ______.
2.如图,在□ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
B
E
C
D
A
50°
50°
130°
16
4
1
2
3
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
证一证
例 1 如图, ABCD 的对角线 AC 和 BD相交于点 O,△AOB 的周长为 15,AB = 6,那么对角线 AC 与 BD 的和是多少
A
B
C
D
O
解 在 ABCD 中,
∵AB = 6,AO + BO + AB = 15,
AO + BO = 15 – 6 = 9.
又∵AO = OC,BO = OD(平行四边形的对角线互相平分),
∴AC + BD
= 2AO + 2BO = 2(AO + BO) = 2×9 = 18.
变式练习:. 如图, ABCD 的对角线 AC 与 BD 相交点 O,∠ADB = 90°,OA = 6,OB = 3. 求 AD 和 AC 的长度.
解:∵四边形 ABCD 是平行四边形,
∴OA = OC = 6,OB = OD = 3
(平行四边形的对角线互相平分),
∴AC = OA + OC = 12.
∵ ∠ADB = 90°,
∴△ADO 为直角三角形.
∴AD = .
例2 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∵DE⊥AB,BF⊥CD
∴∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS),
∴AE=CF.
D
A
B
C
F
E
两条平行线间的距离相等.
m // n,AB、CD、EF垂直于 n,交 m于A、C、E,交n于B、D、F.
B
F
E
A
n
m
C
D
由平行四边形的性质易得AB=CD=EF
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线间的距离.
由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.
通过本课时的学习,需要我们掌握:
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行 对边相等
对角相等 邻角互补.
对角线互相平分
3.两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
4.平行四边是中心对称图形
随堂演练
1. 如图,在 ABCD 中,AC = 4cm,CD= 3 cm,BC = 5 cm,则 ABCD 的面积为________.
A
D
C
B
4
5
3
12 cm2
随堂演练
2. 在 ABCD 中, ∠A 与∠B 的度数之比为 4∶5,∠A =_____, ∠B =_____, ∠C =_____,∠D =_____.
A
B
C
D
80°
100°
80°
100°
随堂演练
3. 平行四边形的一条角平分线分对边为 3 和4 两部分,求平行四边形的周长.
A
B
D
C
E
1
2
3
解:如图,∵ ABCD 中,
AD∥BC,∴∠1 =∠3,
又∠1 =∠2,∴∠2 =∠3,∴AB = BE.
当 BE = 3 时,AB = BE = 3,
∴ ABCD 的周长为:
(AB + BC)×2 =(3 + 7)×2 = 20.
当 BE = 4 时,AB = BE = 4,
∴ ABCD 的周长为:
(AB + BC)×2 =(4 + 7)×2 = 22.
随堂演练
4. 如图,在 中,已知 AD = 8 cm,AB = 6 cm,DE 平分∠ADC 交 BC 边于点 E,则BE 的长为________.
2 cm
ABCD
平分线+平行线…………得出等腰三角形
随堂演练
5. 平行四边形两条对角线的长分别为 10,16,则它的边长 x 的取值范围是___________.
3<x<13
6. 平行四边形两条对角线的长分别为 10,16,则它的边长 x 的取值范围是___________.
3<x<13
随堂演练
7.(1) ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系?并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
证明:OE=OF,理由如下:
∵四边形ABCD为平行四边形,
∴OA=OC,AB∥CD
∵AB∥CD
∴∠1=∠2,∠EAO=∠OCF
∴⊿AEO≌⊿CFO
∴OE=OF
随堂演练
●
O
D
C
B
A
E
F
(2)
(2)在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
证明:OE=OF仍然成立,理由如下:
∵四边形ABCD为平行四边形,
∴OA=OC,AD∥BC
∵AD∥BC
∴∠E=∠F,
∵∠AOE=∠FOC
∴⊿AEO≌⊿CFO
∴OE=OF
第1课时 平行四边形的性质定理1、2、3
华东师大版八年级数学下册
18.1 平行四边形的性质
两组对边 都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
问题1 观察图形,说出下列图形边的位置有什么特征?
问题2 还记得我们以前对平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
复习回顾
取两个全等的三角形纸片,将它们的相等的一边重合,你拼出的四边形是什么形状的?
探究新知
A
B
C
A'
B'
C'
(1)
(2)
(3)
(4)
(5)
(6)
(1)(3)(5)为平行四边形
知识点一 平行四边形的定义
2.平行四边形用“ ” 表示,如图,平行四边形ABCD记
作 ABCD ( 要注意字母顺序).
1.定义:两组对边分别平行的四边形叫做平行四边形.
A
B
D
C
语言表述:∵AD∥BC,AB∥DC,
∴四边形ABCD是平行四边形.
例1 如图,DC∥GH ∥ AB,DA∥ EF∥ CB,图中的平行四边形有多少个?将它们表示出来.
D
A
B
C
H
G
F
E
K
解:∵DC∥GH ∥ AB,DA∥ EF∥ CB,
∴根据平行四边形的定义可以判定图中共有9个平行四边形,即 AEKG, ABHG,
AEFD, GKFD, BEKH, CHKF, BEFC,
CDGH, ABCD.
认识 平行四边形
A
B
D
C
边:
角:
对角线:
对边:
AD与BC
AB与CD
邻边:
AD与BC
AB与CD
邻角:
∠A与∠B
∠C与∠D
对角:
∠A与∠C
∠B与∠D
AC与BD
●
A
D
O
C
B
D
B
O
C
A
对称性:
中心对称图形
数量关系:相等
位置关系:平行
邻角:互补
对角:相等
临边关系不研究,邻角关系明显不深究
猜想:邻边、邻角、对角线的关系?
OA=OC,
OB=OD即互相平分
证明:如图,连接AC.∵四边形ABCD是
平行四边形,∴AD∥BC,AB ∥ CD,
∴∠1=∠2,∠3=∠4.
又∵AC是△ABC和△CDA的公共边,
∴ △ABC≌△CDA,
∴AD=BC,AB=CD,∠ABC=∠ADC.
∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,∴∠BAD=∠BCD.
A
B
C
D
1
4
3
2
已知:四边形ABCD是平行四边形.
求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.
不添加辅助线,能否证明其对角相等?
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
A
B
C
D
性质1、平行四边形的对边平行且相等
性质2、平行四边形的对角相等
归纳:平行四边形的性质
符号语言:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.(平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D.(平行四边形的对角相等)
A
B
C
D
试一试
1.如图,在□ABCD中.
(1)若∠A=130°,则∠B=______ ,∠C=______ ,
∠D=______.
(2)若AB=3,BC=5,则它的周长= ______.
2.如图,在□ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC= .
B
E
C
D
A
50°
50°
130°
16
4
1
2
3
A
C
D
B
O
已知:如图: ABCD的对角线AC、BD
相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
证一证
例 1 如图, ABCD 的对角线 AC 和 BD相交于点 O,△AOB 的周长为 15,AB = 6,那么对角线 AC 与 BD 的和是多少
A
B
C
D
O
解 在 ABCD 中,
∵AB = 6,AO + BO + AB = 15,
AO + BO = 15 – 6 = 9.
又∵AO = OC,BO = OD(平行四边形的对角线互相平分),
∴AC + BD
= 2AO + 2BO = 2(AO + BO) = 2×9 = 18.
变式练习:. 如图, ABCD 的对角线 AC 与 BD 相交点 O,∠ADB = 90°,OA = 6,OB = 3. 求 AD 和 AC 的长度.
解:∵四边形 ABCD 是平行四边形,
∴OA = OC = 6,OB = OD = 3
(平行四边形的对角线互相平分),
∴AC = OA + OC = 12.
∵ ∠ADB = 90°,
∴△ADO 为直角三角形.
∴AD = .
例2 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:AE=CF.
证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∵DE⊥AB,BF⊥CD
∴∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS),
∴AE=CF.
D
A
B
C
F
E
两条平行线间的距离相等.
m // n,AB、CD、EF垂直于 n,交 m于A、C、E,交n于B、D、F.
B
F
E
A
n
m
C
D
由平行四边形的性质易得AB=CD=EF
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线间的距离.
由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.
通过本课时的学习,需要我们掌握:
1、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
2、平行四边形的性质:对边平行 对边相等
对角相等 邻角互补.
对角线互相平分
3.两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
4.平行四边是中心对称图形
随堂演练
1. 如图,在 ABCD 中,AC = 4cm,CD= 3 cm,BC = 5 cm,则 ABCD 的面积为________.
A
D
C
B
4
5
3
12 cm2
随堂演练
2. 在 ABCD 中, ∠A 与∠B 的度数之比为 4∶5,∠A =_____, ∠B =_____, ∠C =_____,∠D =_____.
A
B
C
D
80°
100°
80°
100°
随堂演练
3. 平行四边形的一条角平分线分对边为 3 和4 两部分,求平行四边形的周长.
A
B
D
C
E
1
2
3
解:如图,∵ ABCD 中,
AD∥BC,∴∠1 =∠3,
又∠1 =∠2,∴∠2 =∠3,∴AB = BE.
当 BE = 3 时,AB = BE = 3,
∴ ABCD 的周长为:
(AB + BC)×2 =(3 + 7)×2 = 20.
当 BE = 4 时,AB = BE = 4,
∴ ABCD 的周长为:
(AB + BC)×2 =(4 + 7)×2 = 22.
随堂演练
4. 如图,在 中,已知 AD = 8 cm,AB = 6 cm,DE 平分∠ADC 交 BC 边于点 E,则BE 的长为________.
2 cm
ABCD
平分线+平行线…………得出等腰三角形
随堂演练
5. 平行四边形两条对角线的长分别为 10,16,则它的边长 x 的取值范围是___________.
3<x<13
6. 平行四边形两条对角线的长分别为 10,16,则它的边长 x 的取值范围是___________.
3<x<13
随堂演练
7.(1) ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系?并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
证明:OE=OF,理由如下:
∵四边形ABCD为平行四边形,
∴OA=OC,AB∥CD
∵AB∥CD
∴∠1=∠2,∠EAO=∠OCF
∴⊿AEO≌⊿CFO
∴OE=OF
随堂演练
●
O
D
C
B
A
E
F
(2)
(2)在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
●
●
证明:OE=OF仍然成立,理由如下:
∵四边形ABCD为平行四边形,
∴OA=OC,AD∥BC
∵AD∥BC
∴∠E=∠F,
∵∠AOE=∠FOC
∴⊿AEO≌⊿CFO
∴OE=OF
