5.2.2等差数列前n项和课件-2021-2022学年高二下学期数学人教B版(2019)选择性必修第三册(共18张PPT)
文档属性
| 名称 | 5.2.2等差数列前n项和课件-2021-2022学年高二下学期数学人教B版(2019)选择性必修第三册(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 983.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-10 22:08:30 | ||
图片预览






文档简介
(共18张PPT)
等差数列前n项和(一)
复习回顾
3.等差数列通项公式
若
,则
4.等差数列性质:
1.数列{an}的前n项和
2.Sn与an的关系
学习目标:
1.掌握等差数列的通项公式和前项和公式;
2.掌握数列 的前n项和 与 之间的关系;
3.理解等差数列前n项和与二次函数间的关系,并会简单应用。
为了达到更好的音响和观赏效果,很多剧场的座位都是排成圆弧形的,如左图所示:
如果某公司要为一个类似的剧场定做椅子,而且剧场座位的排列规律是:第1排36个,以后每一排比前一排多6个,共有8排.你能帮这个公司算出共需要多少椅子吗
1.本例中每排椅子数有什么规律?
情境与问题
2.共需要多少个椅子,实际上是求什么?
3.怎样求前8项和?如果项数多,该怎么求?
建筑工地上堆放着一些钢管,最上面一层有4根,下面每一层比上一层多放一根,共8层.
(1)在不逐个相加的前提下,你能想办法算出这些钢管共有多少根吗
(2)你能得出一般等差数列前n项和的公式吗
这些钢管,从上到下每一层的数量构成一个等差数列
这个数列的首项为a1=4,公差d=1,而且该数列共有8项,第8项为a8=4+(8-1)×1=11 设想在钢管旁边再放同样多数量的钢管,但是倒过来放置,如下图所示.
所以S8=
(4+11)×8
?
?
首项
末项
?
总
和
?
项数
=60
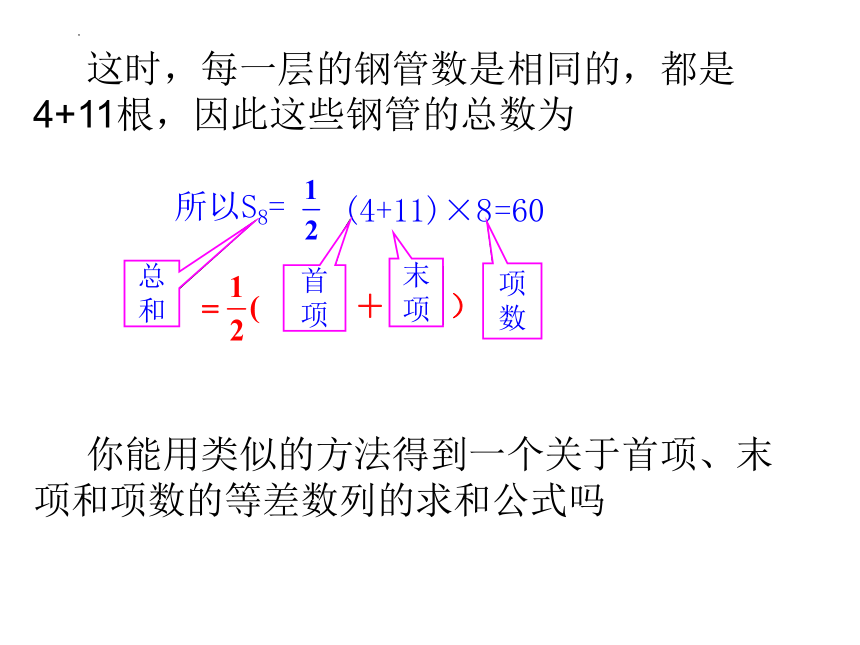
这时,每一层的钢管数是相同的,都是4+11根,因此这些钢管的总数为
你能用类似的方法得到一个关于首项、末项和项数的等差数列的求和公式吗
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
①
②
公式一
①②相加得
根据等差数列的性质有
公式一
上述等差数列前项求和公式与首项n和第n项 有关,你能将其改成与公差d有关的形式吗?
公式二
由此可知,前述情境与问题中椅子总数为
例1.已知等差数列 的公差为2,且a20=29,求这个等差数列前20项和S20
方法总结:结合等差数列的通项公式,对于a1,d,n,an,sn五个量,知三求二
由等差数列的通项公式可得:
例2.求等差数列5,12,19,26,...,201,208
的各项之和.
可以看出,所求数列是公差为7的等差数列.
设共有n项,则208=5+(n-1)×7,解得n=30.因此各项之和为
方法总结:本题难点在于如何利用等差数列通项公式求出项数,还可用末项减去首项,除以公差加1得到。即
方法总结:本题考查Sn与an的关系
注意不要忽略n=1时的验证
总结:
上式可写成Sn=An2+Bn
上式可写成Sn=An2+Bn
一、等差数列的前n项和公式
小结:
二、思想方法
倒序相加法
Thank You
等差数列前n项和(一)
复习回顾
3.等差数列通项公式
若
,则
4.等差数列性质:
1.数列{an}的前n项和
2.Sn与an的关系
学习目标:
1.掌握等差数列的通项公式和前项和公式;
2.掌握数列 的前n项和 与 之间的关系;
3.理解等差数列前n项和与二次函数间的关系,并会简单应用。
为了达到更好的音响和观赏效果,很多剧场的座位都是排成圆弧形的,如左图所示:
如果某公司要为一个类似的剧场定做椅子,而且剧场座位的排列规律是:第1排36个,以后每一排比前一排多6个,共有8排.你能帮这个公司算出共需要多少椅子吗
1.本例中每排椅子数有什么规律?
情境与问题
2.共需要多少个椅子,实际上是求什么?
3.怎样求前8项和?如果项数多,该怎么求?
建筑工地上堆放着一些钢管,最上面一层有4根,下面每一层比上一层多放一根,共8层.
(1)在不逐个相加的前提下,你能想办法算出这些钢管共有多少根吗
(2)你能得出一般等差数列前n项和的公式吗
这些钢管,从上到下每一层的数量构成一个等差数列
这个数列的首项为a1=4,公差d=1,而且该数列共有8项,第8项为a8=4+(8-1)×1=11 设想在钢管旁边再放同样多数量的钢管,但是倒过来放置,如下图所示.
所以S8=
(4+11)×8
?
?
首项
末项
?
总
和
?
项数
=60
这时,每一层的钢管数是相同的,都是4+11根,因此这些钢管的总数为
你能用类似的方法得到一个关于首项、末项和项数的等差数列的求和公式吗
已知等差数列{ an }的首项为a1,项数是n,第n项为an,求前n项和Sn .
①
②
公式一
①②相加得
根据等差数列的性质有
公式一
上述等差数列前项求和公式与首项n和第n项 有关,你能将其改成与公差d有关的形式吗?
公式二
由此可知,前述情境与问题中椅子总数为
例1.已知等差数列 的公差为2,且a20=29,求这个等差数列前20项和S20
方法总结:结合等差数列的通项公式,对于a1,d,n,an,sn五个量,知三求二
由等差数列的通项公式可得:
例2.求等差数列5,12,19,26,...,201,208
的各项之和.
可以看出,所求数列是公差为7的等差数列.
设共有n项,则208=5+(n-1)×7,解得n=30.因此各项之和为
方法总结:本题难点在于如何利用等差数列通项公式求出项数,还可用末项减去首项,除以公差加1得到。即
方法总结:本题考查Sn与an的关系
注意不要忽略n=1时的验证
总结:
上式可写成Sn=An2+Bn
上式可写成Sn=An2+Bn
一、等差数列的前n项和公式
小结:
二、思想方法
倒序相加法
Thank You
