人教版八年级数学下册 第18章 平行四边形 单元训练 (word版含答案)
文档属性
| 名称 | 人教版八年级数学下册 第18章 平行四边形 单元训练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 06:31:55 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学下册
第18章《平行四边形》单元训练
一、单选题
1.下列命题错误的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
2.如图,将平行四边形ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF B.AB=EF C.AE=AF D.AF=BE
3.如图,的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.12
4.如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )
A.3:4 B.5:8 C.9: 16 D.1:2
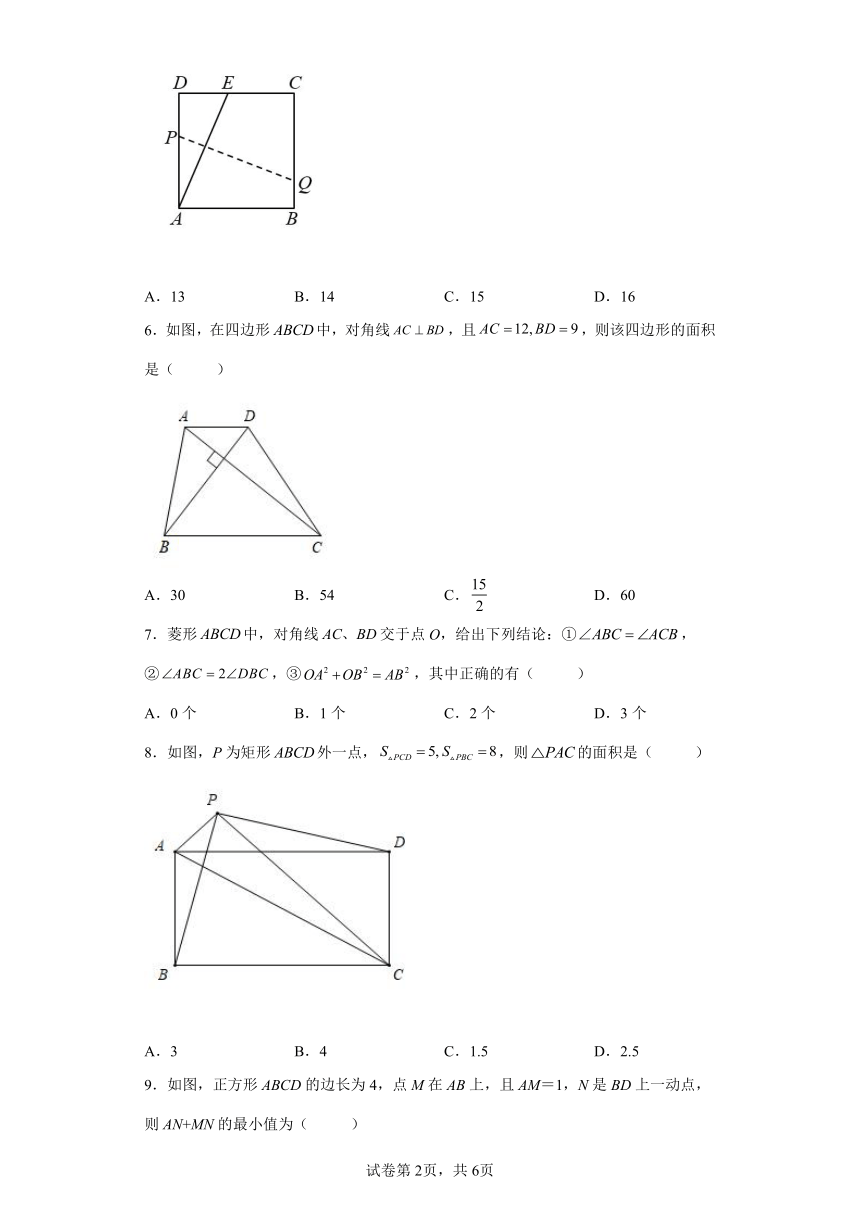
5.如图,将一边长为12的正方形纸片的顶点A折叠至边上的点E,使,若折痕为,则的长为( )
A.13 B.14 C.15 D.16
6.如图,在四边形中,对角线,且,则该四边形的面积是( )
A.30 B.54 C. D.60
7.菱形中,对角线交于点O,给出下列结论:①,②,③,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
8.如图,P为矩形外一点,,则的面积是( )
A.3 B.4 C.1.5 D.2.5
9.如图,正方形ABCD的边长为4,点M在AB上,且AM=1,N是BD上一动点,则AN+MN的最小值为( )
A.4 B. C.5 D.4
10.一次数学课上,老师请同学们在一张长为18厘米.宽为16厘米的长方形纸板上.剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与长方形的一个顶点重合,其它两个顶点在长方形的边上,剪下的等腰三角形的面积为( )
A.50 B.50或40 C.50或40或30 D.50或30或20
二、填空题
11.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为,则这个平行四边形的各内角的度数为_________.
12.点A、B、C、D在同一平面内,从(1)AB//CD,(2)AB=CD,(3)BC//AD,(4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有_______种
13.如图,正方形中,E为边上一点,平分交于F,若,则_________.
14.如图,E为矩形纸片的边上一点,将纸片沿折叠,使点D落在边的中垂线上,若,则的长为________.
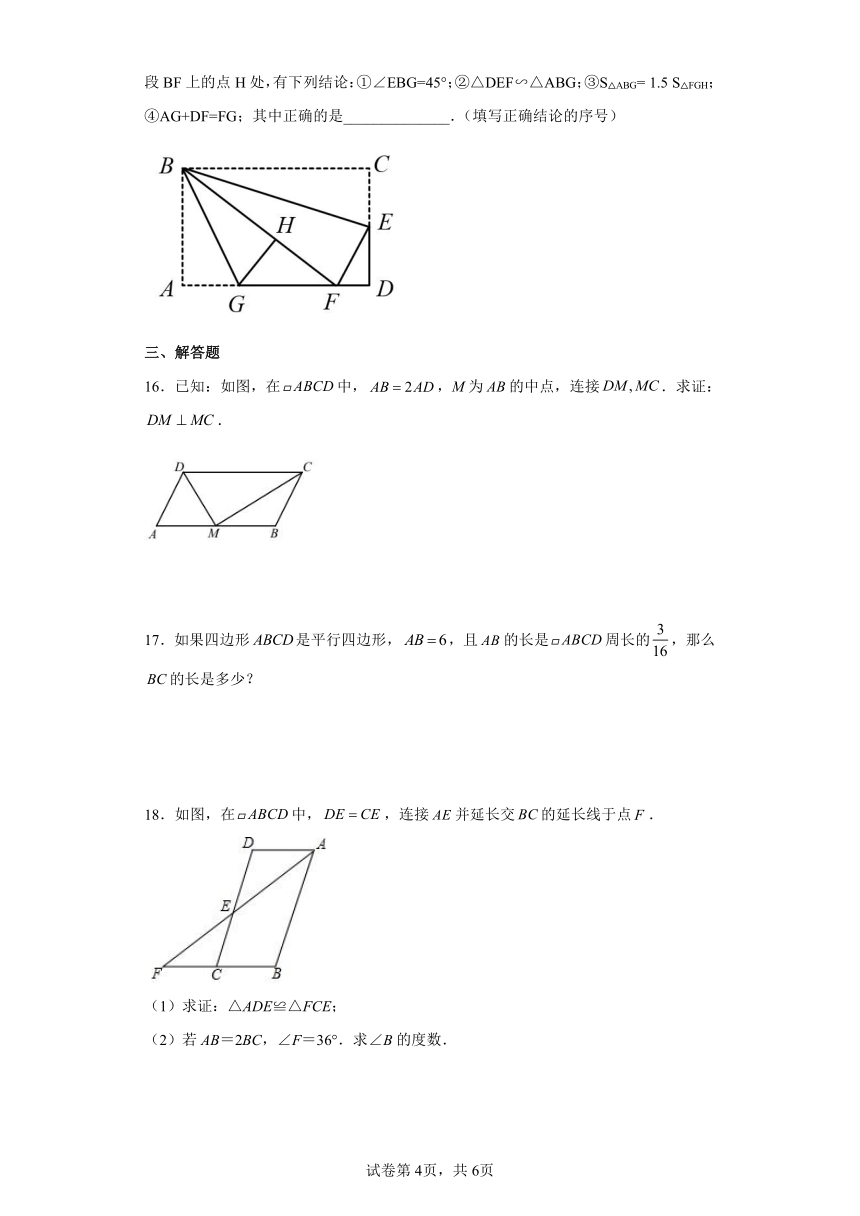
15.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折 叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG= 1.5 S△FGH;④AG+DF=FG;其中正确的是______________.(填写正确结论的序号)
三、解答题
16.已知:如图,在中,,M为的中点,连接.求证:.
17.如果四边形是平行四边形,,且的长是周长的,那么的长是多少?
18.如图,在中,,连接并延长交的延长线于点.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
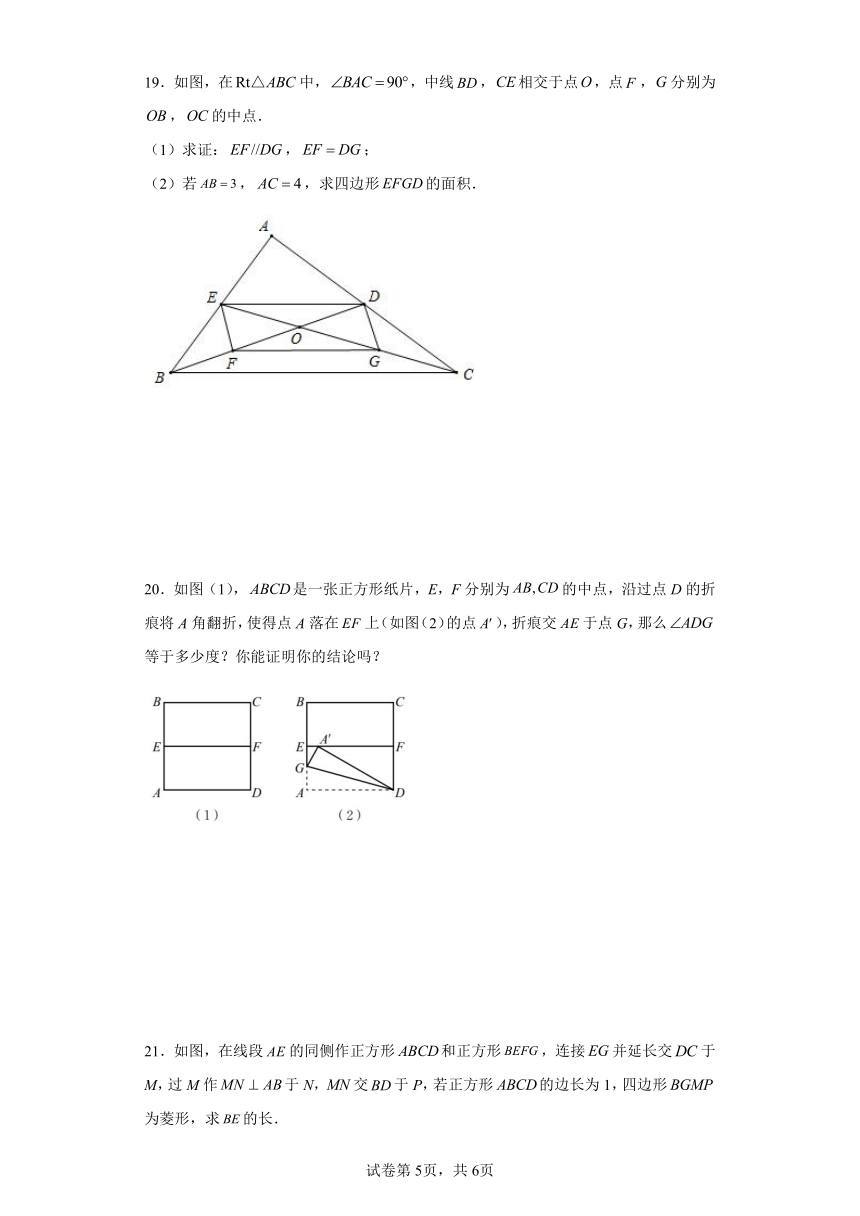
19.如图,在中,,中线,相交于点,点,分别为,的中点.
(1)求证:,;
(2)若,,求四边形的面积.
20.如图(1),是一张正方形纸片,E,F分别为的中点,沿过点D的折痕将A角翻折,使得点A落在上(如图(2)的点),折痕交于点G,那么等于多少度?你能证明你的结论吗?
21.如图,在线段的同侧作正方形和正方形,连接并延长交于M,过M作于N,交于P,若正方形的边长为1,四边形为菱形,求的长.
22.已知:如图,在中,,的垂直平分线分别交和于点D,E,点F在的延长线上,且.求证:四边形是菱形.
23.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若∠BDE=15°,求∠DOE;
(3)在(2)的条件下,若AB=2,求△BOE的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.C
3.C
4.B
5.A
6.B
7.C
8.A
9.C
10.C
11.
12.4
13.8
14.2
15.①③④
16
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠CDM=∠AMD,∠DCM=∠BMC,
∵AB=2AD,M为AB的中点,
∴AD=AM=BM=BC,
∴∠ADM=∠AMD,∠BCM=∠BMC,
∴∠ADM=∠CDM=∠ADC,∠DCM=∠BCM=∠BCD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠CDM+∠DCM=90°,
∴∠DMC=90°,
即DM⊥MC.
17.
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ,
∴四边形ABCD周长为:,
∴AB+BC=,
∴.
答:的长是10.
18.
(1)证明:∵四边形ABCD是平行四边形,
∴ADBC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,,
∴△ADE≌△FCE(ASA);
(2)解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°2×36°=108°.
19.
(1)证明:∵点,分别是,的中点,
∴,.
∵点,分别是,的中点,
∴,.
∴,.
∴四边形是平行四边形.
∴,;
(2)解:∵,
∴.
又∵,
∴.
∵,,
∵,
∵点是中点,
∴.
∴.
∴四边形的面积.
20
解:如图,连接,
四边形是正方形,
,,,
、分别为、的中点,
,
,
∵,,,
四边形是矩形,
,
,
又∵点是的中点,
∴EF垂直平分CD,
∴,
∵折叠,
∴,,
又∵,
∴,
为等边三角形,
,
,
.
21.
证明:∵四边形ABCD和四边形BEFG均为正方形,四边形为菱形,
∴DC=BC, ,∠C=∠GBE=90°,∠CDB=∠CBD=45°,MGBD,
∴∠CMG=∠CDB=45°,∠CGM=∠CBD=45°,
∴∠CMG=∠CGM,
∴CM=CG,
∴DM=BG
设正方形BEFG的边长为x,
∵BGMP是菱形,
则DM=BG=MG=x,MC=CG=1 x,
在Rt△MCG中,有 ,
即,
解这个方程得, ,
∵BE<AB,
∴舍去.
∴BE=MG=.
22.
证明:∵是的垂直平分线,
,BE=CE,
∴,
,,
∴,
∴,
为等边三角形,
∴,
又∵,
∴,
,
∴,
∴,
又∵,
为等边三角形,
∴,
∴,
∴四边形为菱形.
23.
解:(1)∵ADBC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形.
(2)由(1)可得:AO=CO,BO=DO,AC=BD,
∴OD=OC,
∵DE平分∠ADC,
∴∠CDE=45°,
∴△DCE是等腰直角三角形,
∴∠DEC=45°,CD=CE,
∵∠BDE=15°,
∴∠DBC=∠ADB=45°-15°=30°,
∴∠BDC=60°,又OD=OC,
∴△OCD是等边三角形,
∴OC=CD=CE,∠DCO=∠COD=60°,
∴∠OCE=30°,
∴∠COE=∠CEO=(180°-30°)÷2=75°,
∴∠DOE=∠COD+∠COE=60°+75°=135°;
(3)作OF⊥BC于F.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=CD=1,
∵EC=CD=AB=2,
∴AC=BD=4,
∴BC==,
∴BE=BC-CE=-2,
∴△BOE的面积= .
答案第1页,共2页
答案第1页,共2页
第18章《平行四边形》单元训练
一、单选题
1.下列命题错误的是( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行,另一组对边相等的四边形是平行四边形
D.对角线互相平分的四边形是平行四边形
2.如图,将平行四边形ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF B.AB=EF C.AE=AF D.AF=BE
3.如图,的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.12
4.如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )
A.3:4 B.5:8 C.9: 16 D.1:2
5.如图,将一边长为12的正方形纸片的顶点A折叠至边上的点E,使,若折痕为,则的长为( )
A.13 B.14 C.15 D.16
6.如图,在四边形中,对角线,且,则该四边形的面积是( )
A.30 B.54 C. D.60
7.菱形中,对角线交于点O,给出下列结论:①,②,③,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
8.如图,P为矩形外一点,,则的面积是( )
A.3 B.4 C.1.5 D.2.5
9.如图,正方形ABCD的边长为4,点M在AB上,且AM=1,N是BD上一动点,则AN+MN的最小值为( )
A.4 B. C.5 D.4
10.一次数学课上,老师请同学们在一张长为18厘米.宽为16厘米的长方形纸板上.剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与长方形的一个顶点重合,其它两个顶点在长方形的边上,剪下的等腰三角形的面积为( )
A.50 B.50或40 C.50或40或30 D.50或30或20
二、填空题
11.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为,则这个平行四边形的各内角的度数为_________.
12.点A、B、C、D在同一平面内,从(1)AB//CD,(2)AB=CD,(3)BC//AD,(4)BC=AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有_______种
13.如图,正方形中,E为边上一点,平分交于F,若,则_________.
14.如图,E为矩形纸片的边上一点,将纸片沿折叠,使点D落在边的中垂线上,若,则的长为________.
15.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折 叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG= 1.5 S△FGH;④AG+DF=FG;其中正确的是______________.(填写正确结论的序号)
三、解答题
16.已知:如图,在中,,M为的中点,连接.求证:.
17.如果四边形是平行四边形,,且的长是周长的,那么的长是多少?
18.如图,在中,,连接并延长交的延长线于点.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
19.如图,在中,,中线,相交于点,点,分别为,的中点.
(1)求证:,;
(2)若,,求四边形的面积.
20.如图(1),是一张正方形纸片,E,F分别为的中点,沿过点D的折痕将A角翻折,使得点A落在上(如图(2)的点),折痕交于点G,那么等于多少度?你能证明你的结论吗?
21.如图,在线段的同侧作正方形和正方形,连接并延长交于M,过M作于N,交于P,若正方形的边长为1,四边形为菱形,求的长.
22.已知:如图,在中,,的垂直平分线分别交和于点D,E,点F在的延长线上,且.求证:四边形是菱形.
23.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若∠BDE=15°,求∠DOE;
(3)在(2)的条件下,若AB=2,求△BOE的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
2.C
3.C
4.B
5.A
6.B
7.C
8.A
9.C
10.C
11.
12.4
13.8
14.2
15.①③④
16
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠CDM=∠AMD,∠DCM=∠BMC,
∵AB=2AD,M为AB的中点,
∴AD=AM=BM=BC,
∴∠ADM=∠AMD,∠BCM=∠BMC,
∴∠ADM=∠CDM=∠ADC,∠DCM=∠BCM=∠BCD,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠CDM+∠DCM=90°,
∴∠DMC=90°,
即DM⊥MC.
17.
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ,
∴四边形ABCD周长为:,
∴AB+BC=,
∴.
答:的长是10.
18.
(1)证明:∵四边形ABCD是平行四边形,
∴ADBC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,,
∴△ADE≌△FCE(ASA);
(2)解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°2×36°=108°.
19.
(1)证明:∵点,分别是,的中点,
∴,.
∵点,分别是,的中点,
∴,.
∴,.
∴四边形是平行四边形.
∴,;
(2)解:∵,
∴.
又∵,
∴.
∵,,
∵,
∵点是中点,
∴.
∴.
∴四边形的面积.
20
解:如图,连接,
四边形是正方形,
,,,
、分别为、的中点,
,
,
∵,,,
四边形是矩形,
,
,
又∵点是的中点,
∴EF垂直平分CD,
∴,
∵折叠,
∴,,
又∵,
∴,
为等边三角形,
,
,
.
21.
证明:∵四边形ABCD和四边形BEFG均为正方形,四边形为菱形,
∴DC=BC, ,∠C=∠GBE=90°,∠CDB=∠CBD=45°,MGBD,
∴∠CMG=∠CDB=45°,∠CGM=∠CBD=45°,
∴∠CMG=∠CGM,
∴CM=CG,
∴DM=BG
设正方形BEFG的边长为x,
∵BGMP是菱形,
则DM=BG=MG=x,MC=CG=1 x,
在Rt△MCG中,有 ,
即,
解这个方程得, ,
∵BE<AB,
∴舍去.
∴BE=MG=.
22.
证明:∵是的垂直平分线,
,BE=CE,
∴,
,,
∴,
∴,
为等边三角形,
∴,
又∵,
∴,
,
∴,
∴,
又∵,
为等边三角形,
∴,
∴,
∴四边形为菱形.
23.
解:(1)∵ADBC,
∴∠ABC+∠BAD=180°,
∵∠ABC=90°,
∴∠BAD=90°,
∴∠BAD=∠ABC=∠ADC=90°,
∴四边形ABCD是矩形.
(2)由(1)可得:AO=CO,BO=DO,AC=BD,
∴OD=OC,
∵DE平分∠ADC,
∴∠CDE=45°,
∴△DCE是等腰直角三角形,
∴∠DEC=45°,CD=CE,
∵∠BDE=15°,
∴∠DBC=∠ADB=45°-15°=30°,
∴∠BDC=60°,又OD=OC,
∴△OCD是等边三角形,
∴OC=CD=CE,∠DCO=∠COD=60°,
∴∠OCE=30°,
∴∠COE=∠CEO=(180°-30°)÷2=75°,
∴∠DOE=∠COD+∠COE=60°+75°=135°;
(3)作OF⊥BC于F.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=CD=1,
∵EC=CD=AB=2,
∴AC=BD=4,
∴BC==,
∴BE=BC-CE=-2,
∴△BOE的面积= .
答案第1页,共2页
答案第1页,共2页
