4.1树与二叉树课件-2021-2022学年浙教版(2019)高中信息技术选修1(23张PPT)
文档属性
| 名称 | 4.1树与二叉树课件-2021-2022学年浙教版(2019)高中信息技术选修1(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 352.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-04-10 22:29:46 | ||
图片预览







文档简介
(共23张PPT)
4.1 树与二叉树
总经理
技术部
财务部
人事部
零售部
采购部
项目部
运营部
管理部
售后部
门店一
门店二
门店三
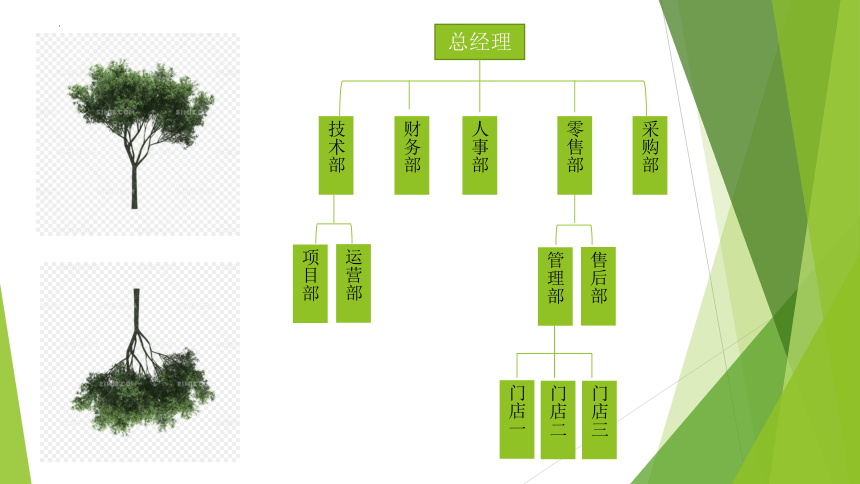
树形结构在现实世界中广泛存在,如上图所示的公司内部
管理的组织关系图就可以用树形结构来表示。树在计算机
领域中也有广泛应用,在编译系统中,用树表示源程序的
语法结构。在数据库系统中,树形结构是数据库层次模型
的基础,也是各种索引和目录的主要组织形式。
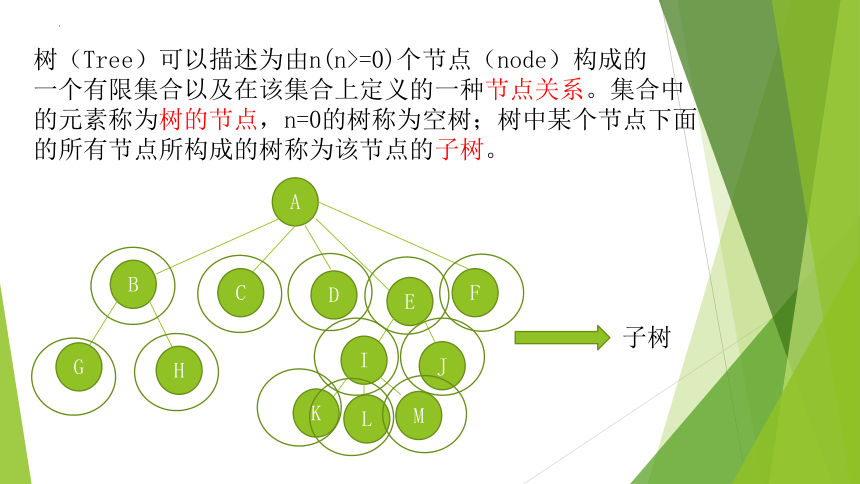
树(Tree)可以描述为由n(n>=0)个节点(node)构成的
一个有限集合以及在该集合上定义的一种节点关系。集合中
的元素称为树的节点,n=0的树称为空树;树中某个节点下面
的所有节点所构成的树称为该节点的子树。
A
B
G
H
C
D
E
F
I
J
K
L
M
子树
节点的度:树的一个节点所拥有的子树个数称为该节点的度。
树的度:最大节点的度称为树的度。
节点的度和树的度共同体现了树的宽度,也就是体现了节点
的分支数和树的发散程度。
线性表其实是一种特殊的树状结构,它的度为1。
树的两个节点之间如果有一条边连接,那么称这两个节点
之间存在一条边;对于一棵具有n个节点的树,它有n-1条边。
A
B
G
H
C
D
E
F
I
J
K
L
M
A节点的度为___________,B节点的度为__________,
I节点的度为__________。
该树的度为____________。
5
2
3
5
该树共有____________个节点、________条边。
13
12
在树形结构中,没有前驱的节点称为根节点(Root),
又称为开始节点。度为0的节点称为叶子节点(Leaf),它
又称为终端节点。树中度不为0的节点称为分支节点或者称
为非终端节点,除根节点外的分支节点统称为内部节点。
在上图中,节点A是根节点,节点G、H、C、D、K、L、M、
J、F都是叶子节点。
在树形结构中,对于两个以边直接连接的节点,上端节点
称为下端节点的父节点或双亲节点(Parent)。相应地,
下端节点称为上端节点的孩子节点(Child)。
A
B
G
H
C
D
E
F
I
J
K
L
M
节点K、L、M都是节点I的孩子节点
节点B是节点G、H的父节点
节点G、H是兄弟节点
树中节点的层数(Level)从根开始计算,根的层数为1,
其余节点的层数等于其父节点的层数加1。树中节点的最大
层数称为树的高度或深度(Depth)。
A
B
G
H
C
D
E
F
I
J
K
M
L
树的高度为4
节点G、H、I、J都在
第3层。
树形结构是比较复杂的非线性结构,在有多个节点
(节点个数>1)的树形结构中,它只有一个没有前驱、
只有后继的根节点,可以有多个没有后继、只有前驱的
叶子节点,其余的节点都只有一个直接前驱和多个直接后继。
二叉树
树的形态有很多,在实际的使用过程中,需要对树的形态
进一步地进行约束和简化,以便于设计和操作。二叉树是树形
结构的一个重要类型,在实际应用中,许多问题抽象出来的
数据结构往往就是二叉树的形式。
在猜数字游戏中,甲方事先在纸上写出一个100以内的正整
数,让乙方猜,乙方每猜一次,甲方都会告诉乙方“猜大了”
或是“猜小了”,直至猜出正确结果。
乙方如果采取“折半”的策略进行猜数字,就一定能
够在7次以内猜对结果,具体过程可以抽象成下图的二叉树结构。
50
25
12
37
6
18
31
43
75
62
56
68
88
82
96
小
小
小
小
小
小
小
大
大
大
大
大
大
大
二叉树的概念
二叉树(Binary Tree)是一个具有n(n>=0)个节点的有限
集合。当n=0时,二叉树是一棵空树;当n≠0时,则是一棵由
根节点和两棵互不相交的、分别称作这个根节点的左子树和右
子树组成的二叉树,由于左、右子树也是二叉树,因此子树也
可以是空树。
A
B
D
G
E
H
C
F
二叉树所有节点的度都小于或者等于2,
这给二叉树的操作带来了很大的方便。
一棵二叉树有5种可能的形态,如下图所示,从左到右
分别是:①空二叉树;②只有根节点的单点树;③只有
根节点和左子树;④只要根节点和右子树;⑤左右子树
均非空。
①
②
③
④
⑤
完全二叉树
这一类二叉树至多只有最下面两层中的节点度数小于2,
且最下面一层的叶子节点都依次排列在该层的最左边位置。
A
B
D
E
H
I
J
C
F
G
二叉树的性质
二叉树有很多性质,作为重要的数据结构,二叉树最重要
的性质就是树的高度和树中可以容纳的最大节点个数之间的
关系,主要有:
①二叉树的第k层上最多有2k-1(k>=1)个节点。
当k=1时,只有1(20=1)个根节点;当k=2时,由于节点的度
最大为2,因此,第2层的节点数最多有2(21=2)个节点。依次
推出,第k层上最多有2k-1个节点。
②深度为k的二叉树最多有2k-1(k>=1)个节点。
第1层至第k层上的最大节点数相加的结果是:20+21+…+2k-1=2k-1
因此2k-1是深度为k的二叉树的最多节点总数。
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子节点(度为
0的节点)数为n0,则n0=n2+1。
假设度为0,1和2的节点数分别是n0,n1和n2,则二叉树中
总的节点数n=n0+n1+n2。
在二叉树的所有节点中,除了根节点没有前驱外,每个节点均有且
只有一个前驱节点,因此有n个节点的二叉树的总边数为n-1条。
根据度的定义,二叉树的总边数与度之间的关系:n-1=0*n0+1*n1+2*n2,
结合上述两个等式,可以得出n0=n2+1。
甲
乙
在甲树上,度为2的节点数是1,度为1的节点数是1,叶子节点数
为2;在乙树上,度为2的节点数是2,度为1的节点数是1,叶子
节点数为3。
二叉树在实际应用中非常广泛,如基于二叉树的查找方法
(二叉排序树查找),具有较高的查找效率,还能够在查找
表中进行数据插入和删除等动态查找操作。
最优二叉树(又称哈夫曼树,Huffman Tree)广泛应用于编码
和决策等方面。
练一练
1.一棵度为3,深度为4的树的节点个数至多为:
A.31
B.32
C.40
D.42
C
2.在一棵度为2的树中,度为2的节点数为15,度为1的节点数
为30,则叶子节点(度为0的节点)的个数为:
A.15
B.16
C.17
D.47
B
谢 谢
4.1 树与二叉树
总经理
技术部
财务部
人事部
零售部
采购部
项目部
运营部
管理部
售后部
门店一
门店二
门店三
树形结构在现实世界中广泛存在,如上图所示的公司内部
管理的组织关系图就可以用树形结构来表示。树在计算机
领域中也有广泛应用,在编译系统中,用树表示源程序的
语法结构。在数据库系统中,树形结构是数据库层次模型
的基础,也是各种索引和目录的主要组织形式。
树(Tree)可以描述为由n(n>=0)个节点(node)构成的
一个有限集合以及在该集合上定义的一种节点关系。集合中
的元素称为树的节点,n=0的树称为空树;树中某个节点下面
的所有节点所构成的树称为该节点的子树。
A
B
G
H
C
D
E
F
I
J
K
L
M
子树
节点的度:树的一个节点所拥有的子树个数称为该节点的度。
树的度:最大节点的度称为树的度。
节点的度和树的度共同体现了树的宽度,也就是体现了节点
的分支数和树的发散程度。
线性表其实是一种特殊的树状结构,它的度为1。
树的两个节点之间如果有一条边连接,那么称这两个节点
之间存在一条边;对于一棵具有n个节点的树,它有n-1条边。
A
B
G
H
C
D
E
F
I
J
K
L
M
A节点的度为___________,B节点的度为__________,
I节点的度为__________。
该树的度为____________。
5
2
3
5
该树共有____________个节点、________条边。
13
12
在树形结构中,没有前驱的节点称为根节点(Root),
又称为开始节点。度为0的节点称为叶子节点(Leaf),它
又称为终端节点。树中度不为0的节点称为分支节点或者称
为非终端节点,除根节点外的分支节点统称为内部节点。
在上图中,节点A是根节点,节点G、H、C、D、K、L、M、
J、F都是叶子节点。
在树形结构中,对于两个以边直接连接的节点,上端节点
称为下端节点的父节点或双亲节点(Parent)。相应地,
下端节点称为上端节点的孩子节点(Child)。
A
B
G
H
C
D
E
F
I
J
K
L
M
节点K、L、M都是节点I的孩子节点
节点B是节点G、H的父节点
节点G、H是兄弟节点
树中节点的层数(Level)从根开始计算,根的层数为1,
其余节点的层数等于其父节点的层数加1。树中节点的最大
层数称为树的高度或深度(Depth)。
A
B
G
H
C
D
E
F
I
J
K
M
L
树的高度为4
节点G、H、I、J都在
第3层。
树形结构是比较复杂的非线性结构,在有多个节点
(节点个数>1)的树形结构中,它只有一个没有前驱、
只有后继的根节点,可以有多个没有后继、只有前驱的
叶子节点,其余的节点都只有一个直接前驱和多个直接后继。
二叉树
树的形态有很多,在实际的使用过程中,需要对树的形态
进一步地进行约束和简化,以便于设计和操作。二叉树是树形
结构的一个重要类型,在实际应用中,许多问题抽象出来的
数据结构往往就是二叉树的形式。
在猜数字游戏中,甲方事先在纸上写出一个100以内的正整
数,让乙方猜,乙方每猜一次,甲方都会告诉乙方“猜大了”
或是“猜小了”,直至猜出正确结果。
乙方如果采取“折半”的策略进行猜数字,就一定能
够在7次以内猜对结果,具体过程可以抽象成下图的二叉树结构。
50
25
12
37
6
18
31
43
75
62
56
68
88
82
96
小
小
小
小
小
小
小
大
大
大
大
大
大
大
二叉树的概念
二叉树(Binary Tree)是一个具有n(n>=0)个节点的有限
集合。当n=0时,二叉树是一棵空树;当n≠0时,则是一棵由
根节点和两棵互不相交的、分别称作这个根节点的左子树和右
子树组成的二叉树,由于左、右子树也是二叉树,因此子树也
可以是空树。
A
B
D
G
E
H
C
F
二叉树所有节点的度都小于或者等于2,
这给二叉树的操作带来了很大的方便。
一棵二叉树有5种可能的形态,如下图所示,从左到右
分别是:①空二叉树;②只有根节点的单点树;③只有
根节点和左子树;④只要根节点和右子树;⑤左右子树
均非空。
①
②
③
④
⑤
完全二叉树
这一类二叉树至多只有最下面两层中的节点度数小于2,
且最下面一层的叶子节点都依次排列在该层的最左边位置。
A
B
D
E
H
I
J
C
F
G
二叉树的性质
二叉树有很多性质,作为重要的数据结构,二叉树最重要
的性质就是树的高度和树中可以容纳的最大节点个数之间的
关系,主要有:
①二叉树的第k层上最多有2k-1(k>=1)个节点。
当k=1时,只有1(20=1)个根节点;当k=2时,由于节点的度
最大为2,因此,第2层的节点数最多有2(21=2)个节点。依次
推出,第k层上最多有2k-1个节点。
②深度为k的二叉树最多有2k-1(k>=1)个节点。
第1层至第k层上的最大节点数相加的结果是:20+21+…+2k-1=2k-1
因此2k-1是深度为k的二叉树的最多节点总数。
③在任意一棵二叉树中,若度为2的节点数量为n2,叶子节点(度为
0的节点)数为n0,则n0=n2+1。
假设度为0,1和2的节点数分别是n0,n1和n2,则二叉树中
总的节点数n=n0+n1+n2。
在二叉树的所有节点中,除了根节点没有前驱外,每个节点均有且
只有一个前驱节点,因此有n个节点的二叉树的总边数为n-1条。
根据度的定义,二叉树的总边数与度之间的关系:n-1=0*n0+1*n1+2*n2,
结合上述两个等式,可以得出n0=n2+1。
甲
乙
在甲树上,度为2的节点数是1,度为1的节点数是1,叶子节点数
为2;在乙树上,度为2的节点数是2,度为1的节点数是1,叶子
节点数为3。
二叉树在实际应用中非常广泛,如基于二叉树的查找方法
(二叉排序树查找),具有较高的查找效率,还能够在查找
表中进行数据插入和删除等动态查找操作。
最优二叉树(又称哈夫曼树,Huffman Tree)广泛应用于编码
和决策等方面。
练一练
1.一棵度为3,深度为4的树的节点个数至多为:
A.31
B.32
C.40
D.42
C
2.在一棵度为2的树中,度为2的节点数为15,度为1的节点数
为30,则叶子节点(度为0的节点)的个数为:
A.15
B.16
C.17
D.47
B
谢 谢
