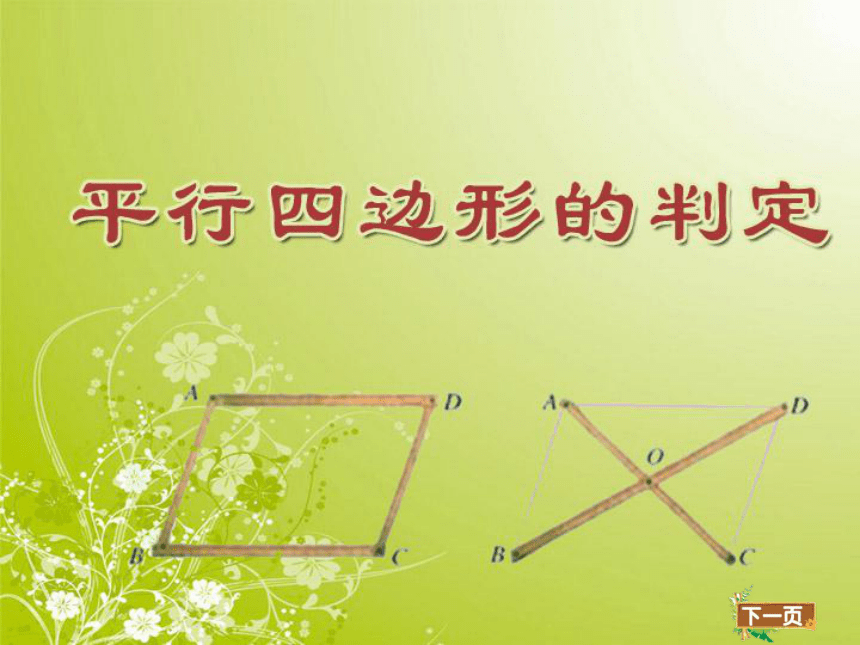
青岛版八年级数学下册课件6.2 平行四边形的判定(共22张PPT)
文档属性
| 名称 | 青岛版八年级数学下册课件6.2 平行四边形的判定(共22张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 23:31:21 | ||
图片预览



文档简介
(共22张PPT)
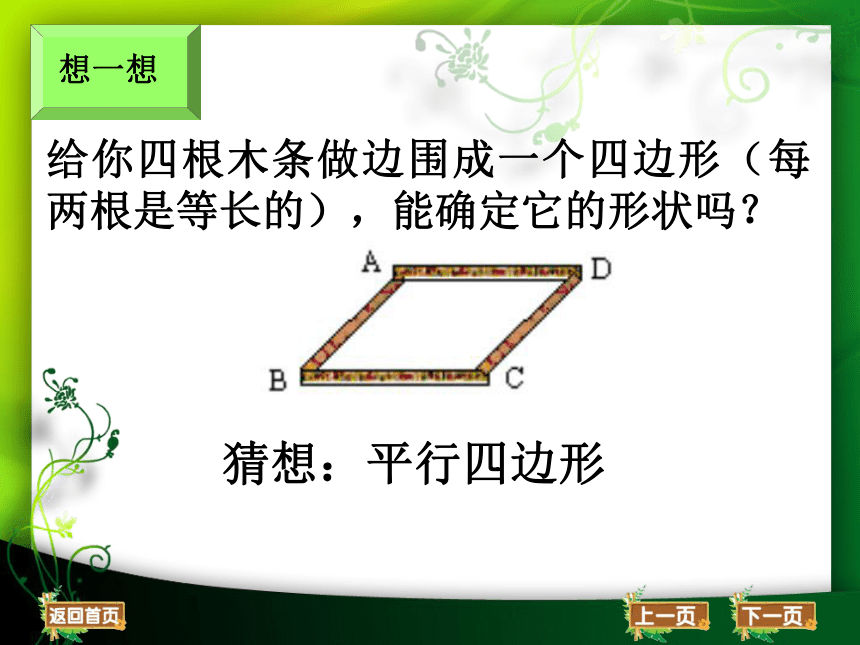
想一想
给你四根木条做边围成一个四边形(每两根是等长的),能确定它的形状吗?
猜想:平行四边形
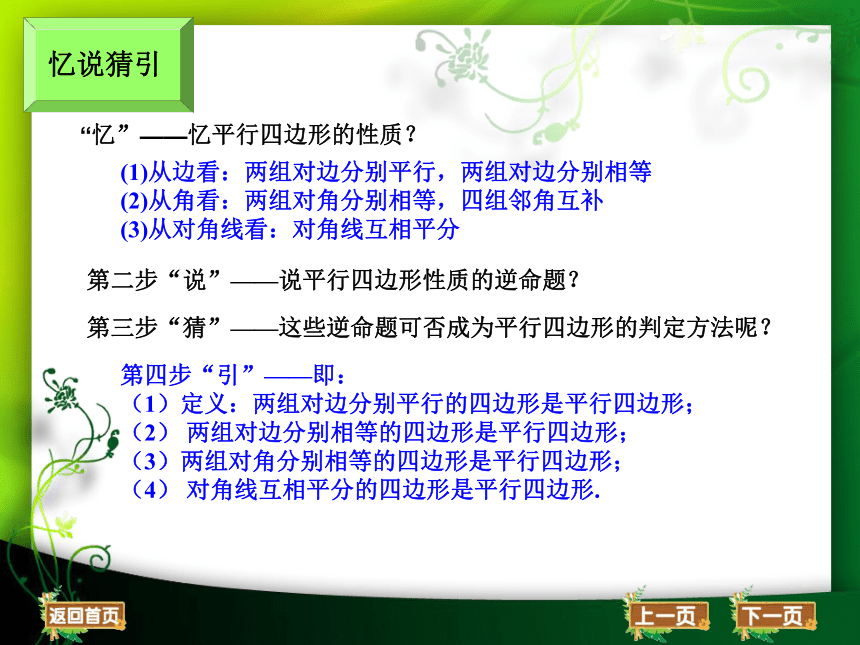
“忆”——忆平行四边形的性质?
忆说猜引
(1)从边看:两组对边分别平行,两组对边分别相等
(2)从角看:两组对角分别相等,四组邻角互补
(3)从对角线看:对角线互相平分
第二步“说”——说平行四边形性质的逆命题?
第三步“猜”——这些逆命题可否成为平行四边形的判定方法呢?
第四步“引”——即:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2) 两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4) 对角线互相平分的四边形是平行四边形.
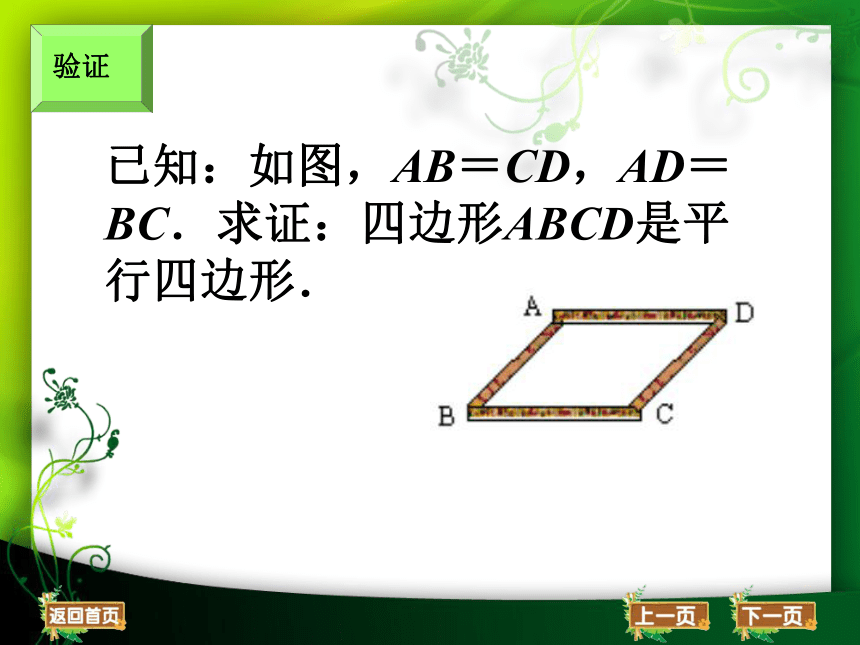
已知:如图,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
验证
两组对角分别相等的四边形是平行四边形吗?
思考
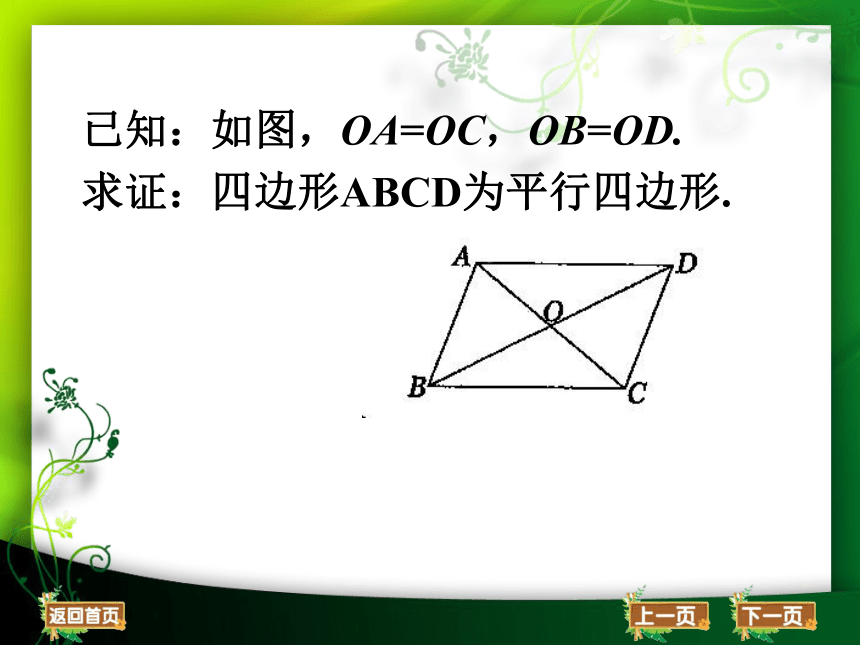
已知:如图,OA=OC,OB=OD.
求证:四边形ABCD为平行四边形.
练习
(2)
(1)
(3)
1.如图(1),若AD=8cm, AB=4cm,那么BC= cm, CD= cm时,四边形ABCD是平行四边形;
2.如图(2),AD=BC=16, AB=CD=15,CF=DE=9,图中有哪些互相平行的线段?
3.如图 (3),若AC=10cm, BD=8cm,则AO= cm, DO= cm时,则四边形ABCD为平行四边形.
【答案】:
(1)8、4
(2)AD∥BC、AB∥CD
(3)5、4
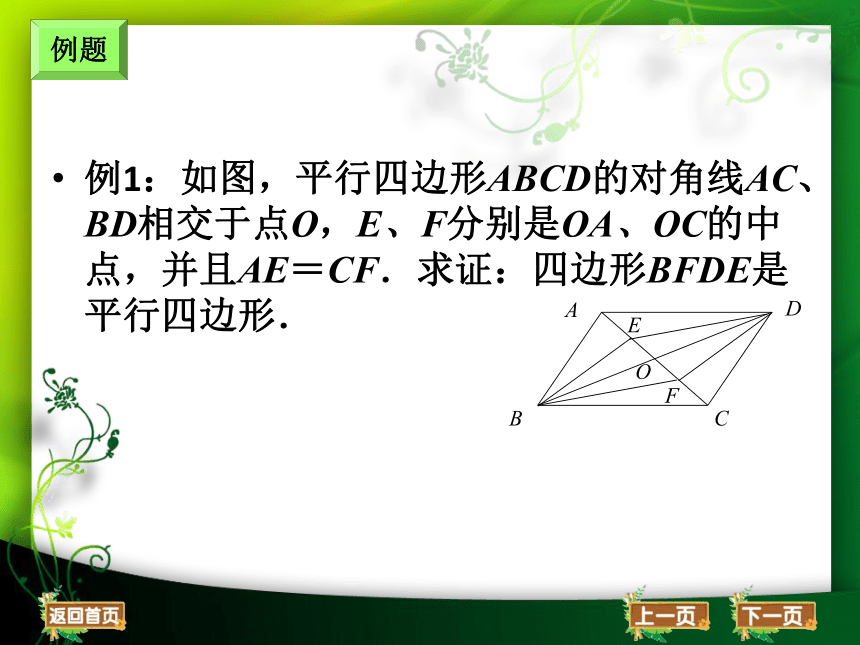
例1:如图,平行四边形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OC的中点,并且AE=CF.求证:四边形BFDE是平行四边形.
例题
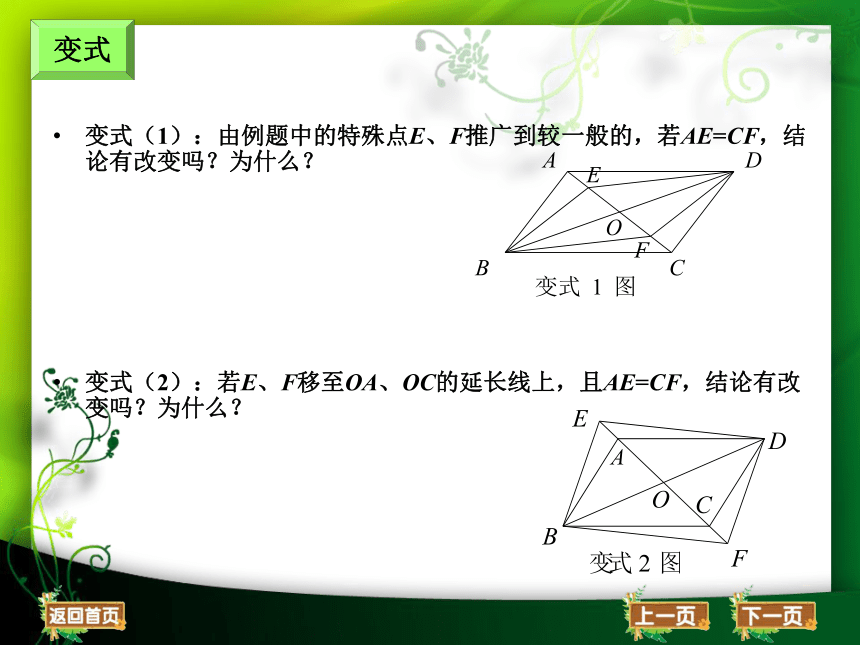
变式(1):由例题中的特殊点E、F推广到较一般的,若AE=CF,结论有改变吗?为什么?
变式(2):若E、F移至OA、OC的延长线上,且AE=CF,结论有改变吗?为什么?
变式
变式(3):若E、F、G、H分别为AO、CO、BO、DO的中点,四边形EGFH为平行四边形吗?
为什么?
变式(4):若变式(3)的条件成立,那么EF、GH有什么位置关系?
变式(5):在上题中,以图中的顶点为顶点,尽可能多地画出平行四边形。
变式
如图,在平行四边形ABCD中,已知AE、CF分别是∠BAD、 ∠BCD的角平分线,试说明四边形AFCE是平行四边形.
巩固题
取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
(即“一组对边平行且相等的四边形是平行四边形”吗?)
探究
C
B
A
D
1. 能判定一个四边形是平行四边形的条件是( ).
(A)一组对边平行,另一组对边相等 (B)一组对边平行,一组对角互补
(C)一组对角相等,一组邻角互补 (D)一组对角相等,另一组对角互补
2. □ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为( ).
A (1,-2) B (2,-1) C (1,-3) D (2,-3)
3. 如图,在□ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.
练习
答案:1.C 2.A 3.思路1:根据一组对边平行且相等的四边形是平行四边形得四边形AECF、BEDF是平行四边形,再根据定义判定四边形EGFH是平行四边形.
4. 已知:如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.求证:CF∥AE.
练习
证明:∵AF∥BE,∴∠FAC=∠ECA
∵D是AC的中点∴AD=CD∴△AFD≌△CED
∴AF=CE∴四边形AFCE是平行四边形
问题一:1.将任意一个三角形分成四个面积相等的的三角形,你是如何切割的?
思考
B
A
C
B
A
C
2.连接任意两边中点的线段与第三边之间有怎样的位置和大小关系?
已知:△ABC中,D、E分别是AB、AC的中点.
求证:DE∥BC,DE= BC.
问题2:如图,a,b是两条平行线,从直线a上的任意一点A向直线b作垂线l,垂足为点B,我们得到线段AB.按同样的作法,我们作出线段CD.你能发现AB与CD的关系吗?
思考
1. 如图△ABC的边AB=12,BC=10,AC=8,点D,E,F分别是△ABC的三边的中点.
⑴求连结各边中点所成的三角形的周长;
⑵以这些点为顶点,你能在图中画出多少个平行四边形.
2. 如图,点D,E分别是△ABC的边AB,
AC的中点,AF是BC边上的中线,
⑴若EF=5cm,则AB= cm;
若BC=9cm,则DE= cm.
⑵中线AF与中位线DE有什么特殊
关系?证明你的结论.
例题
1.在△ABC中,D、E、F是三边的中点,AB=7,BC=6,AC=10,则四边形DBEF的周长为 .
2.已知△ABC中的周长为50cm,D、E、F分别为△ABC中AB、BC、AC边上的中点,且DE=8cm,EF=10cm,则DF的长为 cm.
3.已知第一个三角形的周长为a,它的三条中位线组成第二个三角形,其周长为 ;第二个三角形的三条中位线又组成第三个三角形,其周长为 ;以此类推,第2009个三角形的周长为 .
练习
4.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.求证:EF∥BC.
练习
5.如图,在四边形ABCD中,E、F、G、H分别AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
练习
你有哪些收获呢?
小结
知识:
1. 判别方法:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2) 两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4) 对角线互相平分的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形.
2. 三角形的中位线:三角形的中位线平行于第三边且等于第三边的一半.
思想方法:类比、化归、探究法.
想一想
给你四根木条做边围成一个四边形(每两根是等长的),能确定它的形状吗?
猜想:平行四边形
“忆”——忆平行四边形的性质?
忆说猜引
(1)从边看:两组对边分别平行,两组对边分别相等
(2)从角看:两组对角分别相等,四组邻角互补
(3)从对角线看:对角线互相平分
第二步“说”——说平行四边形性质的逆命题?
第三步“猜”——这些逆命题可否成为平行四边形的判定方法呢?
第四步“引”——即:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2) 两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4) 对角线互相平分的四边形是平行四边形.
已知:如图,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
验证
两组对角分别相等的四边形是平行四边形吗?
思考
已知:如图,OA=OC,OB=OD.
求证:四边形ABCD为平行四边形.
练习
(2)
(1)
(3)
1.如图(1),若AD=8cm, AB=4cm,那么BC= cm, CD= cm时,四边形ABCD是平行四边形;
2.如图(2),AD=BC=16, AB=CD=15,CF=DE=9,图中有哪些互相平行的线段?
3.如图 (3),若AC=10cm, BD=8cm,则AO= cm, DO= cm时,则四边形ABCD为平行四边形.
【答案】:
(1)8、4
(2)AD∥BC、AB∥CD
(3)5、4
例1:如图,平行四边形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OC的中点,并且AE=CF.求证:四边形BFDE是平行四边形.
例题
变式(1):由例题中的特殊点E、F推广到较一般的,若AE=CF,结论有改变吗?为什么?
变式(2):若E、F移至OA、OC的延长线上,且AE=CF,结论有改变吗?为什么?
变式
变式(3):若E、F、G、H分别为AO、CO、BO、DO的中点,四边形EGFH为平行四边形吗?
为什么?
变式(4):若变式(3)的条件成立,那么EF、GH有什么位置关系?
变式(5):在上题中,以图中的顶点为顶点,尽可能多地画出平行四边形。
变式
如图,在平行四边形ABCD中,已知AE、CF分别是∠BAD、 ∠BCD的角平分线,试说明四边形AFCE是平行四边形.
巩固题
取两根等长的木条AB、CD,将它们平行放置,再用两根木条BC、AD加固,得到的四边形ABCD是平行四边形吗?
(即“一组对边平行且相等的四边形是平行四边形”吗?)
探究
C
B
A
D
1. 能判定一个四边形是平行四边形的条件是( ).
(A)一组对边平行,另一组对边相等 (B)一组对边平行,一组对角互补
(C)一组对角相等,一组邻角互补 (D)一组对角相等,另一组对角互补
2. □ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为( ).
A (1,-2) B (2,-1) C (1,-3) D (2,-3)
3. 如图,在□ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.
练习
答案:1.C 2.A 3.思路1:根据一组对边平行且相等的四边形是平行四边形得四边形AECF、BEDF是平行四边形,再根据定义判定四边形EGFH是平行四边形.
4. 已知:如图,△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.求证:CF∥AE.
练习
证明:∵AF∥BE,∴∠FAC=∠ECA
∵D是AC的中点∴AD=CD∴△AFD≌△CED
∴AF=CE∴四边形AFCE是平行四边形
问题一:1.将任意一个三角形分成四个面积相等的的三角形,你是如何切割的?
思考
B
A
C
B
A
C
2.连接任意两边中点的线段与第三边之间有怎样的位置和大小关系?
已知:△ABC中,D、E分别是AB、AC的中点.
求证:DE∥BC,DE= BC.
问题2:如图,a,b是两条平行线,从直线a上的任意一点A向直线b作垂线l,垂足为点B,我们得到线段AB.按同样的作法,我们作出线段CD.你能发现AB与CD的关系吗?
思考
1. 如图△ABC的边AB=12,BC=10,AC=8,点D,E,F分别是△ABC的三边的中点.
⑴求连结各边中点所成的三角形的周长;
⑵以这些点为顶点,你能在图中画出多少个平行四边形.
2. 如图,点D,E分别是△ABC的边AB,
AC的中点,AF是BC边上的中线,
⑴若EF=5cm,则AB= cm;
若BC=9cm,则DE= cm.
⑵中线AF与中位线DE有什么特殊
关系?证明你的结论.
例题
1.在△ABC中,D、E、F是三边的中点,AB=7,BC=6,AC=10,则四边形DBEF的周长为 .
2.已知△ABC中的周长为50cm,D、E、F分别为△ABC中AB、BC、AC边上的中点,且DE=8cm,EF=10cm,则DF的长为 cm.
3.已知第一个三角形的周长为a,它的三条中位线组成第二个三角形,其周长为 ;第二个三角形的三条中位线又组成第三个三角形,其周长为 ;以此类推,第2009个三角形的周长为 .
练习
4.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.求证:EF∥BC.
练习
5.如图,在四边形ABCD中,E、F、G、H分别AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
练习
你有哪些收获呢?
小结
知识:
1. 判别方法:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2) 两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4) 对角线互相平分的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形.
2. 三角形的中位线:三角形的中位线平行于第三边且等于第三边的一半.
思想方法:类比、化归、探究法.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
