【课件】7.3 离散型随机变量的数字特征-7.3.2 离散型随机变量的方差 数学-RJA-选择性必修第三册 (共27张PPT)
文档属性
| 名称 | 【课件】7.3 离散型随机变量的数字特征-7.3.2 离散型随机变量的方差 数学-RJA-选择性必修第三册 (共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 09:47:49 | ||
图片预览








文档简介
(共27张PPT)
数学-RJ·A-选择性必修第三册
7.3 离散型随机变量的数字特征
7.3.2 离散型随机变量的方差
第七章 随机变量及其分布
学习目标
1.通过具体实例,理解取有限值的离散型随机变量的方差与标准差的概念.
2.能计算简单离散型随机变量的方差,并能解决一些实际问题.
3.掌握方差的性质以及两点分布的方差的求法.
重点:离散型随机变量的方差的含义.
难点:利用离散型随机变量的方差解决实际问题.
知识梳理
一、离散型随机变量的方差及其计算公式
设离散型随机变量X的分布列如下表所示.
X x1 x2 … xn
P p1 p2 … pn
考虑X所有可能取值xi与E(X)的偏差的平方(x1-E(X))2,(x2-E(X))2,
…,(xn-E(X))2.因为X取每个值的概率不尽相同,所以我们用偏差平方关于
取值概率的加权平均,来度量随机变量X取值与其均值E(X)的偏离程度.
我们称
为随机变量X的方差,有时也记为Var(X),
并称为随机变量X的标准差,记为σ(X).
对随机变量X的方差、标准差的理解
(1)随机变量X的方差和标准差都反映了随机变量X取值的稳定性以及波动、集中与离散程度.
(2)D(X)越小,随机变量X取值的稳定性越高,波动越小.
(3)方差的单位是随机变量单位的平方,而标准差与随机变量本身有相同的单位,所以在实际问题中应用更广泛.
在方差的计算中,利用下面的结论经常可以使计算简化.
二、方差的性质
离散型随机变量X加上一个常数b,仅仅使X的值产生一个平移,不改变X与其均值的离散程度,方差保持不变,
即D(X+b)=D(X).
而离散型随机变量X乘以一个常数a,其方差变为原方差的a2倍,即D(aX)=a2D(X).
一般地,可以证明下面的结论成立:
D(aX+b)=a2D(X).
常考题型
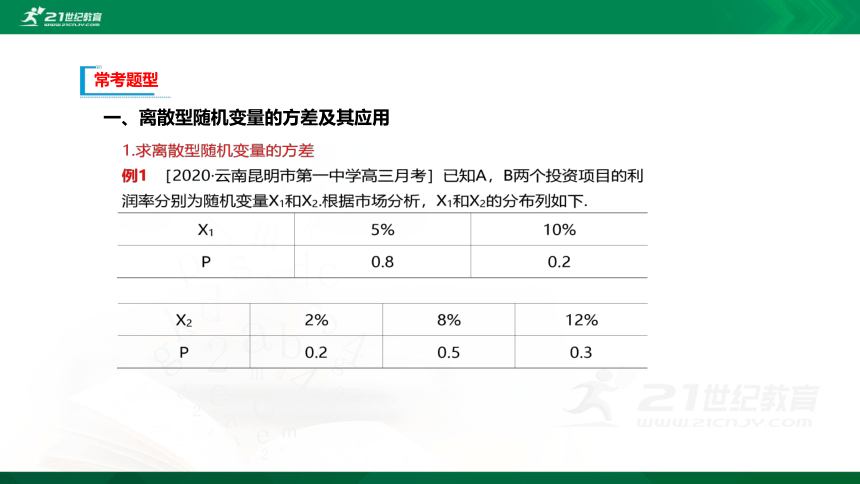
一、离散型随机变量的方差及其应用
(1)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求D(Y1)和D(Y2).
(2)将x(0≤x≤100)万元投资A项目,(100-x)万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差之和,求f(x)的最小值,并指出当x为何值时,f(x)取得最小值.
【解】(1)E(Y1)=5%×100×0.8+10%×100×0.2=6,
D(Y1)=(5%×100-6)2×0.8+(10%×100-6)2×0.2=4;
E(Y2)=2%×100×0.2+8%×100×0.5+12%×100×0.3=8,
D(Y2)=(2%×100-8)2×0.2+(8%×100-8)2×0.5+(12%×100-8)2 ×0.3 =12.
◆求离散型随机变量方差的步骤
1.明确随机变量的可能取值及每一个值的试验结果;
2.求出随机变量各取值对应的概率;
3.写出随机变量的分布列;
4.求出随机变量的均值;
5.代入随机变量方差的公式求出方差.
C
◆已知方差求参数的方法
1.根据题目条件中给出的分布列,可以列出参数之间的关系.
2.根据期望和方差的值可以得到参数的关系.
3.联立可得关于参数的方程(组).
4.解方程(组)即可求得参数值.
A
D
二、方差的性质及应用
训练题
1.[2020·广东中山高二期末]已知X是离散型随机变量,P(X=1)=,P(X=a)=,E(X)=,则D(2X-1)= ( )
A. B. C. D.
2.[2020·山西长治二中高二期中]若随机变量ξ满足E(1-ξ)=4,D(1-ξ)=4,则下列说法正确的是 ( )
A.E(ξ)=-4,D(ξ)=4 B.E(ξ)=-3,D(ξ)=3
C.E(ξ)=-4,D(ξ)=-4 D.E(ξ)=-3,D(ξ)=4
B
D
三、两点分布的方差
【解析】D(X)=(1-p)p=,整理得p2-p=0.
又0【答案】C
C
A
四、方差在决策问题中的应用
例5 [2020·广东揭阳高二期末]某投资公司对以下两个项目进行前期市场调研.项目A:通信设备.根据调研,投资到该项目上,所有可能结果为获利40%、亏损20%、不赔不赚,且这三种情况发生的概率分别为,,a.
项目B:新能源汽车.根据调研,投资到该项目上,所有可能结果为获利30%、亏损10%,且这两种情况发生的概率分别为b,c.
经测算,当投入A,B两个项目的资金相等时,它们所获得的平均收益(即数学期望)也相等.
(1)求a,b,c的值;
(2) 若将100万元全部投到其中的一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
◆方差在决策问题中的应用
在一些决策问题中,均值仅体现了随机变量取值的平均水平,方差说明随机变量取值的离散程度,因此,利用均值和方差的意义可以分析、解决实际问题.
训练题 [2020·河北安平中学高二期中]设甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数均大于6,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的数学期望与方差,并以此比较甲、乙的射击技术.
解:(1)由题意得0.5+3a+a+0.1=1,
解得a=0.1.
因为乙射中10,9,8环的概率分别为0.3,0.3,0.2,
所以乙射中7环的概率为1-(0.3+0.3+0.2)=0.2.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-选择性必修第三册
7.3 离散型随机变量的数字特征
7.3.2 离散型随机变量的方差
第七章 随机变量及其分布
学习目标
1.通过具体实例,理解取有限值的离散型随机变量的方差与标准差的概念.
2.能计算简单离散型随机变量的方差,并能解决一些实际问题.
3.掌握方差的性质以及两点分布的方差的求法.
重点:离散型随机变量的方差的含义.
难点:利用离散型随机变量的方差解决实际问题.
知识梳理
一、离散型随机变量的方差及其计算公式
设离散型随机变量X的分布列如下表所示.
X x1 x2 … xn
P p1 p2 … pn
考虑X所有可能取值xi与E(X)的偏差的平方(x1-E(X))2,(x2-E(X))2,
…,(xn-E(X))2.因为X取每个值的概率不尽相同,所以我们用偏差平方关于
取值概率的加权平均,来度量随机变量X取值与其均值E(X)的偏离程度.
我们称
为随机变量X的方差,有时也记为Var(X),
并称为随机变量X的标准差,记为σ(X).
对随机变量X的方差、标准差的理解
(1)随机变量X的方差和标准差都反映了随机变量X取值的稳定性以及波动、集中与离散程度.
(2)D(X)越小,随机变量X取值的稳定性越高,波动越小.
(3)方差的单位是随机变量单位的平方,而标准差与随机变量本身有相同的单位,所以在实际问题中应用更广泛.
在方差的计算中,利用下面的结论经常可以使计算简化.
二、方差的性质
离散型随机变量X加上一个常数b,仅仅使X的值产生一个平移,不改变X与其均值的离散程度,方差保持不变,
即D(X+b)=D(X).
而离散型随机变量X乘以一个常数a,其方差变为原方差的a2倍,即D(aX)=a2D(X).
一般地,可以证明下面的结论成立:
D(aX+b)=a2D(X).
常考题型
一、离散型随机变量的方差及其应用
(1)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求D(Y1)和D(Y2).
(2)将x(0≤x≤100)万元投资A项目,(100-x)万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差之和,求f(x)的最小值,并指出当x为何值时,f(x)取得最小值.
【解】(1)E(Y1)=5%×100×0.8+10%×100×0.2=6,
D(Y1)=(5%×100-6)2×0.8+(10%×100-6)2×0.2=4;
E(Y2)=2%×100×0.2+8%×100×0.5+12%×100×0.3=8,
D(Y2)=(2%×100-8)2×0.2+(8%×100-8)2×0.5+(12%×100-8)2 ×0.3 =12.
◆求离散型随机变量方差的步骤
1.明确随机变量的可能取值及每一个值的试验结果;
2.求出随机变量各取值对应的概率;
3.写出随机变量的分布列;
4.求出随机变量的均值;
5.代入随机变量方差的公式求出方差.
C
◆已知方差求参数的方法
1.根据题目条件中给出的分布列,可以列出参数之间的关系.
2.根据期望和方差的值可以得到参数的关系.
3.联立可得关于参数的方程(组).
4.解方程(组)即可求得参数值.
A
D
二、方差的性质及应用
训练题
1.[2020·广东中山高二期末]已知X是离散型随机变量,P(X=1)=,P(X=a)=,E(X)=,则D(2X-1)= ( )
A. B. C. D.
2.[2020·山西长治二中高二期中]若随机变量ξ满足E(1-ξ)=4,D(1-ξ)=4,则下列说法正确的是 ( )
A.E(ξ)=-4,D(ξ)=4 B.E(ξ)=-3,D(ξ)=3
C.E(ξ)=-4,D(ξ)=-4 D.E(ξ)=-3,D(ξ)=4
B
D
三、两点分布的方差
【解析】D(X)=(1-p)p=,整理得p2-p=0.
又0
C
A
四、方差在决策问题中的应用
例5 [2020·广东揭阳高二期末]某投资公司对以下两个项目进行前期市场调研.项目A:通信设备.根据调研,投资到该项目上,所有可能结果为获利40%、亏损20%、不赔不赚,且这三种情况发生的概率分别为,,a.
项目B:新能源汽车.根据调研,投资到该项目上,所有可能结果为获利30%、亏损10%,且这两种情况发生的概率分别为b,c.
经测算,当投入A,B两个项目的资金相等时,它们所获得的平均收益(即数学期望)也相等.
(1)求a,b,c的值;
(2) 若将100万元全部投到其中的一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合理的项目,并说明理由.
◆方差在决策问题中的应用
在一些决策问题中,均值仅体现了随机变量取值的平均水平,方差说明随机变量取值的离散程度,因此,利用均值和方差的意义可以分析、解决实际问题.
训练题 [2020·河北安平中学高二期中]设甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数均大于6,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的数学期望与方差,并以此比较甲、乙的射击技术.
解:(1)由题意得0.5+3a+a+0.1=1,
解得a=0.1.
因为乙射中10,9,8环的概率分别为0.3,0.3,0.2,
所以乙射中7环的概率为1-(0.3+0.3+0.2)=0.2.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
