2021-2022学年高二下学期数学人教A版(2019)必修第三册6.1分类加法计数原理与分步乘法计数原理课件(32张ppt)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)必修第三册6.1分类加法计数原理与分步乘法计数原理课件(32张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 641.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 09:37:06 | ||
图片预览











文档简介
(共32张PPT)
6.1 分类加法计数原理与分步乘法计数原理
第六章 计数原理
汽车号牌的序号一般是从26个英文字母、10 个阿拉伯数字中选出若干个,并按适当顺序排列而成. 随着人们生活水平的提高,家庭汽车拥有量迅速增长,汽车号牌序号需要扩容. 那么,交通管理部门应如何确定序号的组成方法,才能满足民众的需求呢 这就需要“数(shu)出”某种汽车号牌序号的组成方案下所有可能的序号数,这就是计数.
日常生活、生产中类似的问题大量存在. 例如,幼儿会通过一个一个地数的方法,统计自己拥有玩具的数量;学校要举行班际篮球比赛,在确定赛制后,体育组的老师需要知道共需要举行多少场比赛;用红、黄、绿三面旗帜组成航海信号,颜色的不同排列表示不同的信号,需要知道共可以组成多少种不同的信号 如果问题中数量很少,一个一个地数也不失为一种计数的好方法. 但如果问题中数量很多,我们还一个一个地去数吗
在小学我们学了加法和乘法,这是将若干个“小”的数结合成“较大”的数最基本的方法. 这两种方法经过推广就成了本章将要学习的分类加法计数原理和分步乘法计数原理. 这两个原理是解决计数问题的最基本、最重要的方法,利用两个计数原理还可以得到两类特殊计数问题的计数公式—排列数公式和组合数公式,应用公式就可以方便地解决一些计数问题. 作为计数原理与计数公式的一个应用,本章我们还将学习在数学上有广泛应用的二项式定理.
计数问题是我们从小就经常遇到的,通过列举一个一个地数是计数的基本方法. 但当问题中的数量很大时,列举的方法效率不高. 能否设计巧妙的“数法”,以提高效率呢 下面先分析一个简单的问题,并尝试从中得出巧妙的计数方法.
思考 用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码
因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+ 10=36种不同的号码.
探究 你能说一说这个问题的特征吗
首先,这里要完成的事情是“给一个座位编号”;其次是“或”字的出现: 一个座位编号用一个英文字母或一个阿拉伯数字表示. 因为英文字母与阿拉伯数字互不相同,所以用英文字母编出的号码与用阿拉伯数字编出的号码也互不相同.这两类号码数相加就得到号码的总数.
这里的“或”代表分类.
上述计数过程的基本环节是:
(1) 确定分类标准,根据问题条件分为字母号码和数字号码两类;
(2) 分别计算各类号码的个数;
(3) 各类号码的个数相加,得出所有号码的个数.
我们把这种计数方法称为分类加法计数原理.
一般地,如果完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有
N=m+n
种不同的方法.
分类加法计数原理:
两类不同方案中的方法互不相同
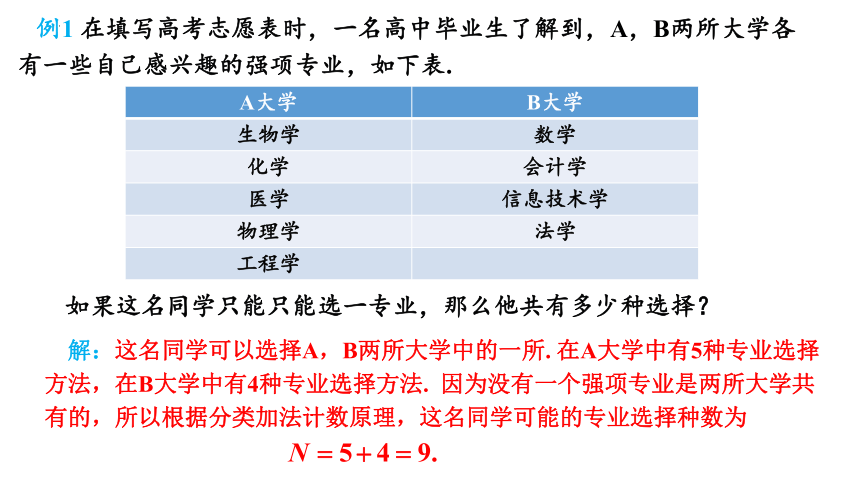
例1 在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,如下表.
如果这名同学只能只能选一专业,那么他共有多少种选择?
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
解:这名同学可以选择A,B两所大学中的一所. 在A大学中有5种专业选择方法,在B大学中有4种专业选择方法. 因为没有一个强项专业是两所大学共有的,所以根据分类加法计数原理,这名同学可能的专业选择种数为
2. 在例1中,如果数学也是A大学的强项专业,那么A大学共有6个专业可以选择,B大学共有4个专业可以选择,应用分类加法计数原理,得到这名同学可能的专业选择种数为6+4=10. 这种算法有什么问题?
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
数学
解:这种算法有问题,因为问题强调的是这名同学的专业选择,故并不需要考虑学校的差异,所以这名同学可能的专业选择种数应当为
课本P5
特别地,如果完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法, 在第n类方案中有mn种不同的方法,那么完成这件事共有m1+m2+ +mn种不同的方法.
探究 如果完成一件事有三类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,在第3类方案中有m3种不同的方法,那么完成这件事共有多少种不同的方法
如果完成一件事有n类不同方案,在每一类方案中都有若干种不同的方法,那么应当如何计数呢
根据分类加法计数原理,可知完成这件事共有m1+m2+m3种不同的方法.
各类不同方案中的方法互不相同
正确理解分类(加法)计数原理:
① 分类加法计数原理针对的是“分类”问题,
② 完成一件事要分为若干类,
③ 各类的方法相互独立,
④ 各类中的各种方法也相对独立,
⑤ 用任何一类中的任何一种方法都可以单独完成这件事.
思考 用前6个大写英文字母和1~9这9个阿拉伯数字,以A1, A2, , A9, B1, B2, 的方式给教室里的一个座位编号,总共能编出多少种不同的号码
这里要完成的事情仍然是“给一个座位编号”,但与前一问题的要求不同.在前一问题中,用26个英文字母中的任意一个或10个阿拉伯数字中的任意一个,都可以给出一个座位号码. 但在这个问题中,号码必须由一个英文字母和一个作为下标的阿拉伯数字组成,即得到一个号码要经过先确定一个英文字母,后确定一个阿拉伯数字这样两个步骤. 用右图所示的方法可以列出所有可能的号码.
A
1
9
4
2
3
数字
5
7
6
8
字母
得到的号码
A1
A2
A3
A4
A5
A6
A7
A8
A9
树状图
能用树状图列出所有可能的号码吗?
由此可得,能编出的不同号码共有
上述问题要完成的一件事情仍然是“给 一个座位编号”,其中最重要的特征是“和”字的出现:一个座位编号由一个英文字母和一个阿拉伯数字构成. 因此得到一个座位号要经过先确定一个英文字母, 后确定一个阿拉伯数字这两个步骤,每一个英文字母与不同的数字组成的号码是互不相同的.
我们把上述这种计数方法称为分步乘法计数原理.
分步乘法计数原理:
一般地,完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有
N=m×n
种不同的方法.
注意:无论第1步采用哪种方法,与之对应的第2步都有相同的方法数.
特别地,如果完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法, ,做第n步有mn种不同的方法,那么完成这件事共有 种不同的方法.
正确理解分步乘法计数原理:
① 分步计数原理针对的是“分步”问题,
② 完成一件事要分为若干步,
③ 各个步骤相互依存,
④ 完成任何其中的一步都不能完成该件事,
⑤ 只有当各个步骤都完成后,才算完成这件事.
例2 某班有男生30名、女生24名,从中任选男生和女生各1名代表班级参加比赛,共有多少种不同的选法
解:第1步,从30名男生中选出1人,有30种不同选法;
第2步,从24名女生中选出1人,有24种不同选法.
根据分步乘法计数原理,共有不同选法的种数为
N=30×24= 720.
例3 书架的第 1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1) 从书架上任取1本书,有多少种不同取法
(2) 从书架的第1层、第2层、第3层各取1本书,有多少种不同取法
解:(1) 根据分类加法计数原理,不同的取法种数为
N=4+3+2=9.
(2) 根据分步乘法计数原理,不同的取法种数为
N=4×3×2= 24.
1. 填空题
(1) 一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这项工作,不同选法的种数是________;
(2) 从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同路线的条数是_________.
9
6
课本P5
3. 书架上层放有6本不同的数学书,下层放有5本不同的语文书.
(1) 从书架上任取1本书,有多少种不同的取法
(2) 从书架上任取数学书和语文书各1本,有多少种不同的取法
4. 现有高一年级的学生3名,高二年级的学生5名,高三年级的学生4名.
(1) 从三个年级的学生中任选1人参加接待外宾的活动,有多少种不同的选法
(2) 从三个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法
解:(1) 11种;(2) 30种.
解:(1) 12种;(2) 60种.
课本P6
解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第1步,从3幅画中选1幅挂在左边墙上,有3种选法;
第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法.
根据分步乘法计数原理,不同挂法的种数为
N=3×2=6.
这6种挂法如右图所示.
例4 要从甲、 乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法 .
乙
乙
丙
甲
右边
丙
乙
甲
左边
得到的挂法
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
甲
丙
分类加法计数原理和分步乘法计数原理,回答的都是有关做一件事的不同方法种数的问题. 区别在于:
分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事,关键词是“分类”;
分步乘法计数原理针对的是“分步”问题,各个步骤中的方法互相依存,只有每一个步骤都完成才算做完这件事,关键词是“分步”.
例5 给程序模块命名,需要用3个字符,其中首字符要求用字母A~G或U~Z,后两个要求用数字1 ~9,最多可以给多少个程序命名?
解2: 首字符用A~G给程序命名的个数为 7×9×9=567.
首字符用U~Z给程序命名的个数为 6×9×9=486.
∴总的不同名称的个数是 567+486=1053.
思考 你还能给出不同的解法吗
解: 由分类加法计数原理,首字符不同选法的种数为
7+6=13.
后两个字符从1~9中选,因为数字可以重复,所以不同选法的种数都为9.
由分步乘法计数原理,不同名称的个数是
13×9×9=1053,
即最多可以给1053个程序模块命名.
例6 电子元件很容易实现电路的通与断、电位的高与低等两种状态,而这也是最容易控制的两种状态. 因此计算机内部就采用了每一位只有0或1两种数字的记数法,即二进制. 为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用1个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成.
(1) 1个字节(8位)最多可以表示多少个不同的字符
(2) 计算机汉字国标码包含了6763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示
解: (1) 由分步乘法计数原理,1个字节最多可以表示不同的字符个数是
2×2×2×2×2×2×2×2=28=256.
(2) 由(1)知,1个字节最多可以表示256个不同的字符,则2个字节最多就可以表示256 ×256=65536>6763,所以每个汉字至少要用2个字节表示.
1. 某电话局管辖范围内的电话号码由8位数字组成,其中前4位的数字是不变的,后4位数字都是0~9中的一个数字,这个电话局不同的电话号码最多有多少个
解:104=10000 (个).
2. 从5名同学中选出正、副组长各1名,有多少种不同的选法
解:5×4=20 (种).
3. 从1, 2, , 19, 20中任选一个数作被减数,再从1, 2, , 10中任选一个数作减数,然后写成一个减法算式,共可得到多少个不同的算式
解:20×10=200 (个).
课本P7
解1:被5除余2的正整数的个位是2或7.
当满足条件的数是一位数时,满足条件的个数有2个 ;
当满足条件的数是两位数时,满足条件的个数有9×2=18个 ;
当满足条件的数是三位数时,满足条件的个数有4×10×2= 80个 .
所以满足条件的数共有100个.
4. 在1, 2, , 500中,被5除余2的数共有多少个
解2:被5除余2的数可以表示为5k+2 (k为整数).
由1≤5k+2≤500,解得0≤k≤99,
满足条件的k值有100个, 所以满足条件的数共有100个.
解:满足条件的三位数有5×5×5= 125 个 .
5. 由数字1, 2, 3, 4, 5可以组成多少个三位数(各位上的数字可以重复)
课本P7
例7 计算机编程人员在编写好程序以后需要对程序进行测试. 程序员需要知道到底有多少条执行路径(程序从开始到结束的路线),以便知道需要提供多少个测试数据. 一般地,一个程序模块由许多子模块组成. 下图是一个具有许多执行路径的程序模块,它有多少条执行路径
另外,为了减少测试时间,程序员需要设法减少测试次数. 你能帮助程序员设计一个测试方法,以减少测试次数吗
解:由程序模块可得,执行路径条数有
(18+45+28)×(38+43)=7371.
为了减少测试次数,可单独测试5个模块和模块1,2,3与模块4,5之间的信息交流是否正常即可,这样测试的次数只有
(18+45+28 +38 +43)×(3×2)=178 (次).
例8 通常, 我国民用汽车号牌的编号由两部分组成: 第一部分为用汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.
其中,序号的编码规则为:
(1) 由10个阿拉伯数字和除O,I之外的24个英文字母组成;
(2) 最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,那
么这个发牌机关最多能发放多少张汽车号牌
解:当序号中没有字母时,号牌张数为 105=100000.
当序号中有1位字母时,号牌张数为5×24×104=1200000.
当序号中有2位字母时,号牌张数为10×242×103=5760000.
所以这个发牌机关最多能发的汽车号牌张数为7060000.
归纳:
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析两点:
(1) 要完成的“一件事”是什么;
(2) 需要分类还是需要分步.
分类要做到“不重不漏”. 分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务. 分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
解:展开后共有3×3×5=45项.
1. 乘积(a1+a2+a3)(b1+b2+b3)(c1+c2+c3+c4+c5) 展开后共有多少项
解:9+8+7+6+5+4+3+2+1=45 (个).
2. 在所有的两位数中,个位数字小于十位数字的有多少个
3. 某商场有6个门,如果某人从其中的任意一个门进人商场,并且要求从其他的门出去,那么共有多少种不同的进出商场的方式
解:进出商场的不同方式有6×5=30(种).
4.任意画一条直线,在直线上任取n个分点.
(1) 从这n个分点中任取2个点形成一条线段,可得到多少条线段
(2) 从这n个分点中任取2个点形成一个向量,可得到多少个向量
解:
课本P11
练习2 运动会有跳高、跑步、游泳三个比赛项目,某班有四名同学报名参赛,要求每名同学只能参加一个项目,不同的报名方式共有( )
A. 4种 B. 24种 C. 43种 D. 34种
练习1 四名同学,争夺三项冠军(每项没有并列冠军),则冠军获得者可能有的种类是( )
A. 4 B. 24 C. 43 D. 34
C
D
练习3 现有高一学生9人,高二学生12人,高三学生7人,自发组织数学课外活动小组,从中推选两名来自不同年级的学生做一次活动的主持人,有_____种不同选法.
解:
推选两名来自不同年级的学生做一次活动主持人,有不同选法:
9×12 +12×7 +9×7
= 255(种).
练习4 长方形的两条对角线把长方形分成四部分,如图用五种不同的颜色给这四部分涂色,每一部分涂一种颜色,任何相邻(具有公共边)的两部分涂不同颜色,问有多少种不同的涂色方法?
A
B
C
D
解1:
若A, C同色,则不同的涂色方法有
5×4×4=80 (种).
(2) 若A, C不同色,则不同的涂色方法有
5×4×3×3=180 (种).
综上所述,由分类计数原理得:
共有80+180=260 (种).
练习4 长方形的两条对角线把长方形分成四部分,如图用五种不同的颜色给这四部分涂色,每一部分涂一种颜色,任何相邻(具有公共边)的两部分涂不同颜色,问有多少种不同的涂色方法?
A
B
C
D
解2:
由题意四部分最多涂4种颜色,最少涂2种颜色,
若涂4种颜色,则不同的涂色方法有
5×4×3×2=120 (种).
(2) 若涂3种颜色,则不同的涂色方法有
5×4×3×2=120 (种).
(3) 若涂2种颜色,则不同的涂色方法有
5×4=20 (种).
综上所述,由分类计数原理得:
共有120+120+20=260 (种).
解1:
变式 将一个四棱锥的每个顶点染上一种颜色,使同一条棱的两端点异色,如果只有五种颜色可供使用,那么不同的染色方法总数是多少?
S
A
B
C
D
若A, C同色,则不同的染色方法有
5×4×3×3=180 (种).
(2) 若A, C不同色,则不同的染色方法有
5×4×3×2×2=240 (种).
所以不同的染色方法共有180+240=420 (种).
变式 将一个四棱锥的每个顶点染上一种颜色,使同一条棱的两端点异色,如果只有五种颜色可供使用,那么不同的染色方法总数是多少?
S
A
B
C
D
解2:
从颜色的种数进行分类:
若染5种颜色,则不同的染色方法有
5×4×3×2×1=120 (种).
(2) 若染4种颜色,则不同的染色方法有
5×4×3×2×2=240 (种).
(3) 若染3种颜色,则不同的染色方法有
5×4×3=60 (种).
所以不同的染色方法共有120+240+60=420 (种).
解:(1) 由分步计数原理得,所求三位数共有5×5×4=100个.
练习5 用0,1,2,3,4,5这6个数字:
(1)可以组成______个数字不重复的三位数;
(2)可以组成______个数字允许重复的三位数;
(3)可以组成______个大于3000,小于5421的数字不重复的四位数.
(2) 由分步计数原理得,所求三位数共有5×6×6=180个.
(3) 分四类:
①千位数字为3, 4之一时,有2×5×4×3=120个;
②千位数字为5,百位数字为0,1,2,3之一时,有4×4×3=48个;
③千位数字是5百位数字是4,十位数字是0,1之一时,有2×3=6个;
④千位数字是5百位数字是4,十位数字是2时,有1个;
所以所求四位数共有120+48+6+1=175个.
小结:
1. 分类加法计数原理:一般地,如果完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有m+n种不同的方法.
2. 分步乘法计数原理:一般地,完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有m×n种不同的方法.
特别地,如果完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法, 在第n类方案中有mn种不同的方法,那么完成这件事共有m1+m2+ +mn种不同的方法.
特别地,如果完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法, ,做第n步有mn种不同的方法,那么完成这件事共有m1×m2× ×mn种不同的方法.
6.1 分类加法计数原理与分步乘法计数原理
第六章 计数原理
汽车号牌的序号一般是从26个英文字母、10 个阿拉伯数字中选出若干个,并按适当顺序排列而成. 随着人们生活水平的提高,家庭汽车拥有量迅速增长,汽车号牌序号需要扩容. 那么,交通管理部门应如何确定序号的组成方法,才能满足民众的需求呢 这就需要“数(shu)出”某种汽车号牌序号的组成方案下所有可能的序号数,这就是计数.
日常生活、生产中类似的问题大量存在. 例如,幼儿会通过一个一个地数的方法,统计自己拥有玩具的数量;学校要举行班际篮球比赛,在确定赛制后,体育组的老师需要知道共需要举行多少场比赛;用红、黄、绿三面旗帜组成航海信号,颜色的不同排列表示不同的信号,需要知道共可以组成多少种不同的信号 如果问题中数量很少,一个一个地数也不失为一种计数的好方法. 但如果问题中数量很多,我们还一个一个地去数吗
在小学我们学了加法和乘法,这是将若干个“小”的数结合成“较大”的数最基本的方法. 这两种方法经过推广就成了本章将要学习的分类加法计数原理和分步乘法计数原理. 这两个原理是解决计数问题的最基本、最重要的方法,利用两个计数原理还可以得到两类特殊计数问题的计数公式—排列数公式和组合数公式,应用公式就可以方便地解决一些计数问题. 作为计数原理与计数公式的一个应用,本章我们还将学习在数学上有广泛应用的二项式定理.
计数问题是我们从小就经常遇到的,通过列举一个一个地数是计数的基本方法. 但当问题中的数量很大时,列举的方法效率不高. 能否设计巧妙的“数法”,以提高效率呢 下面先分析一个简单的问题,并尝试从中得出巧妙的计数方法.
思考 用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码
因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+ 10=36种不同的号码.
探究 你能说一说这个问题的特征吗
首先,这里要完成的事情是“给一个座位编号”;其次是“或”字的出现: 一个座位编号用一个英文字母或一个阿拉伯数字表示. 因为英文字母与阿拉伯数字互不相同,所以用英文字母编出的号码与用阿拉伯数字编出的号码也互不相同.这两类号码数相加就得到号码的总数.
这里的“或”代表分类.
上述计数过程的基本环节是:
(1) 确定分类标准,根据问题条件分为字母号码和数字号码两类;
(2) 分别计算各类号码的个数;
(3) 各类号码的个数相加,得出所有号码的个数.
我们把这种计数方法称为分类加法计数原理.
一般地,如果完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有
N=m+n
种不同的方法.
分类加法计数原理:
两类不同方案中的方法互不相同
例1 在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,如下表.
如果这名同学只能只能选一专业,那么他共有多少种选择?
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
解:这名同学可以选择A,B两所大学中的一所. 在A大学中有5种专业选择方法,在B大学中有4种专业选择方法. 因为没有一个强项专业是两所大学共有的,所以根据分类加法计数原理,这名同学可能的专业选择种数为
2. 在例1中,如果数学也是A大学的强项专业,那么A大学共有6个专业可以选择,B大学共有4个专业可以选择,应用分类加法计数原理,得到这名同学可能的专业选择种数为6+4=10. 这种算法有什么问题?
A大学 B大学
生物学 数学
化学 会计学
医学 信息技术学
物理学 法学
工程学
数学
解:这种算法有问题,因为问题强调的是这名同学的专业选择,故并不需要考虑学校的差异,所以这名同学可能的专业选择种数应当为
课本P5
特别地,如果完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法, 在第n类方案中有mn种不同的方法,那么完成这件事共有m1+m2+ +mn种不同的方法.
探究 如果完成一件事有三类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,在第3类方案中有m3种不同的方法,那么完成这件事共有多少种不同的方法
如果完成一件事有n类不同方案,在每一类方案中都有若干种不同的方法,那么应当如何计数呢
根据分类加法计数原理,可知完成这件事共有m1+m2+m3种不同的方法.
各类不同方案中的方法互不相同
正确理解分类(加法)计数原理:
① 分类加法计数原理针对的是“分类”问题,
② 完成一件事要分为若干类,
③ 各类的方法相互独立,
④ 各类中的各种方法也相对独立,
⑤ 用任何一类中的任何一种方法都可以单独完成这件事.
思考 用前6个大写英文字母和1~9这9个阿拉伯数字,以A1, A2, , A9, B1, B2, 的方式给教室里的一个座位编号,总共能编出多少种不同的号码
这里要完成的事情仍然是“给一个座位编号”,但与前一问题的要求不同.在前一问题中,用26个英文字母中的任意一个或10个阿拉伯数字中的任意一个,都可以给出一个座位号码. 但在这个问题中,号码必须由一个英文字母和一个作为下标的阿拉伯数字组成,即得到一个号码要经过先确定一个英文字母,后确定一个阿拉伯数字这样两个步骤. 用右图所示的方法可以列出所有可能的号码.
A
1
9
4
2
3
数字
5
7
6
8
字母
得到的号码
A1
A2
A3
A4
A5
A6
A7
A8
A9
树状图
能用树状图列出所有可能的号码吗?
由此可得,能编出的不同号码共有
上述问题要完成的一件事情仍然是“给 一个座位编号”,其中最重要的特征是“和”字的出现:一个座位编号由一个英文字母和一个阿拉伯数字构成. 因此得到一个座位号要经过先确定一个英文字母, 后确定一个阿拉伯数字这两个步骤,每一个英文字母与不同的数字组成的号码是互不相同的.
我们把上述这种计数方法称为分步乘法计数原理.
分步乘法计数原理:
一般地,完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有
N=m×n
种不同的方法.
注意:无论第1步采用哪种方法,与之对应的第2步都有相同的方法数.
特别地,如果完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法, ,做第n步有mn种不同的方法,那么完成这件事共有 种不同的方法.
正确理解分步乘法计数原理:
① 分步计数原理针对的是“分步”问题,
② 完成一件事要分为若干步,
③ 各个步骤相互依存,
④ 完成任何其中的一步都不能完成该件事,
⑤ 只有当各个步骤都完成后,才算完成这件事.
例2 某班有男生30名、女生24名,从中任选男生和女生各1名代表班级参加比赛,共有多少种不同的选法
解:第1步,从30名男生中选出1人,有30种不同选法;
第2步,从24名女生中选出1人,有24种不同选法.
根据分步乘法计数原理,共有不同选法的种数为
N=30×24= 720.
例3 书架的第 1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1) 从书架上任取1本书,有多少种不同取法
(2) 从书架的第1层、第2层、第3层各取1本书,有多少种不同取法
解:(1) 根据分类加法计数原理,不同的取法种数为
N=4+3+2=9.
(2) 根据分步乘法计数原理,不同的取法种数为
N=4×3×2= 24.
1. 填空题
(1) 一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这项工作,不同选法的种数是________;
(2) 从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同路线的条数是_________.
9
6
课本P5
3. 书架上层放有6本不同的数学书,下层放有5本不同的语文书.
(1) 从书架上任取1本书,有多少种不同的取法
(2) 从书架上任取数学书和语文书各1本,有多少种不同的取法
4. 现有高一年级的学生3名,高二年级的学生5名,高三年级的学生4名.
(1) 从三个年级的学生中任选1人参加接待外宾的活动,有多少种不同的选法
(2) 从三个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法
解:(1) 11种;(2) 30种.
解:(1) 12种;(2) 60种.
课本P6
解:从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第1步,从3幅画中选1幅挂在左边墙上,有3种选法;
第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法.
根据分步乘法计数原理,不同挂法的种数为
N=3×2=6.
这6种挂法如右图所示.
例4 要从甲、 乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法 .
乙
乙
丙
甲
右边
丙
乙
甲
左边
得到的挂法
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
甲
丙
分类加法计数原理和分步乘法计数原理,回答的都是有关做一件事的不同方法种数的问题. 区别在于:
分类加法计数原理针对的是“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事,关键词是“分类”;
分步乘法计数原理针对的是“分步”问题,各个步骤中的方法互相依存,只有每一个步骤都完成才算做完这件事,关键词是“分步”.
例5 给程序模块命名,需要用3个字符,其中首字符要求用字母A~G或U~Z,后两个要求用数字1 ~9,最多可以给多少个程序命名?
解2: 首字符用A~G给程序命名的个数为 7×9×9=567.
首字符用U~Z给程序命名的个数为 6×9×9=486.
∴总的不同名称的个数是 567+486=1053.
思考 你还能给出不同的解法吗
解: 由分类加法计数原理,首字符不同选法的种数为
7+6=13.
后两个字符从1~9中选,因为数字可以重复,所以不同选法的种数都为9.
由分步乘法计数原理,不同名称的个数是
13×9×9=1053,
即最多可以给1053个程序模块命名.
例6 电子元件很容易实现电路的通与断、电位的高与低等两种状态,而这也是最容易控制的两种状态. 因此计算机内部就采用了每一位只有0或1两种数字的记数法,即二进制. 为了使计算机能够识别字符,需要对字符进行编码,每个字符可以用1个或多个字节来表示,其中字节是计算机中数据存储的最小计量单位,每个字节由8个二进制位构成.
(1) 1个字节(8位)最多可以表示多少个不同的字符
(2) 计算机汉字国标码包含了6763个汉字,一个汉字为一个字符,要对这些汉字进行编码,每个汉字至少要用多少个字节表示
解: (1) 由分步乘法计数原理,1个字节最多可以表示不同的字符个数是
2×2×2×2×2×2×2×2=28=256.
(2) 由(1)知,1个字节最多可以表示256个不同的字符,则2个字节最多就可以表示256 ×256=65536>6763,所以每个汉字至少要用2个字节表示.
1. 某电话局管辖范围内的电话号码由8位数字组成,其中前4位的数字是不变的,后4位数字都是0~9中的一个数字,这个电话局不同的电话号码最多有多少个
解:104=10000 (个).
2. 从5名同学中选出正、副组长各1名,有多少种不同的选法
解:5×4=20 (种).
3. 从1, 2, , 19, 20中任选一个数作被减数,再从1, 2, , 10中任选一个数作减数,然后写成一个减法算式,共可得到多少个不同的算式
解:20×10=200 (个).
课本P7
解1:被5除余2的正整数的个位是2或7.
当满足条件的数是一位数时,满足条件的个数有2个 ;
当满足条件的数是两位数时,满足条件的个数有9×2=18个 ;
当满足条件的数是三位数时,满足条件的个数有4×10×2= 80个 .
所以满足条件的数共有100个.
4. 在1, 2, , 500中,被5除余2的数共有多少个
解2:被5除余2的数可以表示为5k+2 (k为整数).
由1≤5k+2≤500,解得0≤k≤99,
满足条件的k值有100个, 所以满足条件的数共有100个.
解:满足条件的三位数有5×5×5= 125 个 .
5. 由数字1, 2, 3, 4, 5可以组成多少个三位数(各位上的数字可以重复)
课本P7
例7 计算机编程人员在编写好程序以后需要对程序进行测试. 程序员需要知道到底有多少条执行路径(程序从开始到结束的路线),以便知道需要提供多少个测试数据. 一般地,一个程序模块由许多子模块组成. 下图是一个具有许多执行路径的程序模块,它有多少条执行路径
另外,为了减少测试时间,程序员需要设法减少测试次数. 你能帮助程序员设计一个测试方法,以减少测试次数吗
解:由程序模块可得,执行路径条数有
(18+45+28)×(38+43)=7371.
为了减少测试次数,可单独测试5个模块和模块1,2,3与模块4,5之间的信息交流是否正常即可,这样测试的次数只有
(18+45+28 +38 +43)×(3×2)=178 (次).
例8 通常, 我国民用汽车号牌的编号由两部分组成: 第一部分为用汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.
其中,序号的编码规则为:
(1) 由10个阿拉伯数字和除O,I之外的24个英文字母组成;
(2) 最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,那
么这个发牌机关最多能发放多少张汽车号牌
解:当序号中没有字母时,号牌张数为 105=100000.
当序号中有1位字母时,号牌张数为5×24×104=1200000.
当序号中有2位字母时,号牌张数为10×242×103=5760000.
所以这个发牌机关最多能发的汽车号牌张数为7060000.
归纳:
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析两点:
(1) 要完成的“一件事”是什么;
(2) 需要分类还是需要分步.
分类要做到“不重不漏”. 分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”,即完成了所有步骤,恰好完成任务. 分步后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
解:展开后共有3×3×5=45项.
1. 乘积(a1+a2+a3)(b1+b2+b3)(c1+c2+c3+c4+c5) 展开后共有多少项
解:9+8+7+6+5+4+3+2+1=45 (个).
2. 在所有的两位数中,个位数字小于十位数字的有多少个
3. 某商场有6个门,如果某人从其中的任意一个门进人商场,并且要求从其他的门出去,那么共有多少种不同的进出商场的方式
解:进出商场的不同方式有6×5=30(种).
4.任意画一条直线,在直线上任取n个分点.
(1) 从这n个分点中任取2个点形成一条线段,可得到多少条线段
(2) 从这n个分点中任取2个点形成一个向量,可得到多少个向量
解:
课本P11
练习2 运动会有跳高、跑步、游泳三个比赛项目,某班有四名同学报名参赛,要求每名同学只能参加一个项目,不同的报名方式共有( )
A. 4种 B. 24种 C. 43种 D. 34种
练习1 四名同学,争夺三项冠军(每项没有并列冠军),则冠军获得者可能有的种类是( )
A. 4 B. 24 C. 43 D. 34
C
D
练习3 现有高一学生9人,高二学生12人,高三学生7人,自发组织数学课外活动小组,从中推选两名来自不同年级的学生做一次活动的主持人,有_____种不同选法.
解:
推选两名来自不同年级的学生做一次活动主持人,有不同选法:
9×12 +12×7 +9×7
= 255(种).
练习4 长方形的两条对角线把长方形分成四部分,如图用五种不同的颜色给这四部分涂色,每一部分涂一种颜色,任何相邻(具有公共边)的两部分涂不同颜色,问有多少种不同的涂色方法?
A
B
C
D
解1:
若A, C同色,则不同的涂色方法有
5×4×4=80 (种).
(2) 若A, C不同色,则不同的涂色方法有
5×4×3×3=180 (种).
综上所述,由分类计数原理得:
共有80+180=260 (种).
练习4 长方形的两条对角线把长方形分成四部分,如图用五种不同的颜色给这四部分涂色,每一部分涂一种颜色,任何相邻(具有公共边)的两部分涂不同颜色,问有多少种不同的涂色方法?
A
B
C
D
解2:
由题意四部分最多涂4种颜色,最少涂2种颜色,
若涂4种颜色,则不同的涂色方法有
5×4×3×2=120 (种).
(2) 若涂3种颜色,则不同的涂色方法有
5×4×3×2=120 (种).
(3) 若涂2种颜色,则不同的涂色方法有
5×4=20 (种).
综上所述,由分类计数原理得:
共有120+120+20=260 (种).
解1:
变式 将一个四棱锥的每个顶点染上一种颜色,使同一条棱的两端点异色,如果只有五种颜色可供使用,那么不同的染色方法总数是多少?
S
A
B
C
D
若A, C同色,则不同的染色方法有
5×4×3×3=180 (种).
(2) 若A, C不同色,则不同的染色方法有
5×4×3×2×2=240 (种).
所以不同的染色方法共有180+240=420 (种).
变式 将一个四棱锥的每个顶点染上一种颜色,使同一条棱的两端点异色,如果只有五种颜色可供使用,那么不同的染色方法总数是多少?
S
A
B
C
D
解2:
从颜色的种数进行分类:
若染5种颜色,则不同的染色方法有
5×4×3×2×1=120 (种).
(2) 若染4种颜色,则不同的染色方法有
5×4×3×2×2=240 (种).
(3) 若染3种颜色,则不同的染色方法有
5×4×3=60 (种).
所以不同的染色方法共有120+240+60=420 (种).
解:(1) 由分步计数原理得,所求三位数共有5×5×4=100个.
练习5 用0,1,2,3,4,5这6个数字:
(1)可以组成______个数字不重复的三位数;
(2)可以组成______个数字允许重复的三位数;
(3)可以组成______个大于3000,小于5421的数字不重复的四位数.
(2) 由分步计数原理得,所求三位数共有5×6×6=180个.
(3) 分四类:
①千位数字为3, 4之一时,有2×5×4×3=120个;
②千位数字为5,百位数字为0,1,2,3之一时,有4×4×3=48个;
③千位数字是5百位数字是4,十位数字是0,1之一时,有2×3=6个;
④千位数字是5百位数字是4,十位数字是2时,有1个;
所以所求四位数共有120+48+6+1=175个.
小结:
1. 分类加法计数原理:一般地,如果完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有m+n种不同的方法.
2. 分步乘法计数原理:一般地,完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有m×n种不同的方法.
特别地,如果完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法, 在第n类方案中有mn种不同的方法,那么完成这件事共有m1+m2+ +mn种不同的方法.
特别地,如果完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法, ,做第n步有mn种不同的方法,那么完成这件事共有m1×m2× ×mn种不同的方法.
