2021-2022学年高二下学期数学人教A版(2019)必修第三册6.2.4组合数课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)必修第三册6.2.4组合数课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
6.2.4 组合数
类比排列数,我们引进组合数概念:
组合数:
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
组合的第一个字母
元素总数
取出元素数
m,n所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
例如,从3个不同元素中任取2个元素的组合数为
从4个不同元素中任取3个元素的组合数为
符号 中的C是英文combination
(组合)的第一个字母. 组合数还可以用符号 表示.
思考:
探究 前面已经提到,组合和排列有关系,我们能否利用这种关系,由排列数 来求组合数 呢
3个不同元素a, b, c中取出2个共有ab, ac, bc 3个不同的组合,
4个不同元素a, b, c, d中取出3个共有abc, abd, acd, bcd 4个不同的组合,
4个不同元素a, b, c, d中取出3个元素的排列数为
3个不同元素a, b, c中取出2个元素的排列数为
下面我们就来探究
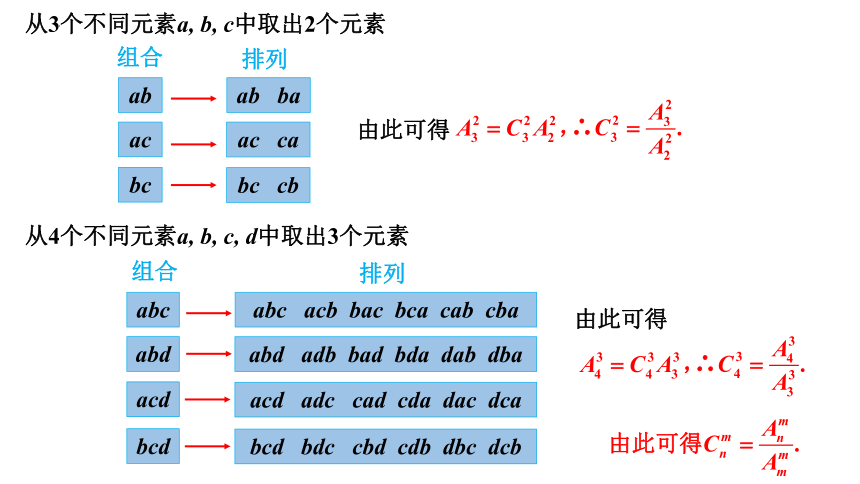
从3个不同元素a, b, c中取出2个元素
从4个不同元素a, b, c, d中取出3个元素
组合
ab
排列
ac
bc
ab ba
ac ca
bc cb
由此可得
组合
abc
排列
abd
acd
abc acb bac bca cab cba
abd adb bad bda dab dba
acd adc cad cda dac dca
bcd
bcd bdc cbd cdb dbc dcb
由此可得
这里的n, m∈N*,并且m≤n,这个公式叫做组合数公式.
组合数公式:
另外,我们规定
所以上面的公式还可以写成
解:
例6 计算:
思考 此关系是否具有一般性?
性质1
性质2
性质1
性质2
组合数的性质:
解:
1. 计算:
课本P25
证明:
2. 求证:
课本P25
巩固训练:
1. 计算:
解:
解:
解:
证明:
解:
例7 在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1) 有多少种不同的抽法
(2) 抽出的3件中恰好有1件是次品的抽法有多少种
(3) 抽出的3件中至少有1件是次品的抽法有多少种
解:
(1) 所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2) 从2件次品中抽出1件的抽法有 种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
例7 在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1) 有多少种不同的抽法
(2) 抽出的3件中恰好有1件是次品的抽法有多少种
(3) 抽出的3件中至少有1件是次品的抽法有多少种
解1(直接法):
解2(间接法):
抽出的3 件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
3. 有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩,现要从中选3门考试成绩.
(1) 共有多少种不同的选法
(2) 如果物理和化学恰有1门被选,那么共有多少种不同的选法
(3) 如果物理和化学至少有1门被选,那么共有多少种不同的选法
解:
课本P25
巩固训练 从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(1) A、B必须当选;
(2) A、B都不当选;
(3) A、B不全当选;
(4) 至少有2名女生当选;
(5) 选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
解:(1) 除A、B当选外,再从其它10个人中选3人,不同的选法种数有
(2) A、B 都不当选的选法种数有
解:
(3) A、B不全当选的选法种数有
巩固训练 从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(3) A、B不全当选;
(4) 至少有2名女生当选;
(4) 至少有2名女生当选的选法种数有
(5) 选出一个男生担任体育班委,再选出1名女生担任文娱班委,剩下的10人中任取3人担任其它3个班委.
由分步计数原理可得到所有方法总数为
解:
巩固训练 从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(5) 选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
平均分成的每一组,不管它们的顺序如何,都是一种情况,所以分组后要除以组数的全排列,即
例1 把abcd分成平均两组,共有_____种分法.
ab
cd
ac
bd
ad
bc
cd
bd
bc
ad
ac
ab
这两个在分组时只能算一个,故分组方法有
排列组合中的分堆问题—平均分组问题
3
变式 把6人分成平均三组,共有_____种分法.
15
总结:
1. 均分不安排任务的问题
例2 现有12本不同的书.
(1)按4∶4∶4平均分成三堆有多少种不同的分法?
(2)按2∶2∶2∶6分成四堆有多少种不同的分法?
解:
2. 分堆安排工作的问题
例3(1)6本不同的书按2∶2∶2平均分给甲、乙、丙三个人,有 多少种不同的分法?
(2)12支笔按3:3:2:2:2分给A、B、C、D、E五个人有多少种不同的分法?
解:
例4 现有6本不同的书.
(1) 按1:2:3分成三堆有多少种不同的分法?
(2) 按1:2:3分给甲、乙、丙三个人有多少种不同的分法?
4. 非均分组问题
解:
变式 有六本不同的书分给甲、乙、丙三名同学,按下条件,各有多少种不同的分法?
(1)每人各得两本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人一本,一人两本,一人三本;
(4)甲得四本,乙得一本,丙得一本;
(5)一人四本,另两人各一本·
4. 非均分组问题
解:
小结:
1. 组合数公式:
规定
性质1
性质2
2. 组合数的性质:
6.2.4 组合数
类比排列数,我们引进组合数概念:
组合数:
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用符号 表示.
组合的第一个字母
元素总数
取出元素数
m,n所满足的条件是:
(1) m∈N*,n∈N* ;
(2) m≤n .
例如,从3个不同元素中任取2个元素的组合数为
从4个不同元素中任取3个元素的组合数为
符号 中的C是英文combination
(组合)的第一个字母. 组合数还可以用符号 表示.
思考:
探究 前面已经提到,组合和排列有关系,我们能否利用这种关系,由排列数 来求组合数 呢
3个不同元素a, b, c中取出2个共有ab, ac, bc 3个不同的组合,
4个不同元素a, b, c, d中取出3个共有abc, abd, acd, bcd 4个不同的组合,
4个不同元素a, b, c, d中取出3个元素的排列数为
3个不同元素a, b, c中取出2个元素的排列数为
下面我们就来探究
从3个不同元素a, b, c中取出2个元素
从4个不同元素a, b, c, d中取出3个元素
组合
ab
排列
ac
bc
ab ba
ac ca
bc cb
由此可得
组合
abc
排列
abd
acd
abc acb bac bca cab cba
abd adb bad bda dab dba
acd adc cad cda dac dca
bcd
bcd bdc cbd cdb dbc dcb
由此可得
这里的n, m∈N*,并且m≤n,这个公式叫做组合数公式.
组合数公式:
另外,我们规定
所以上面的公式还可以写成
解:
例6 计算:
思考 此关系是否具有一般性?
性质1
性质2
性质1
性质2
组合数的性质:
解:
1. 计算:
课本P25
证明:
2. 求证:
课本P25
巩固训练:
1. 计算:
解:
解:
解:
证明:
解:
例7 在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1) 有多少种不同的抽法
(2) 抽出的3件中恰好有1件是次品的抽法有多少种
(3) 抽出的3件中至少有1件是次品的抽法有多少种
解:
(1) 所有的不同抽法种数,就是从100件产品中抽出3件的组合数,所以抽法种数为
(2) 从2件次品中抽出1件的抽法有 种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
例7 在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件.
(1) 有多少种不同的抽法
(2) 抽出的3件中恰好有1件是次品的抽法有多少种
(3) 抽出的3件中至少有1件是次品的抽法有多少种
解1(直接法):
解2(间接法):
抽出的3 件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
3. 有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩,现要从中选3门考试成绩.
(1) 共有多少种不同的选法
(2) 如果物理和化学恰有1门被选,那么共有多少种不同的选法
(3) 如果物理和化学至少有1门被选,那么共有多少种不同的选法
解:
课本P25
巩固训练 从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(1) A、B必须当选;
(2) A、B都不当选;
(3) A、B不全当选;
(4) 至少有2名女生当选;
(5) 选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
解:(1) 除A、B当选外,再从其它10个人中选3人,不同的选法种数有
(2) A、B 都不当选的选法种数有
解:
(3) A、B不全当选的选法种数有
巩固训练 从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(3) A、B不全当选;
(4) 至少有2名女生当选;
(4) 至少有2名女生当选的选法种数有
(5) 选出一个男生担任体育班委,再选出1名女生担任文娱班委,剩下的10人中任取3人担任其它3个班委.
由分步计数原理可得到所有方法总数为
解:
巩固训练 从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(5) 选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
平均分成的每一组,不管它们的顺序如何,都是一种情况,所以分组后要除以组数的全排列,即
例1 把abcd分成平均两组,共有_____种分法.
ab
cd
ac
bd
ad
bc
cd
bd
bc
ad
ac
ab
这两个在分组时只能算一个,故分组方法有
排列组合中的分堆问题—平均分组问题
3
变式 把6人分成平均三组,共有_____种分法.
15
总结:
1. 均分不安排任务的问题
例2 现有12本不同的书.
(1)按4∶4∶4平均分成三堆有多少种不同的分法?
(2)按2∶2∶2∶6分成四堆有多少种不同的分法?
解:
2. 分堆安排工作的问题
例3(1)6本不同的书按2∶2∶2平均分给甲、乙、丙三个人,有 多少种不同的分法?
(2)12支笔按3:3:2:2:2分给A、B、C、D、E五个人有多少种不同的分法?
解:
例4 现有6本不同的书.
(1) 按1:2:3分成三堆有多少种不同的分法?
(2) 按1:2:3分给甲、乙、丙三个人有多少种不同的分法?
4. 非均分组问题
解:
变式 有六本不同的书分给甲、乙、丙三名同学,按下条件,各有多少种不同的分法?
(1)每人各得两本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人一本,一人两本,一人三本;
(4)甲得四本,乙得一本,丙得一本;
(5)一人四本,另两人各一本·
4. 非均分组问题
解:
小结:
1. 组合数公式:
规定
性质1
性质2
2. 组合数的性质:
