2021-2022学年高二下学期数学人教A版(2019)必修第三册6.3.2二项式系数的性质课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)必修第三册6.3.2二项式系数的性质课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 421.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 10:24:47 | ||
图片预览

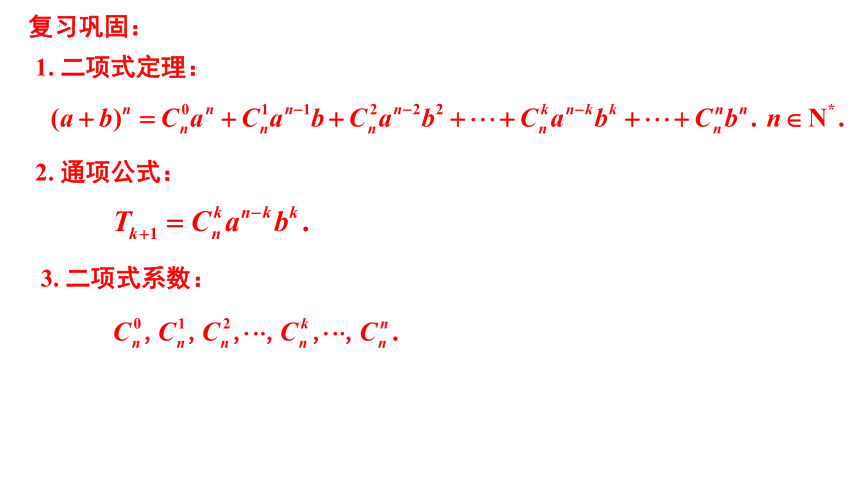




文档简介
(共19张PPT)
6.3.2 二项式系数的性质
1. 二项式定理:
复习巩固:
2. 通项公式:
3. 二项式系数:
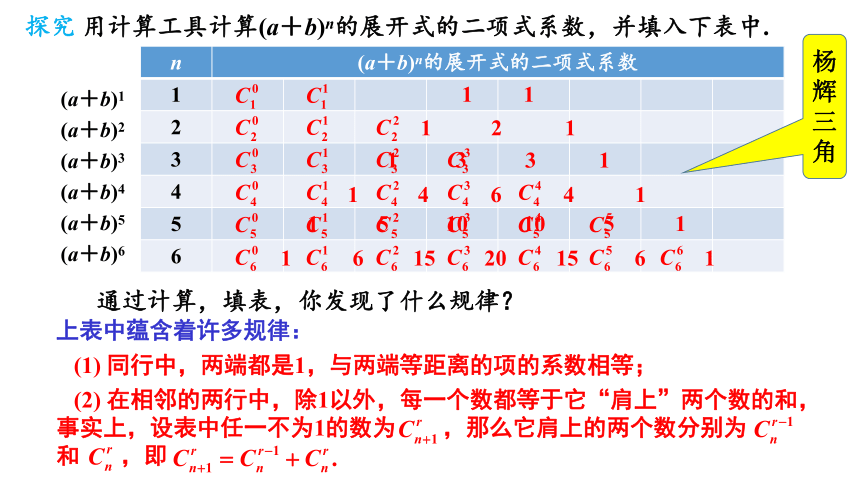
探究 用计算工具计算(a+b)n的展开式的二项式系数,并填入下表中.
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
通过计算,填表,你发现了什么规律?
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
杨辉三角
上表中蕴含着许多规律:
(1) 同行中,两端都是1,与两端等距离的项的系数相等;
(2) 在相邻的两行中,除1以外,每一个数都等于它“肩上”两个数的和,事实上,设表中任一不为1的数为 ,那么它肩上的两个数分别为 和 ,即
对于 展开式的二项式系数
从函数角度看, 可看成是以r为自变量的函数 ,其定义域是
下面从函数角度分析二项式系数:
对于确定的n,我们还可以画出它的图象. 例如,当n=6时,函数 的图象是右图中的7个孤立点.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
1. 对称性
由此我们可得二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
事实上,这一性质可直接由公式 得到.
图象的对称轴为
2. 增减性与最大值
由此我们可得二项式系数有以下性质:
3. 各二项式系数的和
由此我们可得二项式系数有以下性质:
思考
即
这就是说,(a+b)n的展开式的各二项式系数的和等于
例3 求证:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
证明:
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
思考
解:
课本34页
证明:
课本34页
课本34页
n
1
2
3
4
5
6
7
8
9
10
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
解:
课本34页
巩固训练1 在 的展开式中,第5、6、7三项系数成等差数列,求展开式中系数最大的项.
解:
由题意得
解得 n=7或14 .
①当 n=7 时,
展开式中系数最大的项是第4项与第5项,
即为
②当 n=14 时,
展开式中系数最大的项是第8项,
即为
巩固训练2 已知 的展开式中,第4项的二项式系数是倒数第2项的二项式系数的7倍,求展开式中二项式系数最大的项和系数最大的项.
解:依题意
整理得
∴ 展开式中二项式系数最大的项为
设展开式中第r+1项的系数最大,则
得
∴展开式中系数最大的项为
(1)证明:
∴ 1110 -1 能被100整除.
巩固训练3
(1) 求证:1110 -1 能被100整除.
(2) 求7777-7 被19除所得的余数.
(2) 解:
∴ 7777-7被19除所得的余数是 19-6=13.
巩固训练3
(1) 求证:1110 -1 能被100整除.
(2) 求7777-7 被19除所得的余数.
变式 求 1090 除以 7 的余数 .
解:
展开式中除末项外,均能被 7 整除 ,
其末项为 :
展开式中除末项外,均能被 7 整除 ,
故 1090 除以 7 的余数为 1 .
且末项为1,
解2:
∴展开式中除末项外,均能被 7 整除 ,
故 1090 除以 7 的余数为 1 .
而末项为1,
1. 对称性:
二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式 得到.
小结:
2. 增减性与最大值
3. 各二项式系数的和
6.3.2 二项式系数的性质
1. 二项式定理:
复习巩固:
2. 通项公式:
3. 二项式系数:
探究 用计算工具计算(a+b)n的展开式的二项式系数,并填入下表中.
n (a+b)n的展开式的二项式系数 1
2
3
4
5
6
通过计算,填表,你发现了什么规律?
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
杨辉三角
上表中蕴含着许多规律:
(1) 同行中,两端都是1,与两端等距离的项的系数相等;
(2) 在相邻的两行中,除1以外,每一个数都等于它“肩上”两个数的和,事实上,设表中任一不为1的数为 ,那么它肩上的两个数分别为 和 ,即
对于 展开式的二项式系数
从函数角度看, 可看成是以r为自变量的函数 ,其定义域是
下面从函数角度分析二项式系数:
对于确定的n,我们还可以画出它的图象. 例如,当n=6时,函数 的图象是右图中的7个孤立点.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
1. 对称性
由此我们可得二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
r
f(r)
O
1
2
3
5
10
15
20
4
5
6
事实上,这一性质可直接由公式 得到.
图象的对称轴为
2. 增减性与最大值
由此我们可得二项式系数有以下性质:
3. 各二项式系数的和
由此我们可得二项式系数有以下性质:
思考
即
这就是说,(a+b)n的展开式的各二项式系数的和等于
例3 求证:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
证明:
即在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
思考
解:
课本34页
证明:
课本34页
课本34页
n
1
2
3
4
5
6
7
8
9
10
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
解:
课本34页
巩固训练1 在 的展开式中,第5、6、7三项系数成等差数列,求展开式中系数最大的项.
解:
由题意得
解得 n=7或14 .
①当 n=7 时,
展开式中系数最大的项是第4项与第5项,
即为
②当 n=14 时,
展开式中系数最大的项是第8项,
即为
巩固训练2 已知 的展开式中,第4项的二项式系数是倒数第2项的二项式系数的7倍,求展开式中二项式系数最大的项和系数最大的项.
解:依题意
整理得
∴ 展开式中二项式系数最大的项为
设展开式中第r+1项的系数最大,则
得
∴展开式中系数最大的项为
(1)证明:
∴ 1110 -1 能被100整除.
巩固训练3
(1) 求证:1110 -1 能被100整除.
(2) 求7777-7 被19除所得的余数.
(2) 解:
∴ 7777-7被19除所得的余数是 19-6=13.
巩固训练3
(1) 求证:1110 -1 能被100整除.
(2) 求7777-7 被19除所得的余数.
变式 求 1090 除以 7 的余数 .
解:
展开式中除末项外,均能被 7 整除 ,
其末项为 :
展开式中除末项外,均能被 7 整除 ,
故 1090 除以 7 的余数为 1 .
且末项为1,
解2:
∴展开式中除末项外,均能被 7 整除 ,
故 1090 除以 7 的余数为 1 .
而末项为1,
1. 对称性:
二项式系数有以下性质:
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式 得到.
小结:
2. 增减性与最大值
3. 各二项式系数的和
