2021-2022学年高二下学期数学人教A版(2019)必修第三册7.1.1条件概率课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)必修第三册7.1.1条件概率课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 466.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 10:25:24 | ||
图片预览







文档简介
(共24张PPT)
第七章 随机变量及其分布
概率是随机事件发生可能性大小的度量. 在必修课程的概率学习中,我们结合古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质. 本章将在此基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式和全概率公式,并用它们计算较复杂事件的概率.
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章我们还将把随机试验的结果数量化,引入随机变量的概念. 对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究. 对于连续型随机变量,我们只研究服从正态分布的情况. 通过用随机变量描述和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点.
7.1 条件概率与全概率公式
7.1.1 条件概率
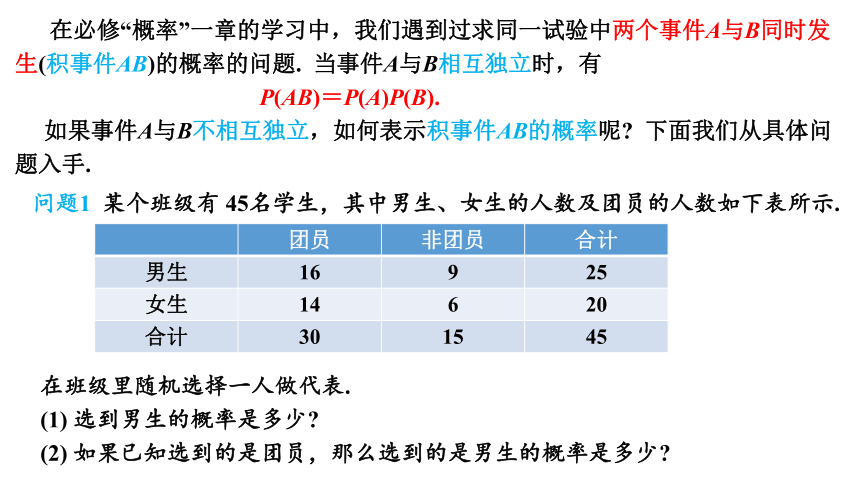
在必修“概率”一章的学习中,我们遇到过求同一试验中两个事件A与B同时发生(积事件AB)的概率的问题. 当事件A与B相互独立时,有
P(AB)=P(A)P(B).
如果事件A与B不相互独立,如何表示积事件AB的概率呢 下面我们从具体问题入手.
问题1 某个班级有 45名学生,其中男生、女生的人数及团员的人数如下表所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1) 选到男生的概率是多少
(2) 如果已知选到的是团员,那么选到的是男生的概率是多少
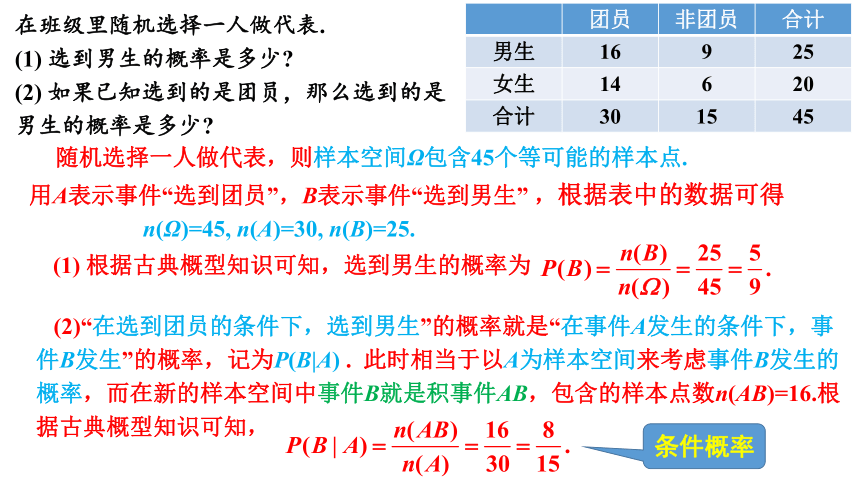
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1) 选到男生的概率是多少
(2) 如果已知选到的是团员,那么选到的是男生的概率是多少
随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.
(2)“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A) . 此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
条件概率
用A表示事件“选到团员”,B表示事件“选到男生” ,根据表中的数据可得
n(Ω)=45, n(A)=30, n(B)=25.
(1) 根据古典概型知识可知,选到男生的概率为
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭、随机选择一个家庭,那么
(1) 该家庭中两个小孩都是女孩的概率是多大
(2) 如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大
用a表示男孩,b表示女孩,则样本空间Ω={aa, ab, ba, bb},且所有样本点是等可能的.
(2)“在选择的家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A) . 此时A成为样本空间,事件B就是积事件AB,根据古典概型知识可知,
条件概率
用A表示事件“选择的家庭中有女孩”,B表示事件“选择的家庭中两个小孩都是女孩”,则
A={ab, ba, bb},B={bb}.
(1) 根据古典概型知识可得,两个小孩都是女孩的概率为
在上面两个问题中,在事件A发生的条件下,事件B发生的概率都是
这个结论对于一般的古典概型仍然成立. 事实上,如图所示,若已知事件A发生,则A成为样本空间. 此时,事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值,即
∴在事件A发生的条件下,事件B发生的概率还可以通过 来计算.
条件概率:
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
由这个定义可知,对任意两个事件A,B,若P(A)>0,则有
我们称上式为为概率的乘法公式.
探究 在问题1和问题2中,都有P(B|A) ≠ P(B). 一般地,P(B|A)与P(B)不一定相等. 如果P(B|A)与P(B)相等,那么事件A与B应满足什么条件
直观上看,当事件A与B相互独立时,事件A发生与否不影响事件B发生的概率,这等价于P(B|A)=P(B)成立.
事实上,若事件A与B相互独立,即P(AB)=P(A)P(B),且P(A)>0,则
反之,若P(B|A)=P(B),且P(A)>0,则
即事件A与B相互独立.
因此当P(A)>0 时,当且仅当事件A与B相互独立时,有P(B|A)=P(B)成立.
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB. 从5道试题中每次不放回地随机抽取2道,则
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1) 第1次抽到代数题且第2次抽到几何题的概率;
(2) 在第1次抽到代数题的条件下,第2次抽到几何题的概率.
设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
解:
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率. 由于
已知第1次抽到代数题,这时还余下4道试题,其中代数题和几何题各2道. 因此,事件A发生的条件下,事件B发生的概率为
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1) 第1次抽到代数题且第2次抽到几何题的概率;
(2) 在第1次抽到代数题的条件下,第2次抽到几何题的概率.
解法2:(在缩小的样本空间A上求P(B | A))
设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
∴第1次抽到代数题且第2次抽到几何题的概率为
从例1可知,求条件概率有两种方法:
① 是基于样本空间Ω,先计算P(A)和P(AB),再利用条件概率公式求P(B|A);
② 是根据条件概率的直观意义, 增加了“A发生”的条件后, 样本空间缩小为A, 求P(B|A)就是以A为样本空间计算AB的概率.
条件概率只是缩小了样本空间, 因此条件概率同样具有概率的性质.
设P(A)>0,则条件概率的性质为:
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张. 他们中奖的概率与抽奖的次序有关吗
解:
用A,B,C分别表示甲、乙、丙中奖的事件,则
事实上,在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例3 银行储蓄卡的密码由 6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求:
(1) 任意按最后1位数字,不超过2次就按对的概率;
(2) 如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:
(1) 设Ai=“第i次按对密码”(i=1, 2),则事件“不超过2次就按对密码”可表示为
(2) 设B=“最后1位密码为偶数”,则
解:
课本48页
由此可得,
A发生,则B一定发生
2. 从一副不含大小王的52张扑克牌中,每次从中随机抽出1张扑克牌,抽出的牌不再放回,已知第1次抽到A牌,求第2次抽到A牌的概率.
设第1次抽到A牌为事件A,第2次抽到A牌为事件B,则
解:
∴在第1次抽到A牌的条件下,第2次抽到A牌的概率为
3. 袋子中有10个大小相同的小球,其中7个白球,3个黑球. 每次从袋子中随机摸出1个球,摸出的球不再放回. 求:
(1) 在第1次摸到白球的条件下,第2次摸到白球的概率;
(2) 两次都摸到白球的概率.
设第1次摸到白球为事件A,第2次摸到白球为事件B,则
解:
∴在第1次摸到白球的条件下,第2次摸到白球的概率为
∴两次都摸到白球的概率为
说 明:
概率P(B|A)与P(AB)的区别与联系:
联系:事件A, B都发生了.
区别:
(1) 在P(B|A)中,事件A, B发生有时间上的差异,A先B后;在P(AB)中,事件A, B同时发生.
(2) 样本空间不同,在P(B|A)中,事件A成为样本空间;在P(AB)中,样本空间仍为Ω. 因此有P(B|A) ≥ P(AB).
小结:
1. 条件概率:
在事件A发生的条件下,事件B发生的条件概率,简称条件概率,记作
由条件概率公式可得
2. 乘法公式:
第七章 随机变量及其分布
概率是随机事件发生可能性大小的度量. 在必修课程的概率学习中,我们结合古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质. 本章将在此基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式和全概率公式,并用它们计算较复杂事件的概率.
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章我们还将把随机试验的结果数量化,引入随机变量的概念. 对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究. 对于连续型随机变量,我们只研究服从正态分布的情况. 通过用随机变量描述和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点.
7.1 条件概率与全概率公式
7.1.1 条件概率
在必修“概率”一章的学习中,我们遇到过求同一试验中两个事件A与B同时发生(积事件AB)的概率的问题. 当事件A与B相互独立时,有
P(AB)=P(A)P(B).
如果事件A与B不相互独立,如何表示积事件AB的概率呢 下面我们从具体问题入手.
问题1 某个班级有 45名学生,其中男生、女生的人数及团员的人数如下表所示.
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1) 选到男生的概率是多少
(2) 如果已知选到的是团员,那么选到的是男生的概率是多少
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1) 选到男生的概率是多少
(2) 如果已知选到的是团员,那么选到的是男生的概率是多少
随机选择一人做代表,则样本空间Ω包含45个等可能的样本点.
(2)“在选到团员的条件下,选到男生”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A) . 此时相当于以A为样本空间来考虑事件B发生的概率,而在新的样本空间中事件B就是积事件AB,包含的样本点数n(AB)=16.根据古典概型知识可知,
条件概率
用A表示事件“选到团员”,B表示事件“选到男生” ,根据表中的数据可得
n(Ω)=45, n(A)=30, n(B)=25.
(1) 根据古典概型知识可知,选到男生的概率为
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭、随机选择一个家庭,那么
(1) 该家庭中两个小孩都是女孩的概率是多大
(2) 如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大
用a表示男孩,b表示女孩,则样本空间Ω={aa, ab, ba, bb},且所有样本点是等可能的.
(2)“在选择的家庭有女孩的条件下,两个小孩都是女孩”的概率就是“在事件A发生的条件下,事件B发生”的概率,记为P(B|A) . 此时A成为样本空间,事件B就是积事件AB,根据古典概型知识可知,
条件概率
用A表示事件“选择的家庭中有女孩”,B表示事件“选择的家庭中两个小孩都是女孩”,则
A={ab, ba, bb},B={bb}.
(1) 根据古典概型知识可得,两个小孩都是女孩的概率为
在上面两个问题中,在事件A发生的条件下,事件B发生的概率都是
这个结论对于一般的古典概型仍然成立. 事实上,如图所示,若已知事件A发生,则A成为样本空间. 此时,事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值,即
∴在事件A发生的条件下,事件B发生的概率还可以通过 来计算.
条件概率:
一般地,设A,B为两个随机事件,且P(A)>0,我们称
为在事件A发生的条件下,事件B发生的条件概率,简称条件概率.
由这个定义可知,对任意两个事件A,B,若P(A)>0,则有
我们称上式为为概率的乘法公式.
探究 在问题1和问题2中,都有P(B|A) ≠ P(B). 一般地,P(B|A)与P(B)不一定相等. 如果P(B|A)与P(B)相等,那么事件A与B应满足什么条件
直观上看,当事件A与B相互独立时,事件A发生与否不影响事件B发生的概率,这等价于P(B|A)=P(B)成立.
事实上,若事件A与B相互独立,即P(AB)=P(A)P(B),且P(A)>0,则
反之,若P(B|A)=P(B),且P(A)>0,则
即事件A与B相互独立.
因此当P(A)>0 时,当且仅当事件A与B相互独立时,有P(B|A)=P(B)成立.
(1)“第1次抽到代数题且第2次抽到几何题”就是事件AB. 从5道试题中每次不放回地随机抽取2道,则
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1) 第1次抽到代数题且第2次抽到几何题的概率;
(2) 在第1次抽到代数题的条件下,第2次抽到几何题的概率.
设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
解:
(2)“在第1次抽到代数题的条件下,第2次抽到几何题”的概率就是事件A发生的条件下,事件B发生的概率. 由于
已知第1次抽到代数题,这时还余下4道试题,其中代数题和几何题各2道. 因此,事件A发生的条件下,事件B发生的概率为
例1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回. 求:
(1) 第1次抽到代数题且第2次抽到几何题的概率;
(2) 在第1次抽到代数题的条件下,第2次抽到几何题的概率.
解法2:(在缩小的样本空间A上求P(B | A))
设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
∴第1次抽到代数题且第2次抽到几何题的概率为
从例1可知,求条件概率有两种方法:
① 是基于样本空间Ω,先计算P(A)和P(AB),再利用条件概率公式求P(B|A);
② 是根据条件概率的直观意义, 增加了“A发生”的条件后, 样本空间缩小为A, 求P(B|A)就是以A为样本空间计算AB的概率.
条件概率只是缩小了样本空间, 因此条件概率同样具有概率的性质.
设P(A)>0,则条件概率的性质为:
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张. 他们中奖的概率与抽奖的次序有关吗
解:
用A,B,C分别表示甲、乙、丙中奖的事件,则
事实上,在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例3 银行储蓄卡的密码由 6位数字组成. 某人在银行自助取款机上取钱时,忘记了密码的最后1位数字. 求:
(1) 任意按最后1位数字,不超过2次就按对的概率;
(2) 如果记得密码的最后1位是偶数,不超过2次就按对的概率.
解:
(1) 设Ai=“第i次按对密码”(i=1, 2),则事件“不超过2次就按对密码”可表示为
(2) 设B=“最后1位密码为偶数”,则
解:
课本48页
由此可得,
A发生,则B一定发生
2. 从一副不含大小王的52张扑克牌中,每次从中随机抽出1张扑克牌,抽出的牌不再放回,已知第1次抽到A牌,求第2次抽到A牌的概率.
设第1次抽到A牌为事件A,第2次抽到A牌为事件B,则
解:
∴在第1次抽到A牌的条件下,第2次抽到A牌的概率为
3. 袋子中有10个大小相同的小球,其中7个白球,3个黑球. 每次从袋子中随机摸出1个球,摸出的球不再放回. 求:
(1) 在第1次摸到白球的条件下,第2次摸到白球的概率;
(2) 两次都摸到白球的概率.
设第1次摸到白球为事件A,第2次摸到白球为事件B,则
解:
∴在第1次摸到白球的条件下,第2次摸到白球的概率为
∴两次都摸到白球的概率为
说 明:
概率P(B|A)与P(AB)的区别与联系:
联系:事件A, B都发生了.
区别:
(1) 在P(B|A)中,事件A, B发生有时间上的差异,A先B后;在P(AB)中,事件A, B同时发生.
(2) 样本空间不同,在P(B|A)中,事件A成为样本空间;在P(AB)中,样本空间仍为Ω. 因此有P(B|A) ≥ P(AB).
小结:
1. 条件概率:
在事件A发生的条件下,事件B发生的条件概率,简称条件概率,记作
由条件概率公式可得
2. 乘法公式:
