青岛版三年级下册数学 智慧广场-植树问题 教案
文档属性
| 名称 | 青岛版三年级下册数学 智慧广场-植树问题 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 351.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 09:39:01 | ||
图片预览


文档简介
青岛版小学数学三年级下册《智慧广场-植树问题》教学设计
【教学目标】
1.结合植树问题的情境,借助生活经验和画图的策略学习并掌握植树问题的规律。
2.学生在丰富的素材中,经历观察、操作、分析等寻找规律的过程,初步培养学生从实际问题中探索规律,找出解决问题的有效方法的能力。
3.学生在充分的自主探索,合作交流中,增强探究的欲望,体验成功的喜悦,感受数学的魅力。
【教学重点】建立植树问题的模型并掌握其规律。
【教学难点】能根据不同情况选择正确方法解决植树问题。
【教学准备】学习单、板贴。
【教学过程】
一、创设情境,导入新课。
1.同学们,喜欢猜谜语吗?老师给大家带来一个谜语(课件出示):两棵小树十个杈,不长叶子不开花,能写会算还会画,天天干活不说话。
2.请同学们伸出你的左手,分开五指,数一数有几根手指?手指之间的空隙我们称为间隔,数一数有几个间隔?3.不仅手指之间有间隔,排队的同学之间也有间隔,路边的大树之间也有间隔,路灯之间也有间隔,隔离墩之间也有间隔。间隔在生活中随处可见,那与我们今天的学习有什么关系呢?带着这个疑问,开启我们今天的学习。
【设计意图:猜谜语导入,引起学生的兴趣,提高学生参与学习的积极性。与孩子们一起做观察手指的活动,让学生在生动活泼的游戏中初步感知与理解“间隔”和“间隔数”,为下面的学习做好铺垫。】
二、初步感知,理解植树问题三种情况。出示情境图。
学校门前有一条长 20米的小路,计划在小路一旁植树,每 5米栽一棵。
1.你能发现哪些数学信息?
2.可以提出什么数学问题?
3.“每隔 5米栽一棵”是什么意思呢?
4.在这条长 20米的小路一旁植树,每隔 5米栽一棵,可以栽多少棵呢?下面,请同学们在学习纸上画一画,数一数,看看可以栽多少棵树。学生活动,画一画。
5. 完成后,跟你的同桌交流一下。
6. 谁能给大家分享一下,你是怎样画的呢?
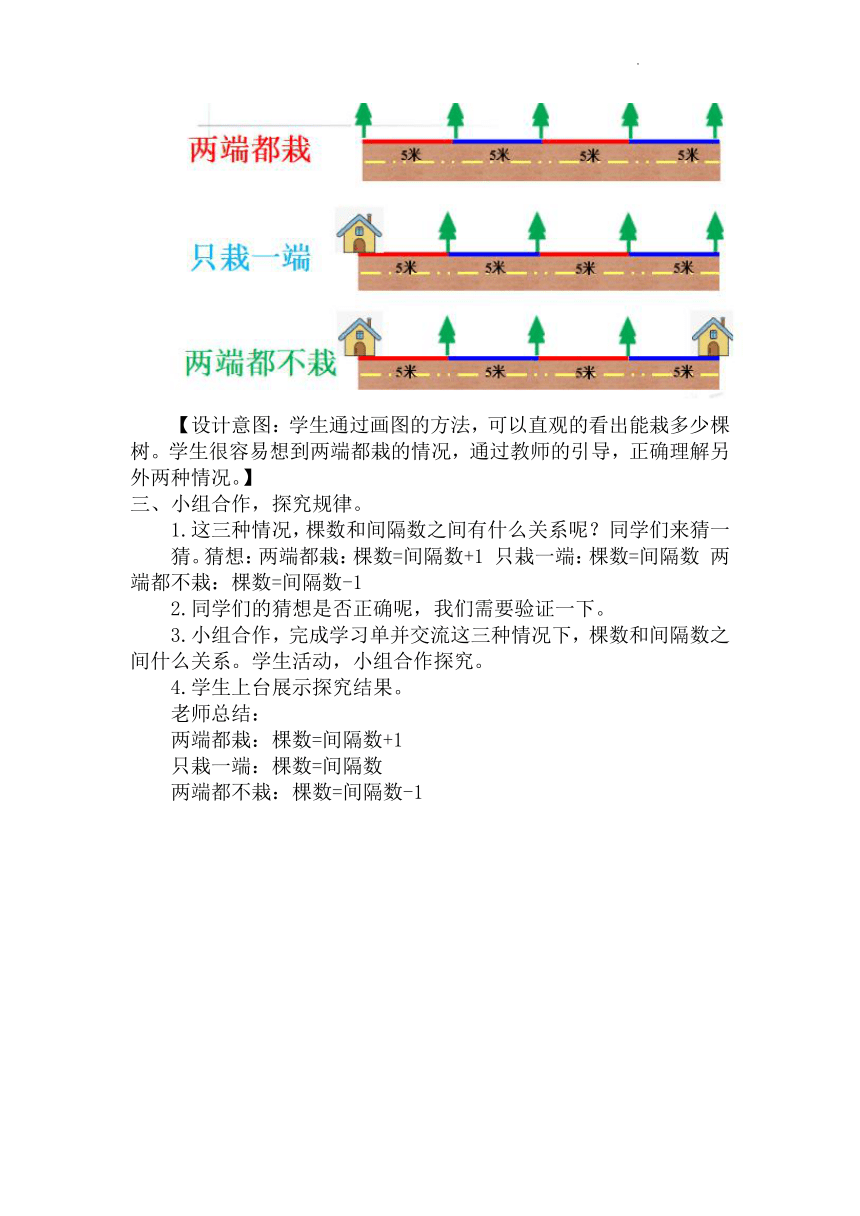
7. 学生上台展示,说一说每种情况栽的棵数和间隔数。老师总结:从小路的一端一直栽到另一端,这种情况称为两端都栽;当小路一端有房子等建筑物时,一端没法栽,另一端可以栽,这种情况称为只栽一端;当小路两端都有建筑物时,两端都没法栽,这种情况称为两端都不栽。
【设计意图:学生通过画图的方法,可以直观的看出能栽多少棵树。学生很容易想到两端都栽的情况,通过教师的引导,正确理解另外两种情况。】
三、小组合作,探究规律。
1.这三种情况,棵数和间隔数之间有什么关系呢?同学们来猜一
猜。猜想:两端都栽:棵数=间隔数+1 只栽一端:棵数=间隔数 两端都不栽:棵数=间隔数-1
2.同学们的猜想是否正确呢,我们需要验证一下。
3.小组合作,完成学习单并交流这三种情况下,棵数和间隔数之间什么关系。学生活动,小组合作探究。
4.学生上台展示探究结果。
老师总结:
两端都栽:棵数=间隔数+1
只栽一端:棵数=间隔数
两端都不栽:棵数=间隔数-1
5.我们也可以借助小手来帮助我们理解。老师带领学生一起用小手验证。
6.三种情况棵数和间隔数之间都有关系,要想求棵数,只要知道间隔数就迎刃而解了。你会列式计算间隔数吗?
20÷5=4(个)
7.你能用计算的方法求三种情况栽树的棵数吗?
两端都栽 20÷5 = 4(个)小路长20米,每隔5米栽一棵树。
4 + 1 = 5(棵)
只栽一端 20÷5 = 4(个)
4个间隔4棵
两端都不栽 20÷5 = 4(个)
4 - 1 = 3(棵)
8.今天我们研究了植树的三种情况。在数学上,与间隔相关的问题,我们统称为植树问题。(出示课题)
【设计意图:学生通过猜想——验证得到了植树问题三种情况的规律。在小组合作的探究过程中,深入理解了植树问题基本规律,建立植树问题的模型,为解决植树问题奠定坚实的基础。】
四、学以致用,解决问题。
生活中的植树问题有很多,我们一起来解决生活中的植树问题吧。1.在一条全长 180米的街道一旁安装路灯(两端都要安装),每隔 6米安一座。一共要安装多少座路灯?
间隔数:180 ÷ 6 = 30(个)
路灯数:30 + 1 = 31(座)
答:一共要安装31 座路灯
2.一件衣服衣长 56厘米,每 8厘米钉一个扣子,需要准备几个扣子?
间隔数:56 ÷ 8 = 7(个)扣子数:7个
答:需要准备7个扣子。
3.把一根木头锯成 5段,每锯断一次需要 6分钟,锯完这根木头一共需要多少分钟?
(先画出示意图,再列式解答。)先让学生说一说每一题中的“小树”是什么,然后再解答。
间隔数:5个锯的次数:5 - 1 = 4(次)
需要时间:6 × 4 = 24(分钟)
答:一共需要24分钟。
【设计意图:通过多层次的练习,使学生进一步理解在不同情境
中棵数与间隔数之间关系,找到规律,更牢固的建立数学模型。同时也进一步培养学生深刻理解题意,仔细计算的好习惯。】
五、回顾总结,巩固提升。
同学们,这节课你有什么收货?这节课我们解决了在小路上植树的问题,在街道上安装路灯的问题,衣服上钉扣子的问题,锯木头问题,这些问题都属于植树问题。生活中的植树问题还有很多很多,只要我们善于发现、勤于思考,我们一定会在数学的王国里获得更多的知识、发现更多的奥秘。
【板书设计】
植树问题
两端都栽:棵数=间隔数+1
只栽一端:棵数=间隔数
两端都不栽:棵数=间隔数-1
《植树问题》教学反思
本节课的学习目的是结合植树的情境,借助生活经验和画图的策略,学习间隔现象中的规律。在让学生经历观察、操作、分析等一系列寻找规律的过程,掌握植树问题的规律,建立植树问题的模型并利用模型解决实际问题。在设计教学时,引导学生自主探究,让学生经历知识形成的全过程,并能从中学到解决问题的思想方法。反思整个教学过程,我认为以下几点做得比较好:
1.主线明确清晰,即从生活中抽取植树现象,从简单问题入手,通过操作、观察、分析、思考,抽象出规律,建立数学模型,再将这一数学模型应用于生活实际。
2.利用几何直观是探究“智慧广场”中规律的重要策略。我在教学时让学生用画图的方法表示自己的想法。在交流的过程,通过展示让学生直观感受到不同情况下植树的棵数与间隔数的关系。在这个基础上,再要求学生借助示意图发现规律,并理解为什么会存在这样的规律。
3.应用拓展,培养数学建模思想。数学建模的目的不仅仅是获得数学结论,更重要的是在建模的过程中促进知识的内化、思想的升华。在经历了“提出猜想——举例验证——完善规律”的过程之后,建立模型就显得尤为重要。在引导学生运用规律解决例题的同时,“植树问题”的模型也成功的构建起来了。然后引导学生拓展模型来解决生活中的实际问题,让学生感受数学的思想方法对解决实际问题的巨大作用,从而增强用模意识。
在本节课中,我也存在着很多不足。
1.对课堂生成的问题处理不够灵活,不能进行很好的利用。
2.教学语言不够精炼,过于啰嗦。
3.整节课大部分时间是老师领着学生去学习,没有完全放手学生去探究,也没有让学生去充分的表达自己的想法。总之,自己今后还要加强学习,不断提高自己的教学水平。
【教学目标】
1.结合植树问题的情境,借助生活经验和画图的策略学习并掌握植树问题的规律。
2.学生在丰富的素材中,经历观察、操作、分析等寻找规律的过程,初步培养学生从实际问题中探索规律,找出解决问题的有效方法的能力。
3.学生在充分的自主探索,合作交流中,增强探究的欲望,体验成功的喜悦,感受数学的魅力。
【教学重点】建立植树问题的模型并掌握其规律。
【教学难点】能根据不同情况选择正确方法解决植树问题。
【教学准备】学习单、板贴。
【教学过程】
一、创设情境,导入新课。
1.同学们,喜欢猜谜语吗?老师给大家带来一个谜语(课件出示):两棵小树十个杈,不长叶子不开花,能写会算还会画,天天干活不说话。
2.请同学们伸出你的左手,分开五指,数一数有几根手指?手指之间的空隙我们称为间隔,数一数有几个间隔?3.不仅手指之间有间隔,排队的同学之间也有间隔,路边的大树之间也有间隔,路灯之间也有间隔,隔离墩之间也有间隔。间隔在生活中随处可见,那与我们今天的学习有什么关系呢?带着这个疑问,开启我们今天的学习。
【设计意图:猜谜语导入,引起学生的兴趣,提高学生参与学习的积极性。与孩子们一起做观察手指的活动,让学生在生动活泼的游戏中初步感知与理解“间隔”和“间隔数”,为下面的学习做好铺垫。】
二、初步感知,理解植树问题三种情况。出示情境图。
学校门前有一条长 20米的小路,计划在小路一旁植树,每 5米栽一棵。
1.你能发现哪些数学信息?
2.可以提出什么数学问题?
3.“每隔 5米栽一棵”是什么意思呢?
4.在这条长 20米的小路一旁植树,每隔 5米栽一棵,可以栽多少棵呢?下面,请同学们在学习纸上画一画,数一数,看看可以栽多少棵树。学生活动,画一画。
5. 完成后,跟你的同桌交流一下。
6. 谁能给大家分享一下,你是怎样画的呢?
7. 学生上台展示,说一说每种情况栽的棵数和间隔数。老师总结:从小路的一端一直栽到另一端,这种情况称为两端都栽;当小路一端有房子等建筑物时,一端没法栽,另一端可以栽,这种情况称为只栽一端;当小路两端都有建筑物时,两端都没法栽,这种情况称为两端都不栽。
【设计意图:学生通过画图的方法,可以直观的看出能栽多少棵树。学生很容易想到两端都栽的情况,通过教师的引导,正确理解另外两种情况。】
三、小组合作,探究规律。
1.这三种情况,棵数和间隔数之间有什么关系呢?同学们来猜一
猜。猜想:两端都栽:棵数=间隔数+1 只栽一端:棵数=间隔数 两端都不栽:棵数=间隔数-1
2.同学们的猜想是否正确呢,我们需要验证一下。
3.小组合作,完成学习单并交流这三种情况下,棵数和间隔数之间什么关系。学生活动,小组合作探究。
4.学生上台展示探究结果。
老师总结:
两端都栽:棵数=间隔数+1
只栽一端:棵数=间隔数
两端都不栽:棵数=间隔数-1
5.我们也可以借助小手来帮助我们理解。老师带领学生一起用小手验证。
6.三种情况棵数和间隔数之间都有关系,要想求棵数,只要知道间隔数就迎刃而解了。你会列式计算间隔数吗?
20÷5=4(个)
7.你能用计算的方法求三种情况栽树的棵数吗?
两端都栽 20÷5 = 4(个)小路长20米,每隔5米栽一棵树。
4 + 1 = 5(棵)
只栽一端 20÷5 = 4(个)
4个间隔4棵
两端都不栽 20÷5 = 4(个)
4 - 1 = 3(棵)
8.今天我们研究了植树的三种情况。在数学上,与间隔相关的问题,我们统称为植树问题。(出示课题)
【设计意图:学生通过猜想——验证得到了植树问题三种情况的规律。在小组合作的探究过程中,深入理解了植树问题基本规律,建立植树问题的模型,为解决植树问题奠定坚实的基础。】
四、学以致用,解决问题。
生活中的植树问题有很多,我们一起来解决生活中的植树问题吧。1.在一条全长 180米的街道一旁安装路灯(两端都要安装),每隔 6米安一座。一共要安装多少座路灯?
间隔数:180 ÷ 6 = 30(个)
路灯数:30 + 1 = 31(座)
答:一共要安装31 座路灯
2.一件衣服衣长 56厘米,每 8厘米钉一个扣子,需要准备几个扣子?
间隔数:56 ÷ 8 = 7(个)扣子数:7个
答:需要准备7个扣子。
3.把一根木头锯成 5段,每锯断一次需要 6分钟,锯完这根木头一共需要多少分钟?
(先画出示意图,再列式解答。)先让学生说一说每一题中的“小树”是什么,然后再解答。
间隔数:5个锯的次数:5 - 1 = 4(次)
需要时间:6 × 4 = 24(分钟)
答:一共需要24分钟。
【设计意图:通过多层次的练习,使学生进一步理解在不同情境
中棵数与间隔数之间关系,找到规律,更牢固的建立数学模型。同时也进一步培养学生深刻理解题意,仔细计算的好习惯。】
五、回顾总结,巩固提升。
同学们,这节课你有什么收货?这节课我们解决了在小路上植树的问题,在街道上安装路灯的问题,衣服上钉扣子的问题,锯木头问题,这些问题都属于植树问题。生活中的植树问题还有很多很多,只要我们善于发现、勤于思考,我们一定会在数学的王国里获得更多的知识、发现更多的奥秘。
【板书设计】
植树问题
两端都栽:棵数=间隔数+1
只栽一端:棵数=间隔数
两端都不栽:棵数=间隔数-1
《植树问题》教学反思
本节课的学习目的是结合植树的情境,借助生活经验和画图的策略,学习间隔现象中的规律。在让学生经历观察、操作、分析等一系列寻找规律的过程,掌握植树问题的规律,建立植树问题的模型并利用模型解决实际问题。在设计教学时,引导学生自主探究,让学生经历知识形成的全过程,并能从中学到解决问题的思想方法。反思整个教学过程,我认为以下几点做得比较好:
1.主线明确清晰,即从生活中抽取植树现象,从简单问题入手,通过操作、观察、分析、思考,抽象出规律,建立数学模型,再将这一数学模型应用于生活实际。
2.利用几何直观是探究“智慧广场”中规律的重要策略。我在教学时让学生用画图的方法表示自己的想法。在交流的过程,通过展示让学生直观感受到不同情况下植树的棵数与间隔数的关系。在这个基础上,再要求学生借助示意图发现规律,并理解为什么会存在这样的规律。
3.应用拓展,培养数学建模思想。数学建模的目的不仅仅是获得数学结论,更重要的是在建模的过程中促进知识的内化、思想的升华。在经历了“提出猜想——举例验证——完善规律”的过程之后,建立模型就显得尤为重要。在引导学生运用规律解决例题的同时,“植树问题”的模型也成功的构建起来了。然后引导学生拓展模型来解决生活中的实际问题,让学生感受数学的思想方法对解决实际问题的巨大作用,从而增强用模意识。
在本节课中,我也存在着很多不足。
1.对课堂生成的问题处理不够灵活,不能进行很好的利用。
2.教学语言不够精炼,过于啰嗦。
3.整节课大部分时间是老师领着学生去学习,没有完全放手学生去探究,也没有让学生去充分的表达自己的想法。总之,自己今后还要加强学习,不断提高自己的教学水平。
