2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.1变化率问题(2)课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.1.1变化率问题(2)课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 319.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
5.1.1 变化率问题(2)
1. 平均速度:
运动员在时间段[t0, t0+Δt]内的平均速度为
当Δt无限趋近于0时,平均速度的极限为瞬时速度,记为
2. 瞬时速度:
复习回顾:
3. 平均变化率:
4. 瞬时变化率:
问题2 抛物线的切线的斜率
我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切. 对于一般的曲线C,如何定义它的切线呢 下面我们以抛物线f(x)=x2为例进行研究.
探究 你认为应该如何定义抛物线f(x)=x2在点P0(1, 1)处的切线
与研究瞬时速度类似,为了研究抛物线f(x)=x2在点P0(1, 1)处的切线,我们通常在点P0(1, 1)的附近任取一点P(x, x2),考察抛物线f(x)=x2的割线P0P的变化情况.
x
y
1
2
1
2
3
4
O
P
P0
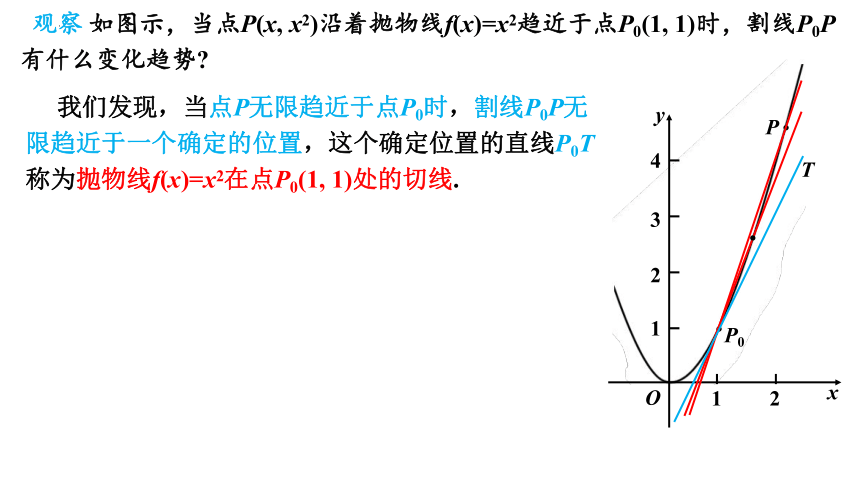
观察 如图示,当点P(x, x2)沿着抛物线f(x)=x2趋近于点P0(1, 1)时,割线P0P有什么变化趋势
T
我们发现,当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为抛物线f(x)=x2在点P0(1, 1)处的切线.
探究 我们知道,斜率是确定直线的一个要素. 如何求抛物线f(x)=x2在点P0(1, 1)处的切线P0T的斜率k0呢
由切线定义可知,抛物线f(x)=x2在点P0(1, 1)处的切线P0T的斜率与割线P0P的斜率有内在联系. 记 x=x-1 ,则点P的坐标是(1+ x, (1+ x)2),于是,割线P0P的斜率为
注: x可以是正值,也可以是负值,但不为0.
x
y
1
2
1
2
3
4
O
P
P0
T
x <0 x >0 x x
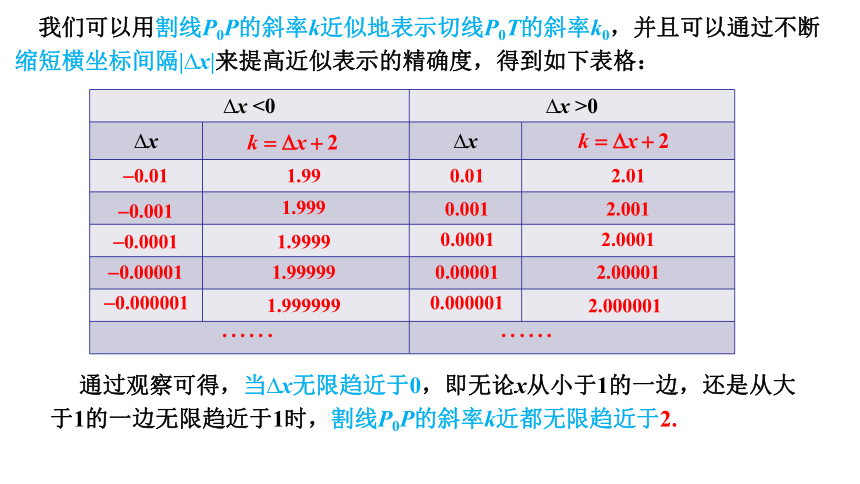
通过观察可得,当 x无限趋近于0,即无论x从小于1的一边,还是从大于1的一边无限趋近于1时,割线P0P的斜率k近都无限趋近于2.
我们可以用割线P0P的斜率k近似地表示切线P0T的斜率k0,并且可以通过不断缩短横坐标间隔| x|来提高近似表示的精确度,得到如下表格:
事实上,由 可以发现,当 x在无限趋近于0时,
无限趋近于2,我们把2叫做“当△x无限趋近于0时, 的极限”,记为
切线的斜率:
也就是说,当点P无限靠近点P0,即 x无限趋近于0时,割线P0P无限趋近于切线P0T,因此切线P0T的斜率为
例1 求抛物线f(x)=x2+2x在点P (1, 3)处切线的斜率.
变式 求抛物线f(x)=x2+2x在点P (1, 3)处的切线方程.
例2 求抛物线f(x)=2x2-1在x=1处的切线方程.
例2 求抛物线f(x)=2x2-1在x=1处的切线方程.
1. 你认为应该怎样定义抛物线f(x)=x2在点(x0, x02)处的切线 试求抛物线f(x)=x2在点(-1, 1)处切线的斜率.
课本P64
2. 求抛物线f(x)=x2+1在点(0, 1)处的切线方程.
课本P64
思考 观察问题1中的函数 的图象,平均速度
的几何意义是什么 瞬时速度v(1)呢
t
h
1
O
(1, h(1))
(1+ t, h(1+ t))
1.高台跳水运动员平均速度及瞬时速度
2.抛物线的割线及切线的斜率
课堂小结:
作业:
教材P70页习题5.1第7题.
1. 求抛物线y=x2-1在点A(2,3)处切线的斜率.
2. 求抛物线y=x2+2x+3在x=1处的切线方程.
教材P105页复习参考题第1题.
5.1.1 变化率问题(2)
1. 平均速度:
运动员在时间段[t0, t0+Δt]内的平均速度为
当Δt无限趋近于0时,平均速度的极限为瞬时速度,记为
2. 瞬时速度:
复习回顾:
3. 平均变化率:
4. 瞬时变化率:
问题2 抛物线的切线的斜率
我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切. 对于一般的曲线C,如何定义它的切线呢 下面我们以抛物线f(x)=x2为例进行研究.
探究 你认为应该如何定义抛物线f(x)=x2在点P0(1, 1)处的切线
与研究瞬时速度类似,为了研究抛物线f(x)=x2在点P0(1, 1)处的切线,我们通常在点P0(1, 1)的附近任取一点P(x, x2),考察抛物线f(x)=x2的割线P0P的变化情况.
x
y
1
2
1
2
3
4
O
P
P0
观察 如图示,当点P(x, x2)沿着抛物线f(x)=x2趋近于点P0(1, 1)时,割线P0P有什么变化趋势
T
我们发现,当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为抛物线f(x)=x2在点P0(1, 1)处的切线.
探究 我们知道,斜率是确定直线的一个要素. 如何求抛物线f(x)=x2在点P0(1, 1)处的切线P0T的斜率k0呢
由切线定义可知,抛物线f(x)=x2在点P0(1, 1)处的切线P0T的斜率与割线P0P的斜率有内在联系. 记 x=x-1 ,则点P的坐标是(1+ x, (1+ x)2),于是,割线P0P的斜率为
注: x可以是正值,也可以是负值,但不为0.
x
y
1
2
1
2
3
4
O
P
P0
T
x <0 x >0 x x
通过观察可得,当 x无限趋近于0,即无论x从小于1的一边,还是从大于1的一边无限趋近于1时,割线P0P的斜率k近都无限趋近于2.
我们可以用割线P0P的斜率k近似地表示切线P0T的斜率k0,并且可以通过不断缩短横坐标间隔| x|来提高近似表示的精确度,得到如下表格:
事实上,由 可以发现,当 x在无限趋近于0时,
无限趋近于2,我们把2叫做“当△x无限趋近于0时, 的极限”,记为
切线的斜率:
也就是说,当点P无限靠近点P0,即 x无限趋近于0时,割线P0P无限趋近于切线P0T,因此切线P0T的斜率为
例1 求抛物线f(x)=x2+2x在点P (1, 3)处切线的斜率.
变式 求抛物线f(x)=x2+2x在点P (1, 3)处的切线方程.
例2 求抛物线f(x)=2x2-1在x=1处的切线方程.
例2 求抛物线f(x)=2x2-1在x=1处的切线方程.
1. 你认为应该怎样定义抛物线f(x)=x2在点(x0, x02)处的切线 试求抛物线f(x)=x2在点(-1, 1)处切线的斜率.
课本P64
2. 求抛物线f(x)=x2+1在点(0, 1)处的切线方程.
课本P64
思考 观察问题1中的函数 的图象,平均速度
的几何意义是什么 瞬时速度v(1)呢
t
h
1
O
(1, h(1))
(1+ t, h(1+ t))
1.高台跳水运动员平均速度及瞬时速度
2.抛物线的割线及切线的斜率
课堂小结:
作业:
教材P70页习题5.1第7题.
1. 求抛物线y=x2-1在点A(2,3)处切线的斜率.
2. 求抛物线y=x2+2x+3在x=1处的切线方程.
教材P105页复习参考题第1题.
