2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.2函数的极值与最大(小)值(2)课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第二册5.3.2函数的极值与最大(小)值(2)课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 438.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 10:34:02 | ||
图片预览





文档简介
(共21张PPT)
5.3.2 函数的极值与最大(小)值(2)
—函数的最大(小)值
1. 求可导函数f(x)极值的步骤:
(2) 求导数f ′(x);
(3) 求方程f ′(x)=0的根;
(4) 把定义域划分为部分区间,并列成表格:
检查f ′(x)在方程根左右的符号:
如果左正右负(左增右减),那么f(x)在这个根处取得极大值;
如果左负右正(左减右增),那么f(x)在这个根处取得极小值.
(1) 确定函数的定义域;
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
2. 对于可导函数,若x0是极值点,则 f '(x0)=0;
反之,若f '(x0)=0,则x0不一定是极值点.
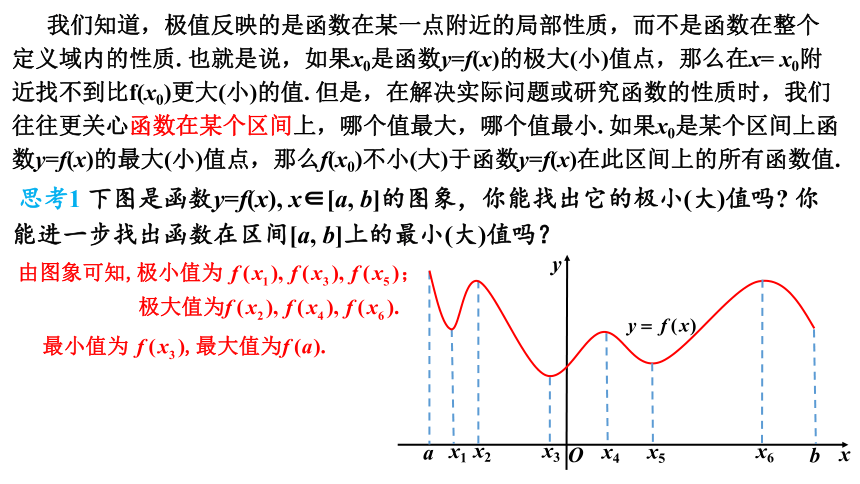
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质. 也就是说,如果x0是函数y=f(x)的极大(小)值点,那么在x= x0附近找不到比f(x0)更大(小)的值. 但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小. 如果x0是某个区间上函数y=f(x)的最大(小)值点,那么f(x0)不小(大)于函数y=f(x)在此区间上的所有函数值.
思考1 下图是函数y=f(x), x∈[a, b]的图象,你能找出它的极小(大)值吗 你能进一步找出函数在区间[a, b]上的最小(大)值吗?
x
y
O
a
b
x1
x2
x3
x4
x5
x6
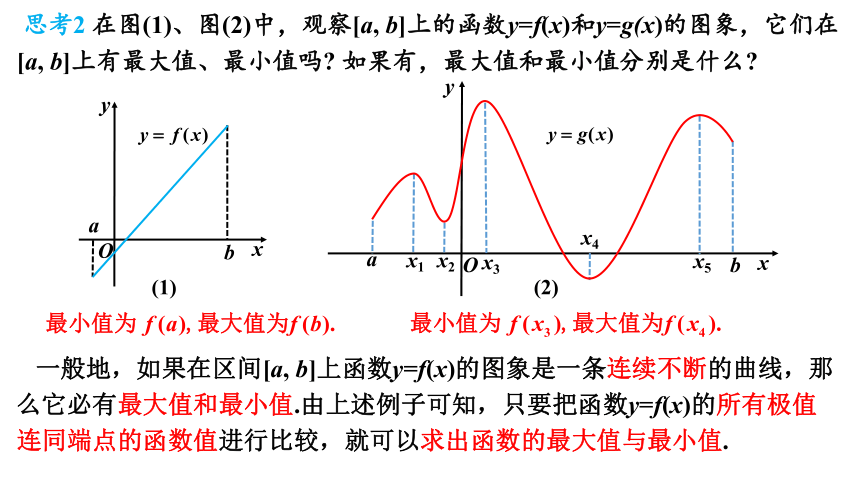
思考2 在图(1)、图(2)中,观察[a, b]上的函数y=f(x)和y=g(x)的图象,它们在[a, b]上有最大值、最小值吗 如果有,最大值和最小值分别是什么
x
y
O
a
b
(1)
(2)
x
y
O
a
b
x1
x2
x3
x4
x5
一般地,如果在区间[a, b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.由上述例子可知,只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.
说明:
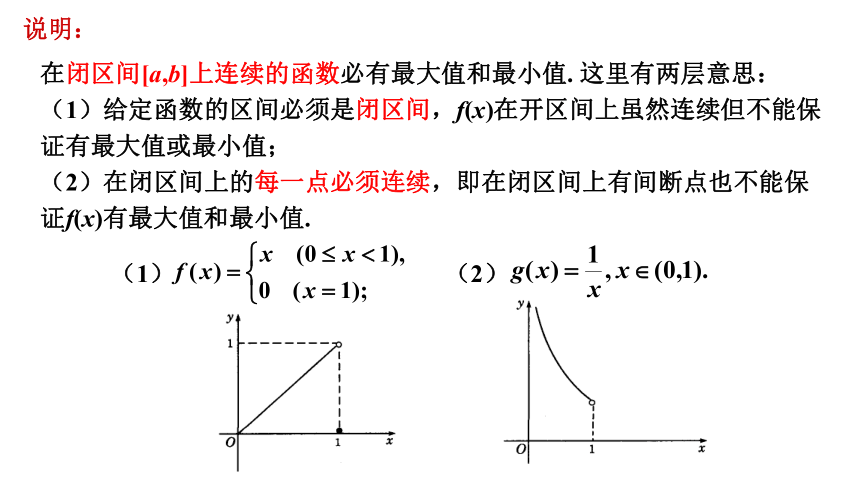
在闭区间[a,b]上连续的函数必有最大值和最小值. 这里有两层意思:
(1)给定函数的区间必须是闭区间,f(x)在开区间上虽然连续但不能保证有最大值或最小值;
(2)在闭区间上的每一点必须连续,即在闭区间上有间断点也不能保证f(x)有最大值和最小值.
(1)
(2)
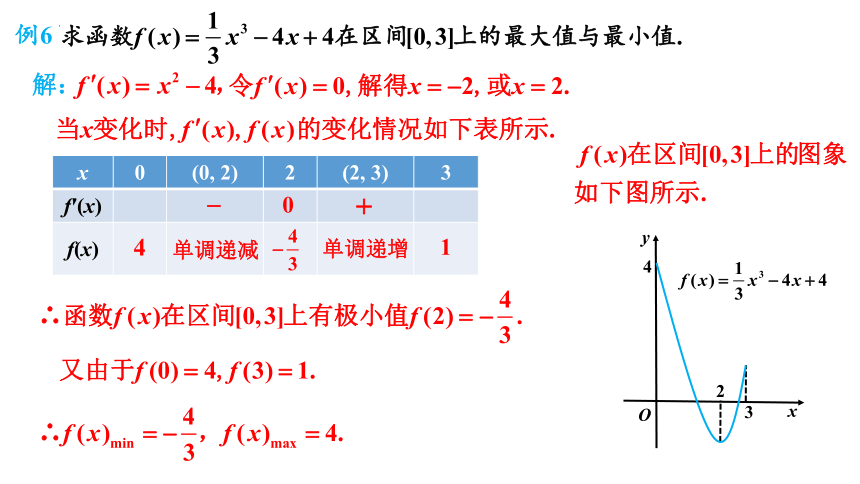
例6
解:
x 0 (0, 2) 2 (2, 3) 3
f′(x)
f(x)
x
y
O
4
2
3
2. 如果函数 f(x)在[a, b]上连续,在(a, b)内可导,那么求 f(x)在[a ,b]内的最大值与最小值的步骤为:
① 求函数f(x)在(a, b)内的极值;
② 求函数f(x)在区间端点处的函数值f(a), f(b);
③ 将函数f(x)在各极值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意区分函数的极值与最值:
函数的极值是函数的局部性质,函数的最值是函数在指定区间上的整体性质.
解:
课本P94
解:
课本P94
解:
课本P94
解:
课本P94
证明:
课本P94
1.利用导数解决与函数相关的问题:
例7
解:
例7
解:
x
y
O
1
-1
-2
例7
解:
x
y
O
1
-1
-2
由例7可见,函数f(x)的图象直观地反映了函数f(x)的性质. 通常,可以按如下步骤画出函数f(x)的大致图象:
(1) 求出函数f(x)的定义域;
(2) 求导数f′(x)及函数f′(x)的零点;
(3) 用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,并得出f(x)的单调性与极值;
(4) 确定f(x)的图象所经过的一些特殊点,以及图象的变化趋势;
(5) 画出f(x)的大致图象.
2.导数在解决实际问题中的应用
问题 饮料瓶大小对饮料公司利润的影响
(1) 你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些 你想从数学上知道它的道理吗
(2) 是不是饮料瓶越大,饮料公司的利润越大
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
解:
证明:
x
y
O
1
π
课本P97
解:
2.如图,用铁丝围成一个上面是半圆,下面是矩形的图形,其面积为a m2.为使所用材料最省,圆的直径应为多少 .
课本P97
小结:
求 f(x)在[a ,b]内的最大值与最小值的步骤为:
1. 求函数f(x)在(a, b)内的极值;
2. 求函数f(x)在区间端点处的函数值f(a), f(b);
3. 将函数f(x)在各极值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
5.3.2 函数的极值与最大(小)值(2)
—函数的最大(小)值
1. 求可导函数f(x)极值的步骤:
(2) 求导数f ′(x);
(3) 求方程f ′(x)=0的根;
(4) 把定义域划分为部分区间,并列成表格:
检查f ′(x)在方程根左右的符号:
如果左正右负(左增右减),那么f(x)在这个根处取得极大值;
如果左负右正(左减右增),那么f(x)在这个根处取得极小值.
(1) 确定函数的定义域;
即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
2. 对于可导函数,若x0是极值点,则 f '(x0)=0;
反之,若f '(x0)=0,则x0不一定是极值点.
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质. 也就是说,如果x0是函数y=f(x)的极大(小)值点,那么在x= x0附近找不到比f(x0)更大(小)的值. 但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小. 如果x0是某个区间上函数y=f(x)的最大(小)值点,那么f(x0)不小(大)于函数y=f(x)在此区间上的所有函数值.
思考1 下图是函数y=f(x), x∈[a, b]的图象,你能找出它的极小(大)值吗 你能进一步找出函数在区间[a, b]上的最小(大)值吗?
x
y
O
a
b
x1
x2
x3
x4
x5
x6
思考2 在图(1)、图(2)中,观察[a, b]上的函数y=f(x)和y=g(x)的图象,它们在[a, b]上有最大值、最小值吗 如果有,最大值和最小值分别是什么
x
y
O
a
b
(1)
(2)
x
y
O
a
b
x1
x2
x3
x4
x5
一般地,如果在区间[a, b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.由上述例子可知,只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.
说明:
在闭区间[a,b]上连续的函数必有最大值和最小值. 这里有两层意思:
(1)给定函数的区间必须是闭区间,f(x)在开区间上虽然连续但不能保证有最大值或最小值;
(2)在闭区间上的每一点必须连续,即在闭区间上有间断点也不能保证f(x)有最大值和最小值.
(1)
(2)
例6
解:
x 0 (0, 2) 2 (2, 3) 3
f′(x)
f(x)
x
y
O
4
2
3
2. 如果函数 f(x)在[a, b]上连续,在(a, b)内可导,那么求 f(x)在[a ,b]内的最大值与最小值的步骤为:
① 求函数f(x)在(a, b)内的极值;
② 求函数f(x)在区间端点处的函数值f(a), f(b);
③ 将函数f(x)在各极值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
注意区分函数的极值与最值:
函数的极值是函数的局部性质,函数的最值是函数在指定区间上的整体性质.
解:
课本P94
解:
课本P94
解:
课本P94
解:
课本P94
证明:
课本P94
1.利用导数解决与函数相关的问题:
例7
解:
例7
解:
x
y
O
1
-1
-2
例7
解:
x
y
O
1
-1
-2
由例7可见,函数f(x)的图象直观地反映了函数f(x)的性质. 通常,可以按如下步骤画出函数f(x)的大致图象:
(1) 求出函数f(x)的定义域;
(2) 求导数f′(x)及函数f′(x)的零点;
(3) 用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,并得出f(x)的单调性与极值;
(4) 确定f(x)的图象所经过的一些特殊点,以及图象的变化趋势;
(5) 画出f(x)的大致图象.
2.导数在解决实际问题中的应用
问题 饮料瓶大小对饮料公司利润的影响
(1) 你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些 你想从数学上知道它的道理吗
(2) 是不是饮料瓶越大,饮料公司的利润越大
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
例8 某制造商制造并出售球形瓶装的某种饮料. 瓶子的制造成本是0.8πr2分,其中r(单位: cm)是瓶子的半径. 已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1) 瓶子半径多大时,能使每瓶饮料的利润最大
(2) 瓶子半径多大时,每瓶饮料的利润最小
解:
证明:
x
y
O
1
π
课本P97
解:
2.如图,用铁丝围成一个上面是半圆,下面是矩形的图形,其面积为a m2.为使所用材料最省,圆的直径应为多少 .
课本P97
小结:
求 f(x)在[a ,b]内的最大值与最小值的步骤为:
1. 求函数f(x)在(a, b)内的极值;
2. 求函数f(x)在区间端点处的函数值f(a), f(b);
3. 将函数f(x)在各极值与f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
