必修二第一章空间几何体单元测试三(附答案)
文档属性
| 名称 | 必修二第一章空间几何体单元测试三(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 342.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-08 20:46:58 | ||
图片预览

文档简介
必修二第一章空间几何体单元测试三(附答案)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
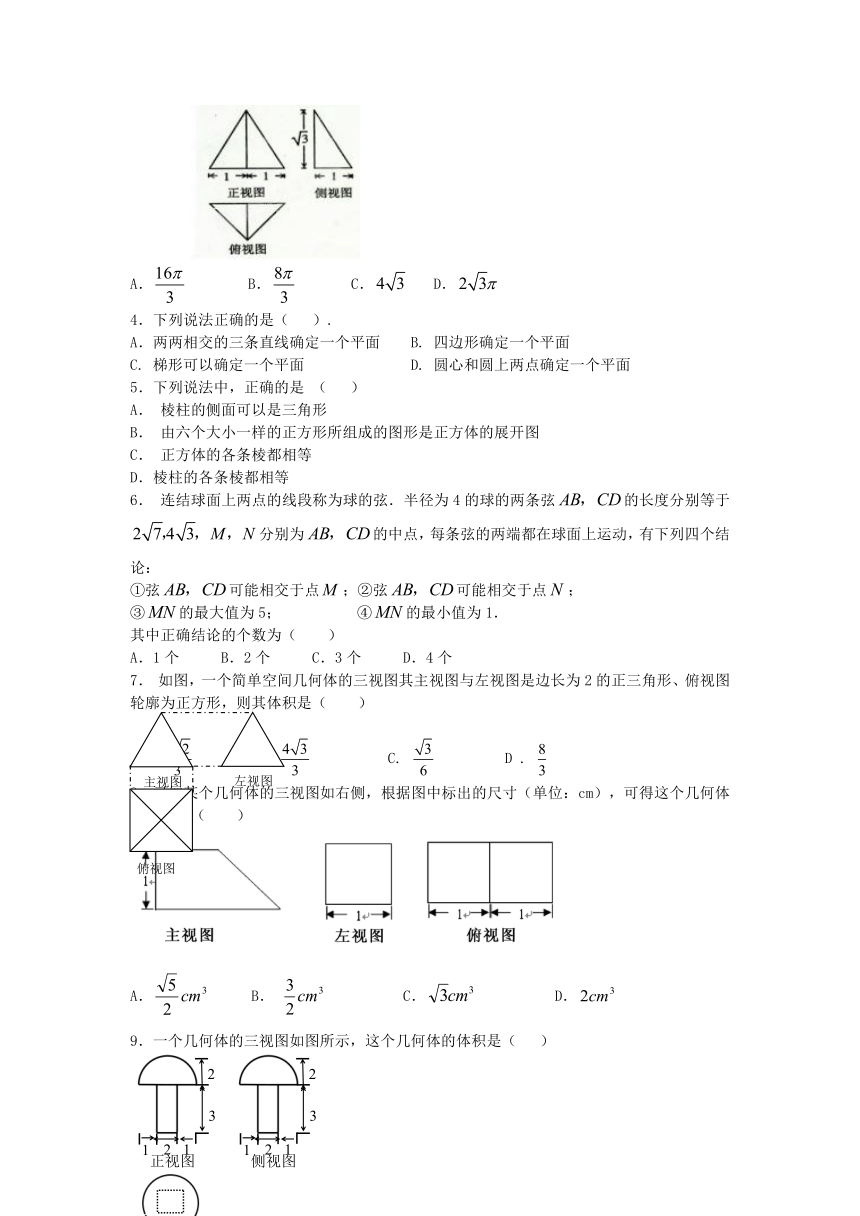
1.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该集合体的俯视图为:( )
2.某几何体的三视图如右图所示,则它的体积是( )
A. B.
C. D.
3.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接
球的表面积为 ( )
A. B. C. D.
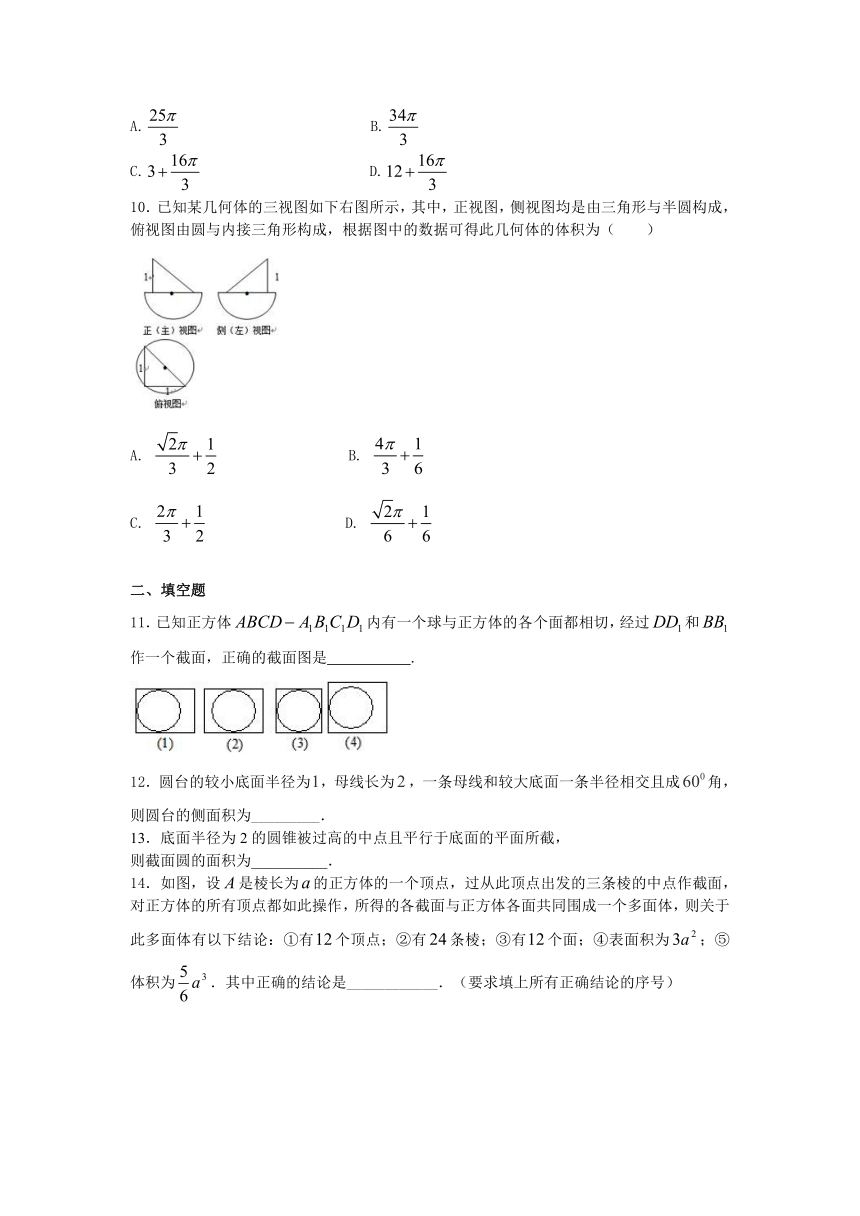
4.下列说法正确的是( ).
A.两两相交的三条直线确定一个平面 B. 四边形确定一个平面
C. 梯形可以确定一个平面 D. 圆心和圆上两点确定一个平面
5.下列说法中,正确的是 ( )
A. 棱柱的侧面可以是三角形
B. 由六个大小一样的正方形所组成的图形是正方体的展开图
C. 正方体的各条棱都相等
D.棱柱的各条棱都相等
6. 连结球面上两点的线段称为球的弦.半径为4的球的两条弦的长度分别等于分别为的中点,每条弦的两端都在球面上运动,有下列四个结论:
①弦可能相交于点;②弦可能相交于点;
③的最大值为5; ④的最小值为1.
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
7. 如图,一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是( )
A. B . C. D .
8.已知某个几何体的三视图如右侧,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. B. C. D.
9.一个几何体的三视图如图所示,这个几何体的体积是( )
A. B.
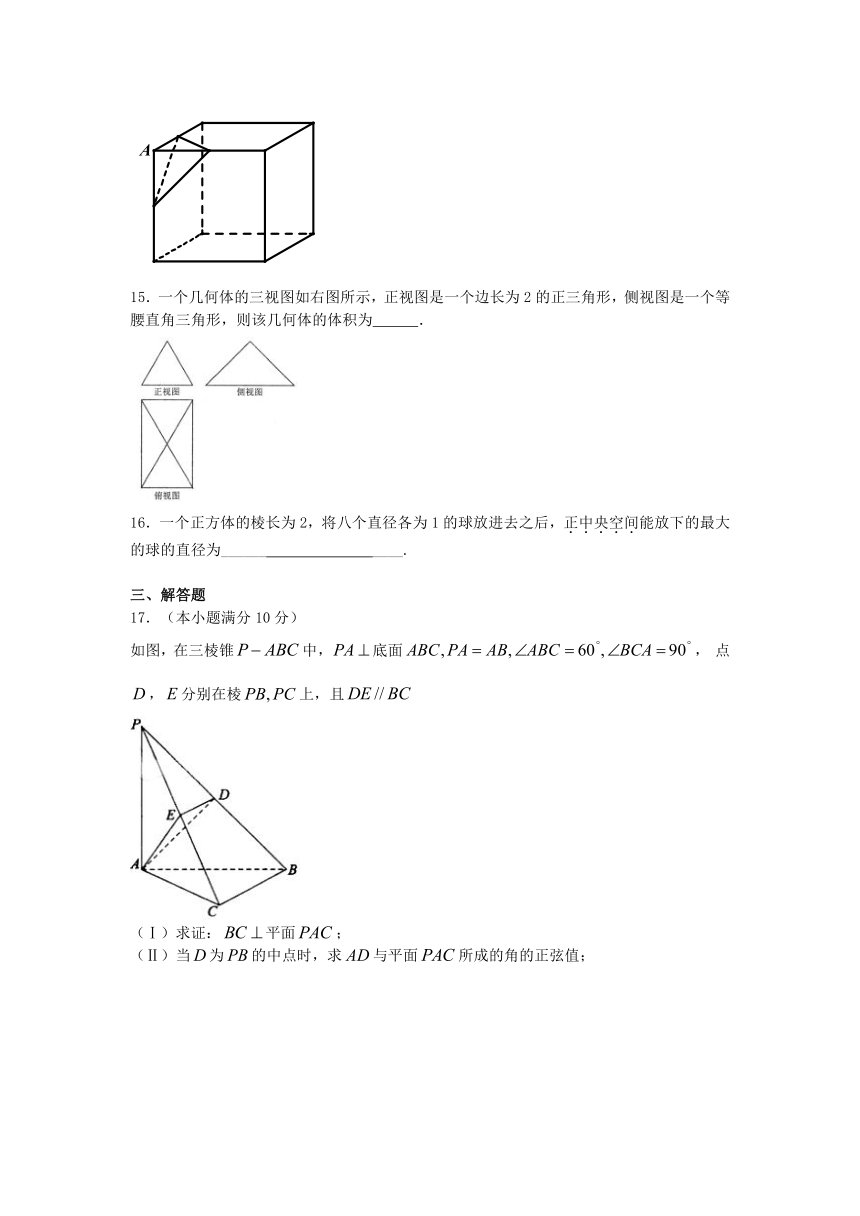
C. D.
10.已知某几何体的三视图如下右图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )
A. B.
C. D.
二、填空题
11.已知正方体内有一个球与正方体的各个面都相切,经过和作一个截面,正确的截面图是 .
12.圆台的较小底面半径为,母线长为,一条母线和较大底面一条半径相交且成角,则圆台的侧面积为_________.
13.底面半径为2的圆锥被过高的中点且平行于底面的平面所截,
则截面圆的面积为__________.
14.如图,设是棱长为的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有个顶点;②有条棱;③有个面;④表面积为;⑤体积为.其中正确的结论是____________.(要求填上所有正确结论的序号)
15.一个几何体的三视图如右图所示,正视图是一个边长为2的正三角形,侧视图是一个等腰直角三角形,则该几何体的体积为 .
16.一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为______ ____.
三、解答题
17.(本小题满分10分)
如图,在三棱锥中,底面, 点,分别在棱上,且
(Ⅰ)求证:平面;
(Ⅱ)当为的中点时,求与平面所成的角的正弦值;
18.如图,直三棱柱中,,,是棱的中点.
(Ⅰ)证明:;
(Ⅱ)求二面角的余弦值。
19.(本小题满分9分)平行四边形ABCD中,AB=2,AD=,且,以BD为折线,把折起,使平面,连AC.
(Ⅰ)求证: (Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅲ)求四面体ABCD外接球的体积.
20.(12分)已知三棱锥各侧棱长均为,三个顶角均为,M,N分别为PA,PC上的点,求周长的最小值.
21.(本题6分)如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心.
(Ⅰ)求圆锥的表面积;
(Ⅱ)经过圆锥的高AO的中点O(作平行于圆锥底面的截面,求截得的圆台的体积.
22.(本小题满分9分)
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=.
(1)求四棱锥S-ABCD的体积.
(2)求证:面SAB⊥面SBC.
(3)求SC与底面ABCD所成角的正切值.
23.如图,直二面角A—BD—C,平面ABD⊥平面BCD,若其中给定 AB=AD =2,,,BC⊥CD .
(Ⅰ)求AC与平面BCD所成的角;
(Ⅱ)求点A到BC的距离.
24.(本小题满分12分)如图,已知四棱锥中,底面是直角梯形,,
,,,平面,.
(Ⅰ)求证:平面;
(Ⅱ)求证:平面;
(Ⅲ)若是的中点,求三棱锥的体积.
25.如图1, E, F,G分别是边长为2的正方形所ABCD所在边的中点,沿EF将ΔCEF截去后,又沿EG将多边形ABEFD折起,使得平面DGEF丄平面ABEG得到如图2所示的多面体.
(1) 求证:FG丄平面BEF;
(2) 求二面角A-BF-E的大小;
(3) 求多面体ADG—BFE的体积.
参考答案
1.C
2.A
3.A
4.C
5.C
6.C
7.B
8.B
9.D
10.D
11.(2)
12.
13.π
14.①②⑤
15.4
16.
17.(Ⅰ)略;(Ⅱ)与平面所成的角的正弦值为。
18.(Ⅰ)证明略
(Ⅱ)二面角的余弦值为
19.(1)略;(2)二面角B-AC-D的大小是;(3) .
20.6
21.(Ⅰ)S表面=(r2+(rl=3(;(Ⅱ).
22.证明:(1) VS-ABCD=××1= ;(2)略;(3)tan∠SCA===。
23..(1)
24.(Ⅰ)略(Ⅱ)略(Ⅲ)
25.(1)略 (2)(3).
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该集合体的俯视图为:( )
2.某几何体的三视图如右图所示,则它的体积是( )
A. B.
C. D.
3.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接
球的表面积为 ( )
A. B. C. D.
4.下列说法正确的是( ).
A.两两相交的三条直线确定一个平面 B. 四边形确定一个平面
C. 梯形可以确定一个平面 D. 圆心和圆上两点确定一个平面
5.下列说法中,正确的是 ( )
A. 棱柱的侧面可以是三角形
B. 由六个大小一样的正方形所组成的图形是正方体的展开图
C. 正方体的各条棱都相等
D.棱柱的各条棱都相等
6. 连结球面上两点的线段称为球的弦.半径为4的球的两条弦的长度分别等于分别为的中点,每条弦的两端都在球面上运动,有下列四个结论:
①弦可能相交于点;②弦可能相交于点;
③的最大值为5; ④的最小值为1.
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
7. 如图,一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是( )
A. B . C. D .
8.已知某个几何体的三视图如右侧,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. B. C. D.
9.一个几何体的三视图如图所示,这个几何体的体积是( )
A. B.
C. D.
10.已知某几何体的三视图如下右图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )
A. B.
C. D.
二、填空题
11.已知正方体内有一个球与正方体的各个面都相切,经过和作一个截面,正确的截面图是 .
12.圆台的较小底面半径为,母线长为,一条母线和较大底面一条半径相交且成角,则圆台的侧面积为_________.
13.底面半径为2的圆锥被过高的中点且平行于底面的平面所截,
则截面圆的面积为__________.
14.如图,设是棱长为的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有个顶点;②有条棱;③有个面;④表面积为;⑤体积为.其中正确的结论是____________.(要求填上所有正确结论的序号)
15.一个几何体的三视图如右图所示,正视图是一个边长为2的正三角形,侧视图是一个等腰直角三角形,则该几何体的体积为 .
16.一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为______ ____.
三、解答题
17.(本小题满分10分)
如图,在三棱锥中,底面, 点,分别在棱上,且
(Ⅰ)求证:平面;
(Ⅱ)当为的中点时,求与平面所成的角的正弦值;
18.如图,直三棱柱中,,,是棱的中点.
(Ⅰ)证明:;
(Ⅱ)求二面角的余弦值。
19.(本小题满分9分)平行四边形ABCD中,AB=2,AD=,且,以BD为折线,把折起,使平面,连AC.
(Ⅰ)求证: (Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅲ)求四面体ABCD外接球的体积.
20.(12分)已知三棱锥各侧棱长均为,三个顶角均为,M,N分别为PA,PC上的点,求周长的最小值.
21.(本题6分)如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心.
(Ⅰ)求圆锥的表面积;
(Ⅱ)经过圆锥的高AO的中点O(作平行于圆锥底面的截面,求截得的圆台的体积.
22.(本小题满分9分)
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=.
(1)求四棱锥S-ABCD的体积.
(2)求证:面SAB⊥面SBC.
(3)求SC与底面ABCD所成角的正切值.
23.如图,直二面角A—BD—C,平面ABD⊥平面BCD,若其中给定 AB=AD =2,,,BC⊥CD .
(Ⅰ)求AC与平面BCD所成的角;
(Ⅱ)求点A到BC的距离.
24.(本小题满分12分)如图,已知四棱锥中,底面是直角梯形,,
,,,平面,.
(Ⅰ)求证:平面;
(Ⅱ)求证:平面;
(Ⅲ)若是的中点,求三棱锥的体积.
25.如图1, E, F,G分别是边长为2的正方形所ABCD所在边的中点,沿EF将ΔCEF截去后,又沿EG将多边形ABEFD折起,使得平面DGEF丄平面ABEG得到如图2所示的多面体.
(1) 求证:FG丄平面BEF;
(2) 求二面角A-BF-E的大小;
(3) 求多面体ADG—BFE的体积.
参考答案
1.C
2.A
3.A
4.C
5.C
6.C
7.B
8.B
9.D
10.D
11.(2)
12.
13.π
14.①②⑤
15.4
16.
17.(Ⅰ)略;(Ⅱ)与平面所成的角的正弦值为。
18.(Ⅰ)证明略
(Ⅱ)二面角的余弦值为
19.(1)略;(2)二面角B-AC-D的大小是;(3) .
20.6
21.(Ⅰ)S表面=(r2+(rl=3(;(Ⅱ).
22.证明:(1) VS-ABCD=××1= ;(2)略;(3)tan∠SCA===。
23..(1)
24.(Ⅰ)略(Ⅱ)略(Ⅲ)
25.(1)略 (2)(3).
