人教版数学七年级下册 10.6 第十章数据的收集、整理与描述 中考新动向 课件(共15张PPT)
文档属性
| 名称 | 人教版数学七年级下册 10.6 第十章数据的收集、整理与描述 中考新动向 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 479.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 09:34:12 | ||
图片预览




文档简介
(共15张PPT)
单元复习课
专题二 中考新动向
【考情讲述】
往届的广东省统计类中考,一般是频数分布表、扇形统计图、条形统计图三者中取二者与中位数、众数、概率等知识结合成综合题,难度略大,一般放在解答题(二)位置;2020与2021年的数学命题,将国家经济与传统文化发展中的热点问题相结合,提炼出具有新时代气息的数学问题,强调了信息与课程内容的整合,注重了实效,树立了学生数据分析观念,让数学更好地服务于生活.近两年的统计题变化趋势:知识单一,降低了难度,均放在解答题(一).
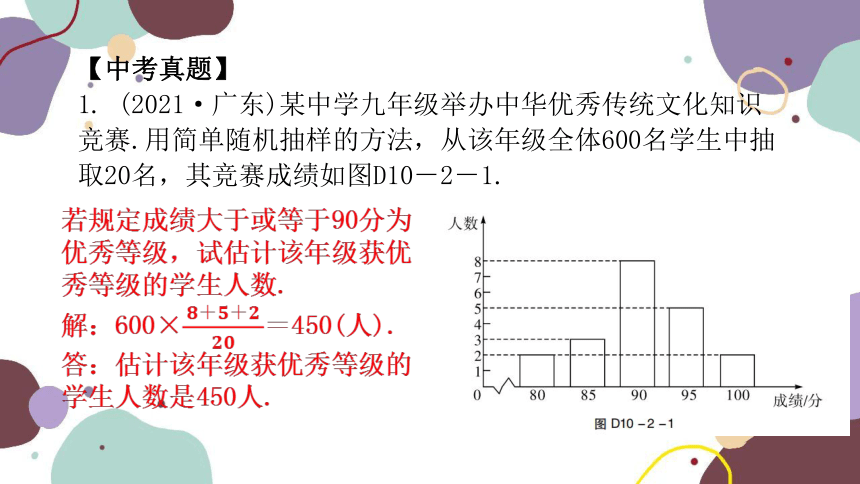
【中考真题】
1. (2021·广东)某中学九年级举办中华优秀传统文化知识竞赛.用简单随机抽样的方法,从该年级全体600名学生中抽取20名,其竞赛成绩如图D10-2-1.
2. (2020·广东)某中学开展主题为“垃圾分类知多少”的调查活动,调查问卷设置了“非常了解”“比较了解”“基本了解”“不太了解”四个等级,要求每名学生选且只能选其中一个等级,随机抽取了120名学生的有效问卷,数据整理如下:
等级 非常了解 比较了解 基本了解 不太了解
人数 24 72 18 x
(1)求x的值;
(2)若该校有学生1 800人,请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人?
解:(1)x=120-(24+72+18)=6.
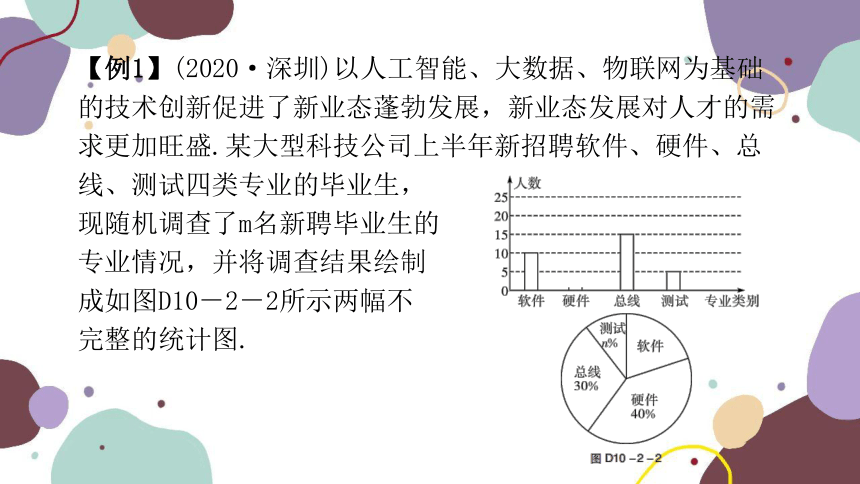
【例1】(2020·深圳)以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,
现随机调查了m名新聘毕业生的
专业情况,并将调查结果绘制
成如图D10-2-2所示两幅不
完整的统计图.
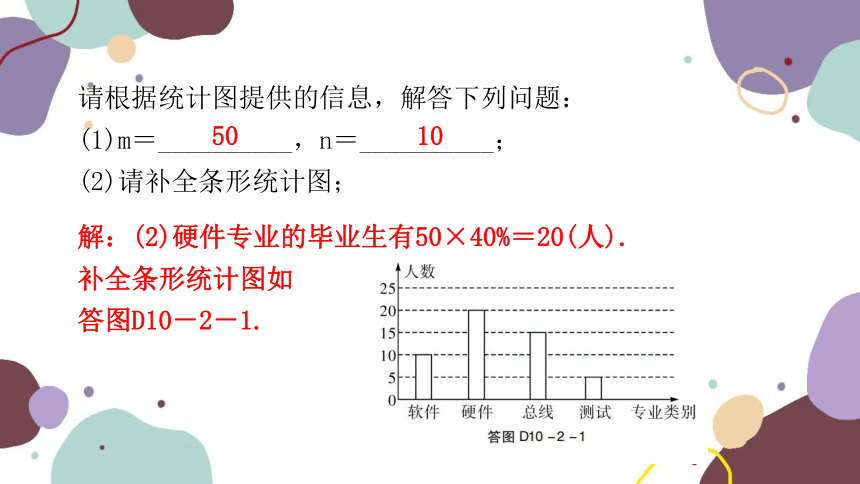
请根据统计图提供的信息,解答下列问题:
(1)m=__________,n=__________;
(2)请补全条形统计图;
50
10
解:(2)硬件专业的毕业生有50×40%=20(人).
补全条形统计图如
答图D10-2-1.
(3)在扇形统计图中,“软件”所对应的扇形的圆心角是__________°;
(4)若该公司新招聘600名毕业生,请你估计“总线”专业的毕业生有__________名.
72
180
1. (创新题)市环保部门为了解城区某一天18时噪声污染情况,随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计,把所抽取的测量数据分成A,B,C,D,E五组,并将统计结果绘制成如图D10-2-3所示的两幅不完整的统计图表.
组别 噪声声级x/dB 频数
A 55≤x<60 4
B 60≤x<65 10
C 65≤x<70 m
D 70≤x<75 8
E 75≤x<80 n
请解答下列问题:
(1)m=__________,n=__________;
(2)在扇形统计图中D组对应的扇形圆心角的度数是__________°;
(3)若该市城区共有400个噪声测量点,请估计该市城区这一天18时噪声声级低于70 dB的测量点的个数.
12
6
72
【例2】(2021·深圳)随机调查某城市30天空气质量指数(AQI),绘制成如图D10-2-4所示的频数分布表和扇形统计图.
空气质量等级 空气质量指数(AQI) 频数
优 AQI≤50 m
良 50<AQI≤100 15
中 100<AQI≤150 9
差 AQI>150 n
(1)m=__________,n=__________;
4
2
(2)求良的占比;
(3)求差的圆心角;
(4)估测该城市一年(以365天计)中大约有__________天AQI为中.
110
2. (2021·广州)某中学为了解九年级学生参加志愿者活动的次数,随机调查了该年级20名学生,统计得到该20名学生参加志愿者活动的次数如下:
3,5,3,6,3,4,4,5,2,4,5,6,1,3,5,
5,4,4,2,4
根据以上数据,得到如下不完整的频数分布表:
(1)表格中的a=__________,b=__________;
次数 1 2 3 4 5 6
人数 1 2 a 6 b 2
4
5
(2)若该校九年级共有300名学生,根据调查统计结果,估计该校九年级学生参加志愿者活动的次数为4次的人数.
谢 谢
单元复习课
专题二 中考新动向
【考情讲述】
往届的广东省统计类中考,一般是频数分布表、扇形统计图、条形统计图三者中取二者与中位数、众数、概率等知识结合成综合题,难度略大,一般放在解答题(二)位置;2020与2021年的数学命题,将国家经济与传统文化发展中的热点问题相结合,提炼出具有新时代气息的数学问题,强调了信息与课程内容的整合,注重了实效,树立了学生数据分析观念,让数学更好地服务于生活.近两年的统计题变化趋势:知识单一,降低了难度,均放在解答题(一).
【中考真题】
1. (2021·广东)某中学九年级举办中华优秀传统文化知识竞赛.用简单随机抽样的方法,从该年级全体600名学生中抽取20名,其竞赛成绩如图D10-2-1.
2. (2020·广东)某中学开展主题为“垃圾分类知多少”的调查活动,调查问卷设置了“非常了解”“比较了解”“基本了解”“不太了解”四个等级,要求每名学生选且只能选其中一个等级,随机抽取了120名学生的有效问卷,数据整理如下:
等级 非常了解 比较了解 基本了解 不太了解
人数 24 72 18 x
(1)求x的值;
(2)若该校有学生1 800人,请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人?
解:(1)x=120-(24+72+18)=6.
【例1】(2020·深圳)以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展,新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生,
现随机调查了m名新聘毕业生的
专业情况,并将调查结果绘制
成如图D10-2-2所示两幅不
完整的统计图.
请根据统计图提供的信息,解答下列问题:
(1)m=__________,n=__________;
(2)请补全条形统计图;
50
10
解:(2)硬件专业的毕业生有50×40%=20(人).
补全条形统计图如
答图D10-2-1.
(3)在扇形统计图中,“软件”所对应的扇形的圆心角是__________°;
(4)若该公司新招聘600名毕业生,请你估计“总线”专业的毕业生有__________名.
72
180
1. (创新题)市环保部门为了解城区某一天18时噪声污染情况,随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计,把所抽取的测量数据分成A,B,C,D,E五组,并将统计结果绘制成如图D10-2-3所示的两幅不完整的统计图表.
组别 噪声声级x/dB 频数
A 55≤x<60 4
B 60≤x<65 10
C 65≤x<70 m
D 70≤x<75 8
E 75≤x<80 n
请解答下列问题:
(1)m=__________,n=__________;
(2)在扇形统计图中D组对应的扇形圆心角的度数是__________°;
(3)若该市城区共有400个噪声测量点,请估计该市城区这一天18时噪声声级低于70 dB的测量点的个数.
12
6
72
【例2】(2021·深圳)随机调查某城市30天空气质量指数(AQI),绘制成如图D10-2-4所示的频数分布表和扇形统计图.
空气质量等级 空气质量指数(AQI) 频数
优 AQI≤50 m
良 50<AQI≤100 15
中 100<AQI≤150 9
差 AQI>150 n
(1)m=__________,n=__________;
4
2
(2)求良的占比;
(3)求差的圆心角;
(4)估测该城市一年(以365天计)中大约有__________天AQI为中.
110
2. (2021·广州)某中学为了解九年级学生参加志愿者活动的次数,随机调查了该年级20名学生,统计得到该20名学生参加志愿者活动的次数如下:
3,5,3,6,3,4,4,5,2,4,5,6,1,3,5,
5,4,4,2,4
根据以上数据,得到如下不完整的频数分布表:
(1)表格中的a=__________,b=__________;
次数 1 2 3 4 5 6
人数 1 2 a 6 b 2
4
5
(2)若该校九年级共有300名学生,根据调查统计结果,估计该校九年级学生参加志愿者活动的次数为4次的人数.
谢 谢
