人教版数学九年级下册 27. 2.2相似三角形应用举例 2课时 教案(表格式)
文档属性
| 名称 | 人教版数学九年级下册 27. 2.2相似三角形应用举例 2课时 教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 85.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 07:36:59 | ||
图片预览

文档简介
上课时间 年 月 日(第 周 星期 ) 总第 课时
备课人 授课班级 九( )班
教学内容 27.2.3. 相似三角形应用举例(1)
教学目标 知识与技能:1、进一步巩固相似三角形的知识. 2、能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题)等的一些实际问题。
过程与方法:通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力。
情感态度与价值观:在运用数学表述和解决问题的过程中,认识数学具有抽象、严谨和应用广泛的特点,体会数学的价值。
教学重点 运用三角形相似的知识计算不能直接测量物体的长度和高度。
教学难点 灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题)。
媒体应用
教学流程 师生活动 设计意图
活动一问题导入 在古希腊,有一位伟大的科学家叫泰勒斯。一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”,这在当时条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗?
活动二例题分析 例1(教材P39例4——测量金字塔高度问题)解:略(见教材P39)例2(教材P40例5 ——测量河宽问题)解:略(见教材P40)问:你还可以用什么方法来测量河的宽度?解法二:如图构造相似三角形。测得BD=120 m,DC=60 m,EC=50 m,求河宽AB。
活动三课堂练习 教材P41练习1、2
活动四归纳与小结 本节课你得到了什么收获?
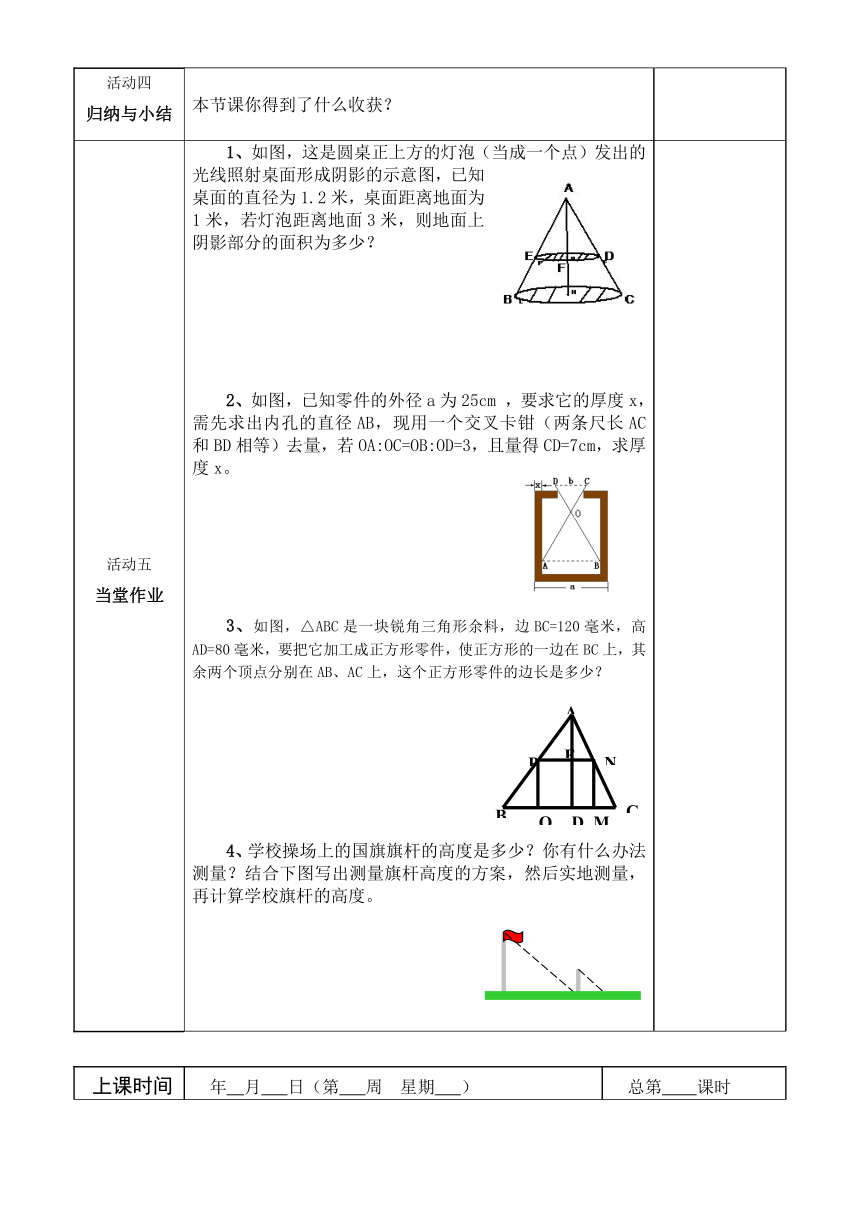
活动五当堂作业 1、如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?2、如图,已知零件的外径a为25cm ,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=3,且量得CD=7cm,求厚度x。3、如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?4、学校操场上的国旗旗杆的高度是多少?你有什么办法测量?结合下图写出测量旗杆高度的方案,然后实地测量,再计算学校旗杆的高度。
上课时间 年 月 日(第 周 星期 ) 总第 课时
备课人 授课班级 九( )班
教学内容 27.2.3. 相似三角形应用举例(2)
教学目标 知识与技能:1、进一步巩固相似三角形的知识. 2、能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题)等的一些实际问题。
过程与方法:通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力。
情感态度与价值观:在运用数学表述和解决问题的过程中,认识数学具有抽象、严谨和应用广泛的特点,体会数学的价值。
教学重点 运用三角形相似的知识计算不能直接测量物体的长度和高度。
教学难点 灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题)。
媒体应用
教学流程 师生活动 设计意图
活动一知识链接 1、判断两三角形相似有哪些方法 2、相似三角形有什么性质?
活动二探索新知 1、阅读课本P40例题6:认真体会这一生活实际中常见的场景,借助图形把这一实际中常见的场景抽象成数学图形,利用相似的性质解决这一实际问题。2、(补充)如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB ∥PQ.建筑物DE的一端所在的直线MN垂直AB于点M,交PC于点N.小亮从胜利街的A处,沿AB着方向前进,小明一直站在P点的位置等候小亮.(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);(2)已知:MN=20cm,MD=8cm,PN=24cm,求(1)中的C点到胜利街口的距离CM.
活动三课堂练习 小明想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
活动四当堂检测 1、如图:小明想测量一颗大树AB的高度,发现树的影子恰好落在土坡的坡面CD和地面CB上,测得CD=4m,BC=10m,CD与地面成30度角,且测得1米竹杆的影子长为2米,那么树的高度是多少?2 、如图,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E,F在BC上,AD交HG于点M,此时有AM/AD=HG/BC(1)设矩形EFGH的长HG=y,宽HE=x,确定y与x的函数关系式;(2)当x为何值时,矩形EFGH的面积S最大 3、如图, △ABC中,AB=6,BC=4,AC=3,点P在BC上运动,过P点作∠DPB=∠A,PD交AB于D,设PB=x,AD=y。(1)求y关于x的函数关系式和x的取值范围。(2)当x取何值时,y最小,最小值是多少
活动五归纳与小结 本节课你得到了什么收获?
活动六教学反思
N
M
Q
P
E
D
C
B
A
备课人 授课班级 九( )班
教学内容 27.2.3. 相似三角形应用举例(1)
教学目标 知识与技能:1、进一步巩固相似三角形的知识. 2、能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题)等的一些实际问题。
过程与方法:通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力。
情感态度与价值观:在运用数学表述和解决问题的过程中,认识数学具有抽象、严谨和应用广泛的特点,体会数学的价值。
教学重点 运用三角形相似的知识计算不能直接测量物体的长度和高度。
教学难点 灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题)。
媒体应用
教学流程 师生活动 设计意图
活动一问题导入 在古希腊,有一位伟大的科学家叫泰勒斯。一天,希腊国王阿马西斯对他说:“听说你什么都知道,那就请你测量一下埃及金字塔的高度吧!”,这在当时条件下是个大难题,因为是很难爬到塔顶的.你知道泰勒斯是怎样测量大金字塔的高度的吗?
活动二例题分析 例1(教材P39例4——测量金字塔高度问题)解:略(见教材P39)例2(教材P40例5 ——测量河宽问题)解:略(见教材P40)问:你还可以用什么方法来测量河的宽度?解法二:如图构造相似三角形。测得BD=120 m,DC=60 m,EC=50 m,求河宽AB。
活动三课堂练习 教材P41练习1、2
活动四归纳与小结 本节课你得到了什么收获?
活动五当堂作业 1、如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?2、如图,已知零件的外径a为25cm ,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=3,且量得CD=7cm,求厚度x。3、如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?4、学校操场上的国旗旗杆的高度是多少?你有什么办法测量?结合下图写出测量旗杆高度的方案,然后实地测量,再计算学校旗杆的高度。
上课时间 年 月 日(第 周 星期 ) 总第 课时
备课人 授课班级 九( )班
教学内容 27.2.3. 相似三角形应用举例(2)
教学目标 知识与技能:1、进一步巩固相似三角形的知识. 2、能够运用三角形相似的知识,解决不能直接测量物体的长度和高度(如测量金字塔高度问题、测量河宽问题)等的一些实际问题。
过程与方法:通过把实际问题转化成有关相似三角形的数学模型,进一步了解数学建模的思想,培养分析问题、解决问题的能力。
情感态度与价值观:在运用数学表述和解决问题的过程中,认识数学具有抽象、严谨和应用广泛的特点,体会数学的价值。
教学重点 运用三角形相似的知识计算不能直接测量物体的长度和高度。
教学难点 灵活运用三角形相似的知识解决实际问题(如何把实际问题抽象为数学问题)。
媒体应用
教学流程 师生活动 设计意图
活动一知识链接 1、判断两三角形相似有哪些方法 2、相似三角形有什么性质?
活动二探索新知 1、阅读课本P40例题6:认真体会这一生活实际中常见的场景,借助图形把这一实际中常见的场景抽象成数学图形,利用相似的性质解决这一实际问题。2、(补充)如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB ∥PQ.建筑物DE的一端所在的直线MN垂直AB于点M,交PC于点N.小亮从胜利街的A处,沿AB着方向前进,小明一直站在P点的位置等候小亮.(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);(2)已知:MN=20cm,MD=8cm,PN=24cm,求(1)中的C点到胜利街口的距离CM.
活动三课堂练习 小明想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得的树高是多少?
活动四当堂检测 1、如图:小明想测量一颗大树AB的高度,发现树的影子恰好落在土坡的坡面CD和地面CB上,测得CD=4m,BC=10m,CD与地面成30度角,且测得1米竹杆的影子长为2米,那么树的高度是多少?2 、如图,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E,F在BC上,AD交HG于点M,此时有AM/AD=HG/BC(1)设矩形EFGH的长HG=y,宽HE=x,确定y与x的函数关系式;(2)当x为何值时,矩形EFGH的面积S最大 3、如图, △ABC中,AB=6,BC=4,AC=3,点P在BC上运动,过P点作∠DPB=∠A,PD交AB于D,设PB=x,AD=y。(1)求y关于x的函数关系式和x的取值范围。(2)当x取何值时,y最小,最小值是多少
活动五归纳与小结 本节课你得到了什么收获?
活动六教学反思
N
M
Q
P
E
D
C
B
A
