2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2排列组合的综合应用(排队问题)课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2排列组合的综合应用(排队问题)课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 15:01:46 | ||
图片预览








文档简介
(共28张PPT)
排列组合的综合应用
(排队问题)
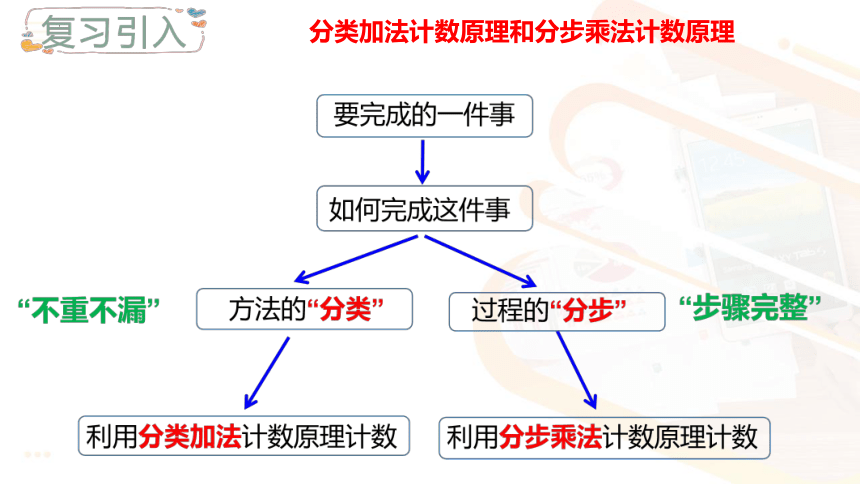
分类加法计数原理和分步乘法计数原理
例1.有7名学生,在下列不同条件下,求不同的排列方法总数.
(1)其中男甲排在正中间;
(2)其中男甲不在排头,也不在排尾;
排队问题
有特殊元素或特殊位置的排列组合问题,通常是先排特殊元素或特殊位置,称为优先法;
特殊元素——优先法
排队问题
例2: 有7名学生,在下列不同条件下,求不同的排列方法总数.
(1)7人排成一排,多少种不同的排法?
(2)7人成两排,第一排3人,第二排4人,多少种不同的排法?
(3)7人成三排,第一排1人,第二排2人,第三排4人,多少种不同的排法?
(4)7人成四排,第一排1人,第二排2人,第三排3人,第四排1人,多少种不同的排法?
将元素进行多行排列与元素进行单行排列的本质是一样的,可以用单行排列的方法数来求解,称为多排问题单排法;
多排问题——单排法
排队问题
例3:有3名女生、4名男生,在下列不同条件下,求不同的排列方法总数.
(1)若三个女生要站在一起,有多少种不同的排法?
(2)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
(3)若三个女生互不相邻,有多少种不同的排法?
(4)男生、女生相间排列,有多少种不同的排法?
(1)若三个女生要站在一起,有多少种不同的排法?
元素相邻问题利用“捆绑法”处理,即把相邻元素看作一个整体,视为一个元素,参与其他元素的排列.同时,应注意捆绑元素的内部排列(也就是要记得给他们“松绑”).
相邻问题——捆绑法
(2)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
练习:3名男生和2名女生排成一队照相,要求女生相邻,共有__________种排法.
(3)若三个女生互不相邻,有多少种不同的排法?
插空法
元素不相邻问题利用“插空法”处理,即先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空档中.有多少个空档要根据具体的题目要求来分析。
不相邻问题——插空法
(4)男生、女生相间排列,有多少种不同的排法?
练习:甲 乙 丙三人相约去看电影,他们的座位恰好是同一排10个位置中的3个,因疫情防控的需要(这一排没有其他人就座),则每人左右两边都有空位的坐法( )
A.120种 B.80种 C.64种 D.20种
练习:甲、乙、丙、丁、戊5人排成一行,则甲、乙相邻,丙、丁不相邻的排法有( )种
A.24 B.36 C.42 D.48
排队问题
例4:有3名女生、4名男生,在下列不同条件下,求不同的排列方法总数.
(1) 全体排成一排,其中甲必须排在乙左边(甲乙不一定要相邻),有多少种不同的排法?
(2) 全体排成一排,其中甲、乙、丙三人按照其身高从高到低按从左到右进行排列,但可以不相邻,有多少种不同的排法?
(1) 全体排成一排,其中甲必须排在乙左边(甲乙不一定要相邻),有多少种不同的排法?
逐一插空法
(1) 全体排成一排,其中甲必须排在乙左边(甲乙不一定要相邻),有多少种不同的排法?
留空法
如果两个元素的相对位置不变(可以不相邻),可以优先安排好这几个元素,然后将剩下的元素逐一插空,直至所有的元素安排完毕。“逐一插空法”虽然不是最简单的方法,但却是比较好理解好接受的方法。“留空法”在解决定序问题时也是一种比较简便的方法
定序问题(相对位置不变)——逐一插空法或留空法
(2) 全体排成一排,其中甲、乙、丙三人按照其身高从高到低按从左到右进行排列,但可以不相邻,有多少种不同的排法?
(2) 全体排成一排,其中甲、乙、丙三人按照其身高从高到低按从左到右进行排列,但可以不相邻,有多少种不同的排法?
_____,________,________,_______,________,_______,_______
练习:在一张节目表上原有6个节目,如果保持这些节目的相对顺序不变,再添加进去三个节目,求共有多少种安排方法______.
练习(多选题):甲,乙,丙,丁,戊五人并排站成一排,下列说法正确的是( )
A.最左端只能排甲或乙,则不同的排法共有42种
B.如果甲,乙必须相邻且乙在甲的右边,那么不同的排法有24种
C.甲乙丙按从左到右的顺序排列的排法有20种
D.甲乙不相邻的排法种数为36种
练习:有2名老师,3名男生,3名女生站成一排照相留念,在下列情况中,各有多少种不同站法 (结果用具体数字回答)
(1)2名老师不相邻;
(2)3名男生必须站在一起且男生中的甲乙不相邻;
作业:课本P26 习题6.2 5
求解问题问题的6种主要方法
把符合条件的排列数直接列式计算
优先安排特殊元素或特殊位置
把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
对于定序问题,可以优先安排好这几个元素,然后将剩下的元素逐一插空,直至所有的元素安排完毕
正难则反、等价转化的方法
本小节结束
排列组合的综合应用
(排队问题)
分类加法计数原理和分步乘法计数原理
例1.有7名学生,在下列不同条件下,求不同的排列方法总数.
(1)其中男甲排在正中间;
(2)其中男甲不在排头,也不在排尾;
排队问题
有特殊元素或特殊位置的排列组合问题,通常是先排特殊元素或特殊位置,称为优先法;
特殊元素——优先法
排队问题
例2: 有7名学生,在下列不同条件下,求不同的排列方法总数.
(1)7人排成一排,多少种不同的排法?
(2)7人成两排,第一排3人,第二排4人,多少种不同的排法?
(3)7人成三排,第一排1人,第二排2人,第三排4人,多少种不同的排法?
(4)7人成四排,第一排1人,第二排2人,第三排3人,第四排1人,多少种不同的排法?
将元素进行多行排列与元素进行单行排列的本质是一样的,可以用单行排列的方法数来求解,称为多排问题单排法;
多排问题——单排法
排队问题
例3:有3名女生、4名男生,在下列不同条件下,求不同的排列方法总数.
(1)若三个女生要站在一起,有多少种不同的排法?
(2)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
(3)若三个女生互不相邻,有多少种不同的排法?
(4)男生、女生相间排列,有多少种不同的排法?
(1)若三个女生要站在一起,有多少种不同的排法?
元素相邻问题利用“捆绑法”处理,即把相邻元素看作一个整体,视为一个元素,参与其他元素的排列.同时,应注意捆绑元素的内部排列(也就是要记得给他们“松绑”).
相邻问题——捆绑法
(2)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
练习:3名男生和2名女生排成一队照相,要求女生相邻,共有__________种排法.
(3)若三个女生互不相邻,有多少种不同的排法?
插空法
元素不相邻问题利用“插空法”处理,即先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空档中.有多少个空档要根据具体的题目要求来分析。
不相邻问题——插空法
(4)男生、女生相间排列,有多少种不同的排法?
练习:甲 乙 丙三人相约去看电影,他们的座位恰好是同一排10个位置中的3个,因疫情防控的需要(这一排没有其他人就座),则每人左右两边都有空位的坐法( )
A.120种 B.80种 C.64种 D.20种
练习:甲、乙、丙、丁、戊5人排成一行,则甲、乙相邻,丙、丁不相邻的排法有( )种
A.24 B.36 C.42 D.48
排队问题
例4:有3名女生、4名男生,在下列不同条件下,求不同的排列方法总数.
(1) 全体排成一排,其中甲必须排在乙左边(甲乙不一定要相邻),有多少种不同的排法?
(2) 全体排成一排,其中甲、乙、丙三人按照其身高从高到低按从左到右进行排列,但可以不相邻,有多少种不同的排法?
(1) 全体排成一排,其中甲必须排在乙左边(甲乙不一定要相邻),有多少种不同的排法?
逐一插空法
(1) 全体排成一排,其中甲必须排在乙左边(甲乙不一定要相邻),有多少种不同的排法?
留空法
如果两个元素的相对位置不变(可以不相邻),可以优先安排好这几个元素,然后将剩下的元素逐一插空,直至所有的元素安排完毕。“逐一插空法”虽然不是最简单的方法,但却是比较好理解好接受的方法。“留空法”在解决定序问题时也是一种比较简便的方法
定序问题(相对位置不变)——逐一插空法或留空法
(2) 全体排成一排,其中甲、乙、丙三人按照其身高从高到低按从左到右进行排列,但可以不相邻,有多少种不同的排法?
(2) 全体排成一排,其中甲、乙、丙三人按照其身高从高到低按从左到右进行排列,但可以不相邻,有多少种不同的排法?
_____,________,________,_______,________,_______,_______
练习:在一张节目表上原有6个节目,如果保持这些节目的相对顺序不变,再添加进去三个节目,求共有多少种安排方法______.
练习(多选题):甲,乙,丙,丁,戊五人并排站成一排,下列说法正确的是( )
A.最左端只能排甲或乙,则不同的排法共有42种
B.如果甲,乙必须相邻且乙在甲的右边,那么不同的排法有24种
C.甲乙丙按从左到右的顺序排列的排法有20种
D.甲乙不相邻的排法种数为36种
练习:有2名老师,3名男生,3名女生站成一排照相留念,在下列情况中,各有多少种不同站法 (结果用具体数字回答)
(1)2名老师不相邻;
(2)3名男生必须站在一起且男生中的甲乙不相邻;
作业:课本P26 习题6.2 5
求解问题问题的6种主要方法
把符合条件的排列数直接列式计算
优先安排特殊元素或特殊位置
把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
对于定序问题,可以优先安排好这几个元素,然后将剩下的元素逐一插空,直至所有的元素安排完毕
正难则反、等价转化的方法
本小节结束
