北师大版八年级数学下册 1.4 三角形的内角平分线 第2课时 课件(共15张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 1.4 三角形的内角平分线 第2课时 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 00:00:00 | ||
图片预览

文档简介
(共15张PPT)
1.4 角平分线
第一章 三角形的证明
课程讲授
新知导入
随堂练习
课堂小结
第2课时 三角形的内角平分线
知识要点
1.三角形的三条内角平分线相交于一点
2.角平分线的性质和判定的实际应用
锐角三角形
直角三角形
钝角三角形
新知导入
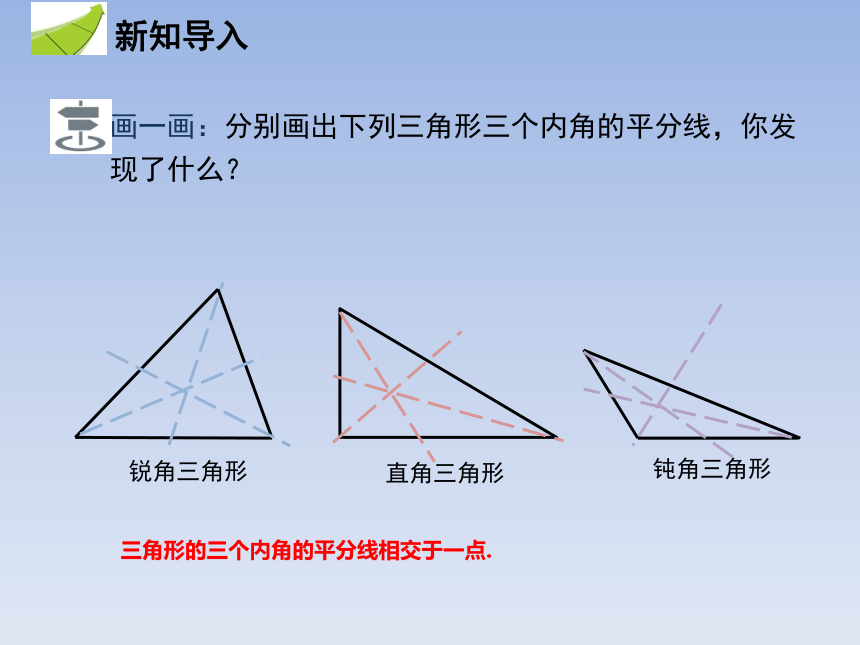
画一画:分别画出下列三角形三个内角的平分线,你发现了什么?
三角形的三个内角的平分线相交于一点.
课程讲授
1
三角形的三条内角平分线相交于一点
锐角三角形
直角三角形
钝角三角形
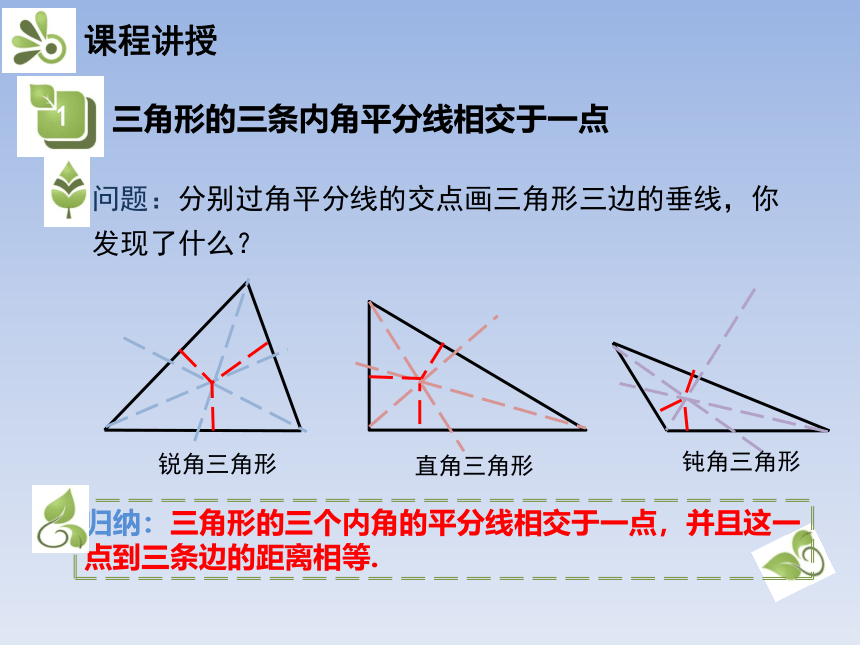
问题:分别过角平分线的交点画三角形三边的垂线,你发现了什么?
归纳:三角形的三个内角的平分线相交于一点,并且这一点到三条边的距离相等.
课程讲授
1
三角形的三条内角平分线相交于一点
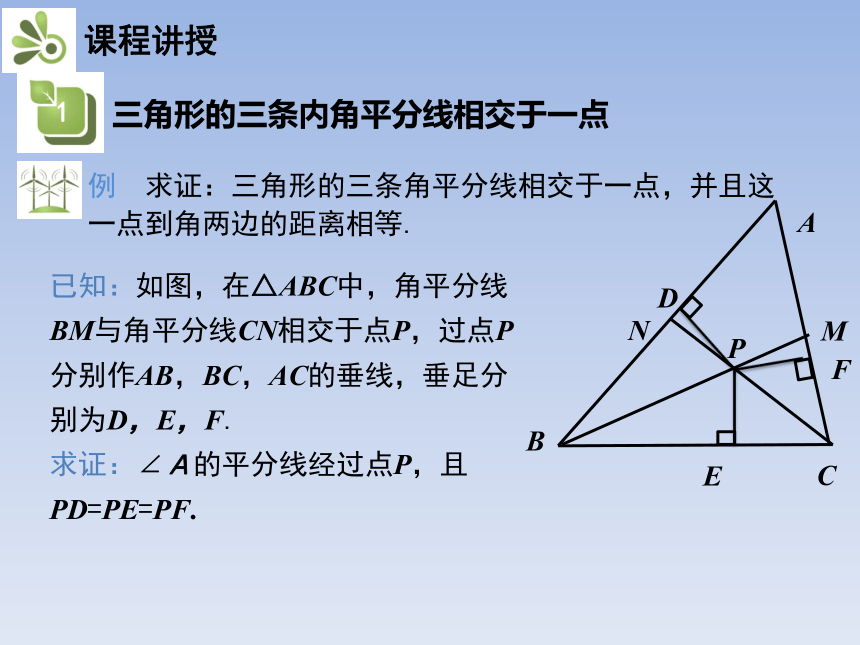
已知:如图,在△ABC中,角平分线BM与角平分线CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别为D,E,F.
求证:∠A的平分线经过点P,且PD=PE=PF.
A
B
C
P
N
M
D
E
F
例 求证:三角形的三条角平分线相交于一点,并且这一点到角两边的距离相等.
课程讲授
1
三角形的三条内角平分线相交于一点
A
B
C
P
N
M
D
E
F
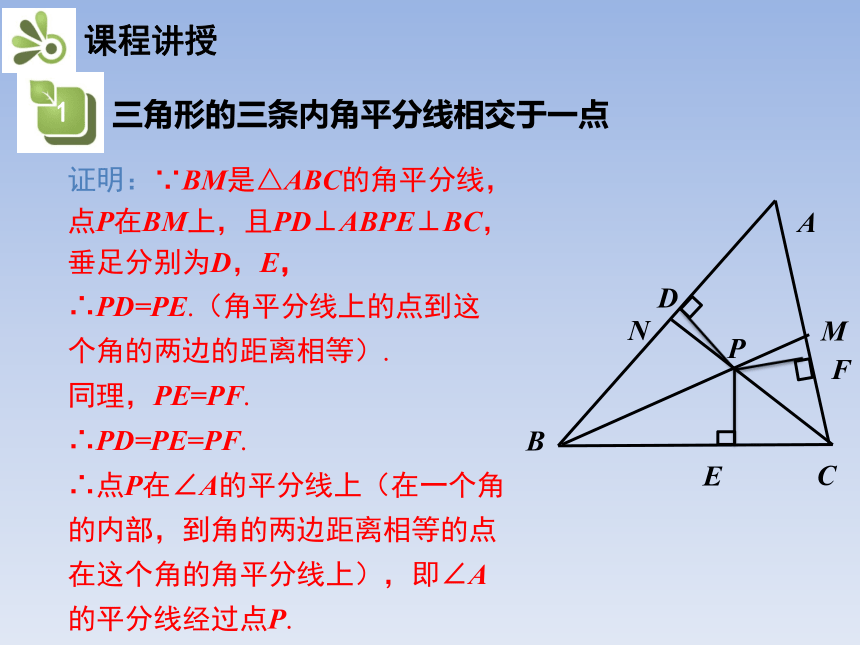
证明:∵BM是△ABC的角平分线,
点P在BM上,且PD⊥ABPE⊥BC,
垂足分别为D,E,
∴PD=PE.(角平分线上的点到这
个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角
的内部,到角的两边距离相等的点
在这个角的角平分线上),即∠A
的平分线经过点P.
课程讲授
1
三角形的三条内角平分线相交于一点
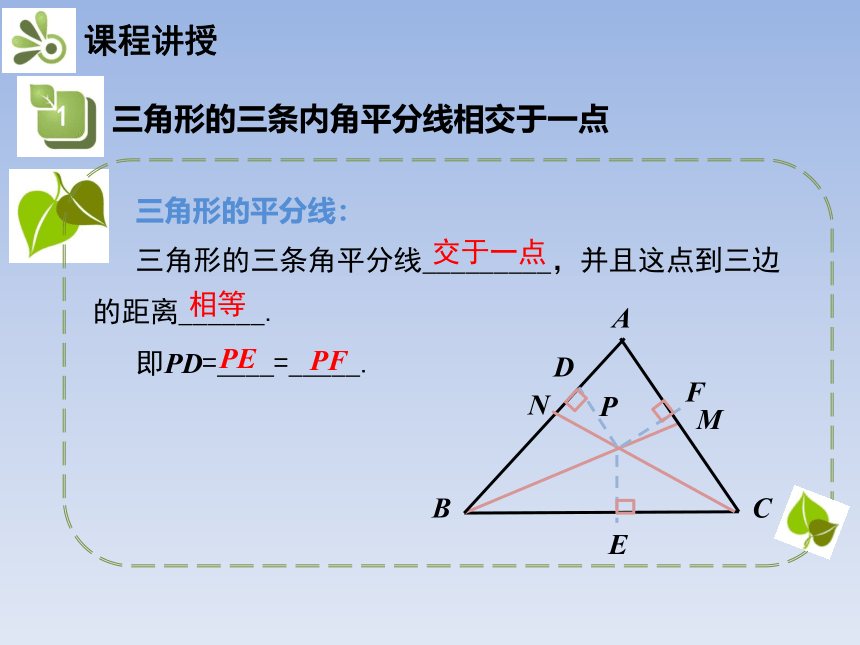
三角形的平分线:
三角形的三条角平分线_________,并且这点到三边的距离______.
即PD=____=_____.
交于一点
相等
A
B
C
P
N
M
D
E
F
PE
PF
课程讲授
1
三角形的三条内角平分线相交于一点
练一练:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,下面结论中正确的是( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.不能确定
B
课程讲授
2
角平分线的性质和判定的实际应用
例 如图,在△ABC中,AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4cm,AC的长;
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线,
DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°. ∴BE=DE.
在等腰直角三角形BDE中,
课程讲授
2
角平分线的性质和判定的实际应用
例 如图,在△ABC中,AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(2)求证:AB=AC+CD.
E
D
A
B
C
(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE(全等三角形的对应边相等).
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
课程讲授
2
角平分线的性质和判定的实际应用
练一练:如图,铁路OA和铁路OB交于O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.
M
(∠AOB的角平分线与AB的交点)
随堂练习
1.如图,△ABC的三边AB,BC,AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC=( )
A.1∶1∶1
B.6∶4∶3
C.2∶3∶4
D.4∶3∶2
C
随堂练习
2.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
A
随堂练习
3.如图,某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭中心的位置.
A
B
C
D
课堂小结
三角形的内角平分线
性质
三角形的三条内角平分线相交于一点,并且这一点到三条边的距离相等
应用
判断一个点是否在角的平分线上;
解决实际问题
1.4 角平分线
第一章 三角形的证明
课程讲授
新知导入
随堂练习
课堂小结
第2课时 三角形的内角平分线
知识要点
1.三角形的三条内角平分线相交于一点
2.角平分线的性质和判定的实际应用
锐角三角形
直角三角形
钝角三角形
新知导入
画一画:分别画出下列三角形三个内角的平分线,你发现了什么?
三角形的三个内角的平分线相交于一点.
课程讲授
1
三角形的三条内角平分线相交于一点
锐角三角形
直角三角形
钝角三角形
问题:分别过角平分线的交点画三角形三边的垂线,你发现了什么?
归纳:三角形的三个内角的平分线相交于一点,并且这一点到三条边的距离相等.
课程讲授
1
三角形的三条内角平分线相交于一点
已知:如图,在△ABC中,角平分线BM与角平分线CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别为D,E,F.
求证:∠A的平分线经过点P,且PD=PE=PF.
A
B
C
P
N
M
D
E
F
例 求证:三角形的三条角平分线相交于一点,并且这一点到角两边的距离相等.
课程讲授
1
三角形的三条内角平分线相交于一点
A
B
C
P
N
M
D
E
F
证明:∵BM是△ABC的角平分线,
点P在BM上,且PD⊥ABPE⊥BC,
垂足分别为D,E,
∴PD=PE.(角平分线上的点到这
个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P在∠A的平分线上(在一个角
的内部,到角的两边距离相等的点
在这个角的角平分线上),即∠A
的平分线经过点P.
课程讲授
1
三角形的三条内角平分线相交于一点
三角形的平分线:
三角形的三条角平分线_________,并且这点到三边的距离______.
即PD=____=_____.
交于一点
相等
A
B
C
P
N
M
D
E
F
PE
PF
课程讲授
1
三角形的三条内角平分线相交于一点
练一练:如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,下面结论中正确的是( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.不能确定
B
课程讲授
2
角平分线的性质和判定的实际应用
例 如图,在△ABC中,AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)已知CD=4cm,AC的长;
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线,
DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°. ∴BE=DE.
在等腰直角三角形BDE中,
课程讲授
2
角平分线的性质和判定的实际应用
例 如图,在△ABC中,AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(2)求证:AB=AC+CD.
E
D
A
B
C
(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE(全等三角形的对应边相等).
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
课程讲授
2
角平分线的性质和判定的实际应用
练一练:如图,铁路OA和铁路OB交于O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.
M
(∠AOB的角平分线与AB的交点)
随堂练习
1.如图,△ABC的三边AB,BC,AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC=( )
A.1∶1∶1
B.6∶4∶3
C.2∶3∶4
D.4∶3∶2
C
随堂练习
2.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110° B.120° C.130° D.140°
A
随堂练习
3.如图,某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭中心的位置.
A
B
C
D
课堂小结
三角形的内角平分线
性质
三角形的三条内角平分线相交于一点,并且这一点到三条边的距离相等
应用
判断一个点是否在角的平分线上;
解决实际问题
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
