北师大版八年级下册2 不等式的基本性质课件(共17张PPT)
文档属性
| 名称 | 北师大版八年级下册2 不等式的基本性质课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 09:58:23 | ||
图片预览





文档简介
(共17张PPT)
2.2 不等式的基本性质
第二章 一元一次不等式与
一元一次不等式组
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.不等式的基本性质
2.利用不等式的性质把不等式化成“x>a”或“x新知导入
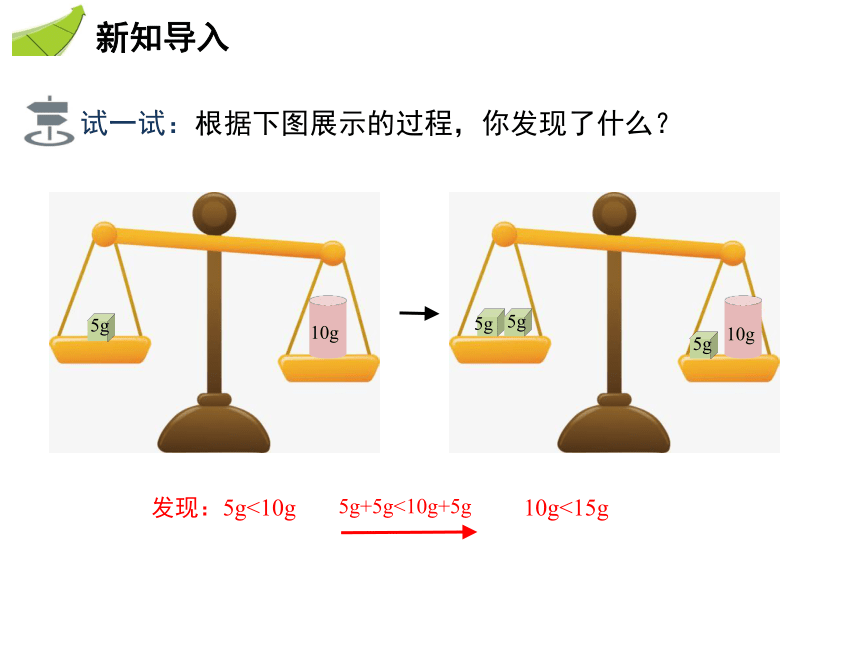
试一试:根据下图展示的过程,你发现了什么?
5g
10g
5g
5g
5g
10g
发现:5g<10g
10g<15g
5g+5g<10g+5g
课程讲授
1
不等式的基本性质
问题1:用“﹥”或“﹤”填空,并总结其中的规律:
(1)5>3,5+2 3+2, 5-2 3-2 ;
(2)-1<3,-1+2 3+2, -1-3 3-3 .
>
>
<
<
规律:若a>b,则a+c > b+c,a-c > b-c;
若a课程讲授
1
不等式的基本性质
不等式的基本性质1:
不等式的两边都加 (或减) 同一个整式,不等号的方向不变.
课程讲授
1
不等式的基本性质
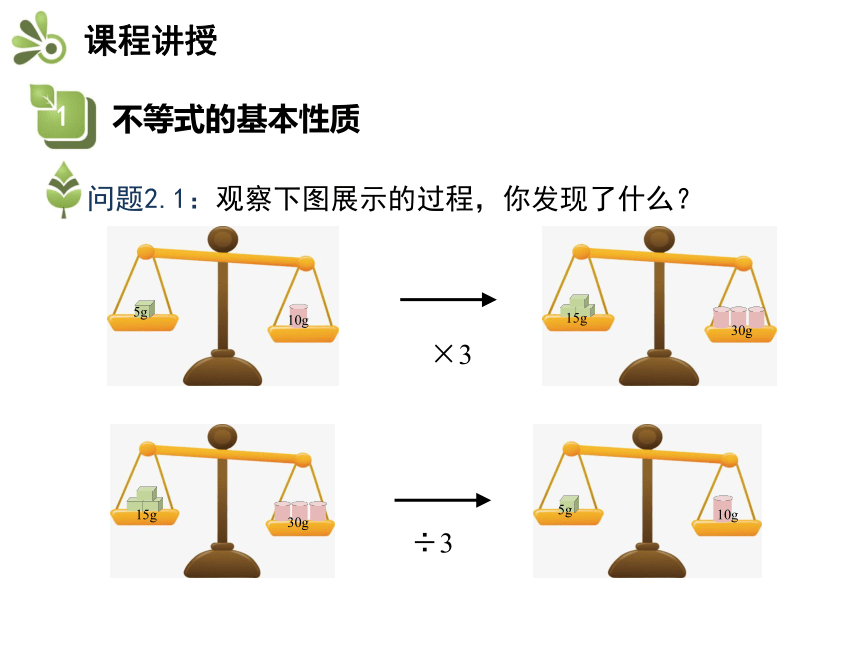
问题2.1:观察下图展示的过程,你发现了什么?
×3
÷3
5g
10g
15g
30g
15g
30g
5g
10g
课程讲授
1
不等式的基本性质
问题2.2:用“<”或“>”填空,并总结其中的规律:
>
>
<
<
(1)6>2,
6×5___2×5,6×(-5)___2 ×(-5);
(2)-2<3,
(-2)×6___3×6,(-2)×(-6)___3 ×(-6).
课程讲授
1
不等式的基本性质
不等式的基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向 .
不等式的基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向 .
不变
改变
课程讲授
1
不等式的基本性质
练一练:选择适当的不等号填空,并说明理由.
>
>
>
课程讲授
1
不等式的基本性质
想一想:上节课,我们猜想,无论绳长 l 取何值,圆的面积总大于正方形的面积,即 .你相信这个结论吗?你能用不等式的性质证明吗?
证明:不等式的两边都乘以16,由不等式的基本性质2,得
不等式的两边都除以 l2,由不等式的基本性质2,得
因为上式是恒等式,所以 也为恒等式.
课程讲授
2
利用不等式的性质把不等式化成“x>a”或“x例 将下列不等式化成“x>a”或“x<a”的形式:
(1)x-5>-1;(2)-2x>3.
解:(1)根据不等式的基本性质1,两边都加5,得x> -1 +5,即x > 4.
(2)根据不等式的基本性质3,两边都除以-2,得
课程讲授
2
利用不等式的性质把不等式化成“x>a”或“x想一想:把不等式逐步转化为“x>a”或“x将不等式逐步转化为“x>a”或“x课程讲授
2
利用不等式的性质把不等式化成“x>a”或“x练一练: 把下列不等式化为x>a或x(1)5>3+x;(2)x-9>3;(3)2x<x+6.
解:(1)x < 2.
(2)x>12.
(3)x < 6.
随堂练习
1.已知a<0,试比较2a与a的大小.
解:利用不等式的基本性质2:
∵a<0,
∴ a+a<0+a,
即2a <a.
随堂练习
2.把下列不等式化为x>a或x(1) ; (2) ;
(3) ; (4) .
解:(1)
(2)
(3)
(4)
随堂练习
3.若x > y,比较2-3x与2-3y的大小,并说明理由.
解:∵x>y,
∴-3x<-3y,(不等式的基本性质3)
∴2-3x<2-3y.(不等式的基本性质1)
课堂小结
不等式的基本性质
不等式的基本性质
利用不等式的性质把不等式化成“x>a”或“x不等式的基本性质1:不等式的两边都加 (或减) 同一个整式,不等号的方向不变
不等式的基本性质2: 不等式的两边都乘(或除以)同一个正数,不等号的方向不变
不等式基本性质3:不等式的两边都乘(或除以)同一个负数,不等号的方向改变
2.2 不等式的基本性质
第二章 一元一次不等式与
一元一次不等式组
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.不等式的基本性质
2.利用不等式的性质把不等式化成“x>a”或“x
试一试:根据下图展示的过程,你发现了什么?
5g
10g
5g
5g
5g
10g
发现:5g<10g
10g<15g
5g+5g<10g+5g
课程讲授
1
不等式的基本性质
问题1:用“﹥”或“﹤”填空,并总结其中的规律:
(1)5>3,5+2 3+2, 5-2 3-2 ;
(2)-1<3,-1+2 3+2, -1-3 3-3 .
>
>
<
<
规律:若a>b,则a+c > b+c,a-c > b-c;
若a
1
不等式的基本性质
不等式的基本性质1:
不等式的两边都加 (或减) 同一个整式,不等号的方向不变.
课程讲授
1
不等式的基本性质
问题2.1:观察下图展示的过程,你发现了什么?
×3
÷3
5g
10g
15g
30g
15g
30g
5g
10g
课程讲授
1
不等式的基本性质
问题2.2:用“<”或“>”填空,并总结其中的规律:
>
>
<
<
(1)6>2,
6×5___2×5,6×(-5)___2 ×(-5);
(2)-2<3,
(-2)×6___3×6,(-2)×(-6)___3 ×(-6).
课程讲授
1
不等式的基本性质
不等式的基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向 .
不等式的基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向 .
不变
改变
课程讲授
1
不等式的基本性质
练一练:选择适当的不等号填空,并说明理由.
>
>
>
课程讲授
1
不等式的基本性质
想一想:上节课,我们猜想,无论绳长 l 取何值,圆的面积总大于正方形的面积,即 .你相信这个结论吗?你能用不等式的性质证明吗?
证明:不等式的两边都乘以16,由不等式的基本性质2,得
不等式的两边都除以 l2,由不等式的基本性质2,得
因为上式是恒等式,所以 也为恒等式.
课程讲授
2
利用不等式的性质把不等式化成“x>a”或“x
(1)x-5>-1;(2)-2x>3.
解:(1)根据不等式的基本性质1,两边都加5,得x> -1 +5,即x > 4.
(2)根据不等式的基本性质3,两边都除以-2,得
课程讲授
2
利用不等式的性质把不等式化成“x>a”或“x
2
利用不等式的性质把不等式化成“x>a”或“x
解:(1)x < 2.
(2)x>12.
(3)x < 6.
随堂练习
1.已知a<0,试比较2a与a的大小.
解:利用不等式的基本性质2:
∵a<0,
∴ a+a<0+a,
即2a <a.
随堂练习
2.把下列不等式化为x>a或x
(3) ; (4) .
解:(1)
(2)
(3)
(4)
随堂练习
3.若x > y,比较2-3x与2-3y的大小,并说明理由.
解:∵x>y,
∴-3x<-3y,(不等式的基本性质3)
∴2-3x<2-3y.(不等式的基本性质1)
课堂小结
不等式的基本性质
不等式的基本性质
利用不等式的性质把不等式化成“x>a”或“x
不等式的基本性质2: 不等式的两边都乘(或除以)同一个正数,不等号的方向不变
不等式基本性质3:不等式的两边都乘(或除以)同一个负数,不等号的方向改变
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
