15.1全等三角形
图片预览





文档简介
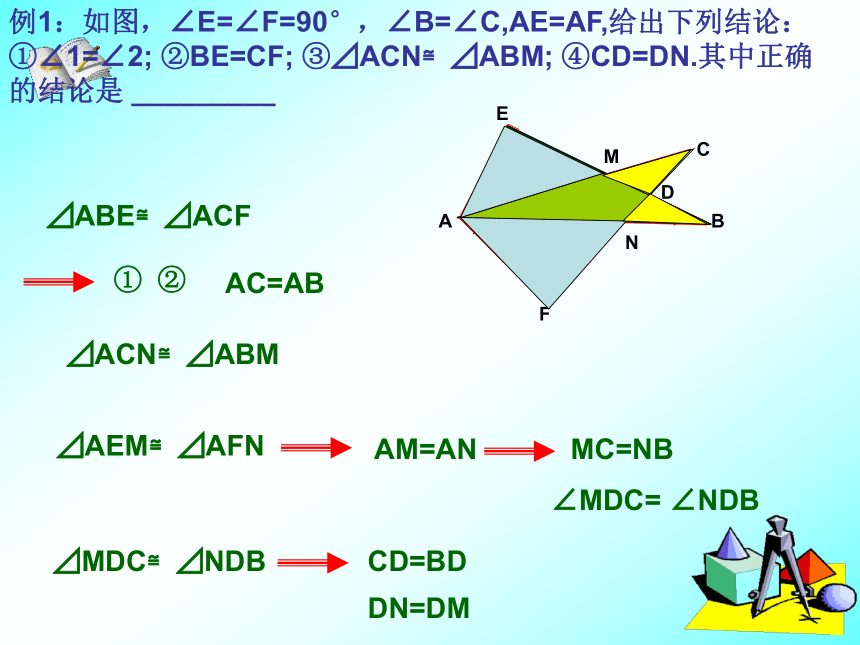
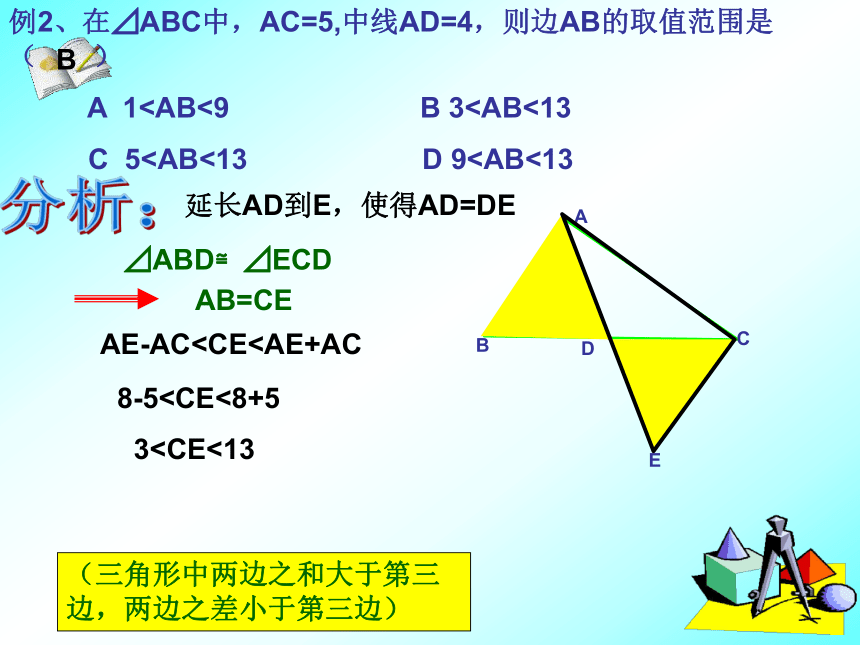
课件35张PPT。全等三角形例1:如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2; ②BE=CF; ③⊿ACN≌⊿ABM; ④CD=DN.其中正确的结论是 _________CBFEAD12MN⊿ABE≌⊿ACF①②AC=AB⊿ACN≌⊿ABM⊿AEM≌⊿AFNAM=ANMC=NB∠MDC= ∠NDB⊿MDC≌⊿NDBCD=BDDN=DM例2、在⊿ABC中,AC=5,中线AD=4,则边AB的取值范围是( )
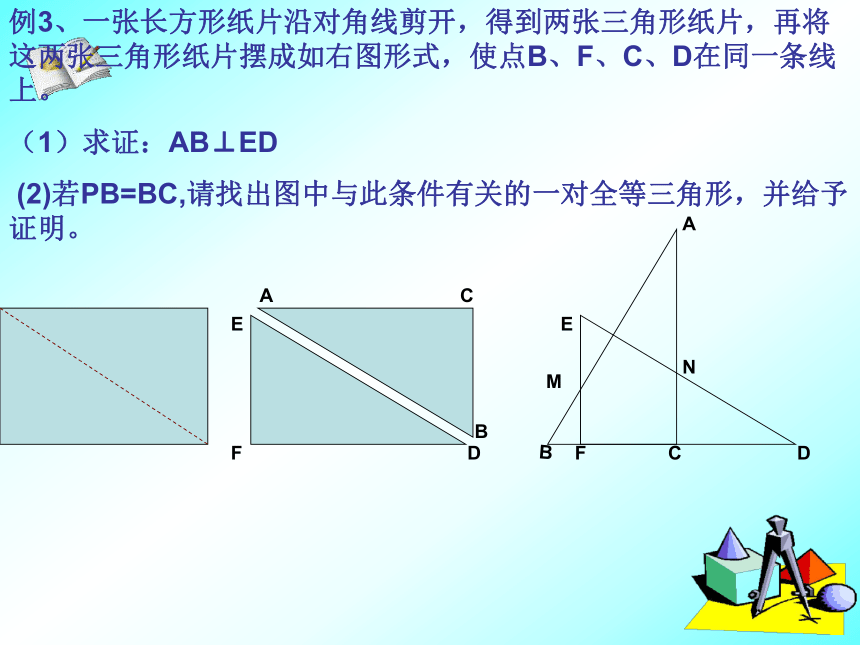
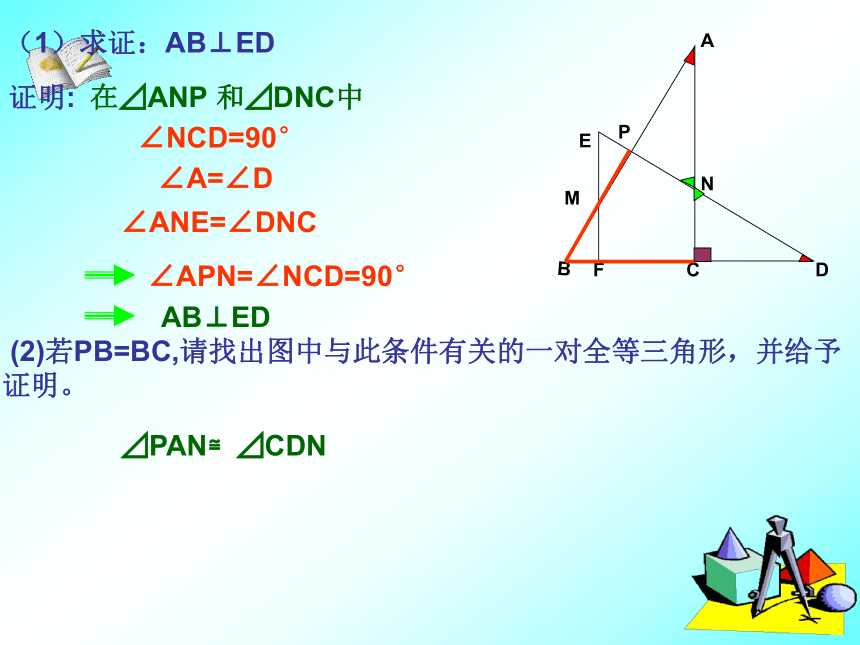
A 1 C 5(1)求证:AB⊥ED
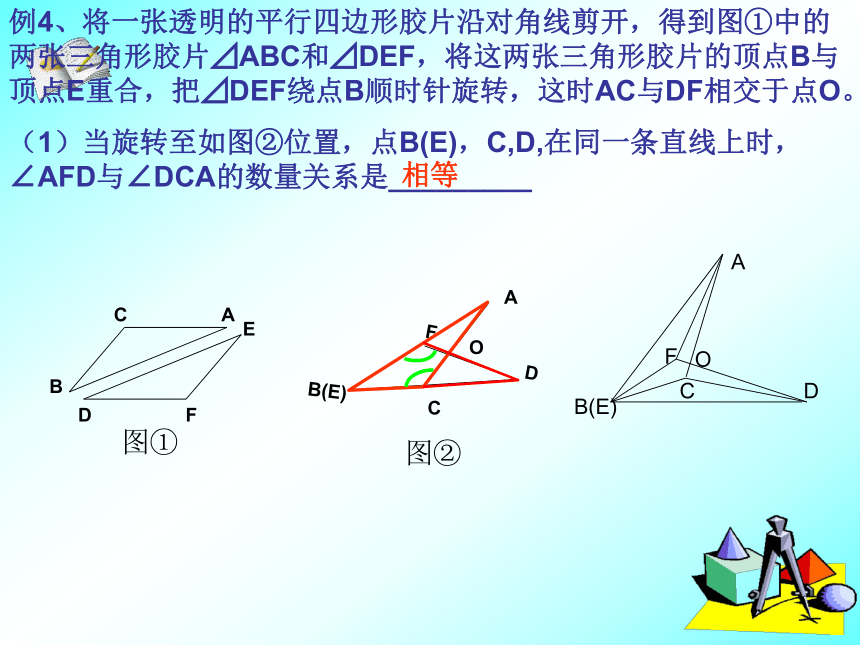
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明。(1)求证:AB⊥ED (2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明。∠A=∠D∠NCD=90°∠ANE=∠DNC在⊿ANP 和⊿DNC中P证明:∠APN=∠NCD=90°AB⊥ED⊿PAN≌⊿CDN例4、将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片⊿ABC和⊿DEF,将这两张三角形胶片的顶点B与顶点E重合,把⊿DEF绕点B顺时针旋转,这时AC与DF相交于点O。
(1)当旋转至如图②位置,点B(E),C,D,在同一条直线上时,∠AFD与∠DCA的数量关系是_________
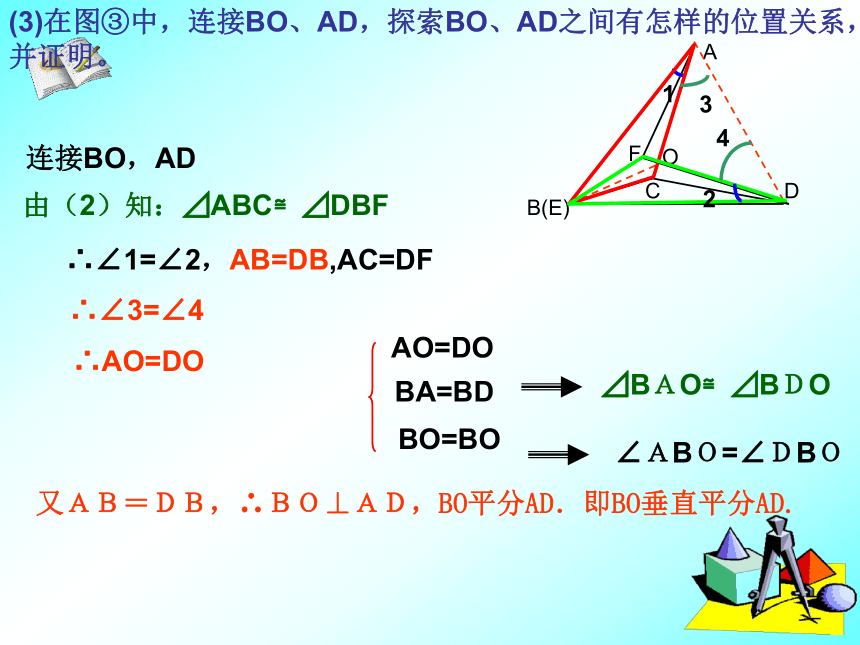
图①图②相等(2)当⊿DEF旋转至如图③位置时,(1)中的结论还成立吗?请说明理由;图①图②图③⊿ABC≌⊿DBF⊿ABF≌⊿DBCBC=BFBA=BD∠ABC=∠DBF∠ABF=∠DBC∠BAF=∠BDC∠AFD=∠DCA(3)在图③中,连接BO、AD,探索BO、AD之间有怎样的位置关系,并证明。连接BO,AD由(2)知:⊿ABC≌⊿DBF12∴∠1=∠2,AB=DB,AC=DF∴∠3=∠4∴AO=DO又AB=DB,∴BO⊥AD,BO平分AD.即BO垂直平分AD.⊿BAO≌⊿BDO∠ABO=∠DBO例5 如图 点C在线段AB上,DA⊥AB, EB⊥AB ,FC⊥AB,且DA=BC,EB=AC,FC=AB, ∠AFB=51°,求∠DFE的度数。∠DFE= ∠AFB- ∠AFD- ∠EFB分析: Rt⊿DAB≌Rt⊿BCFBD=BF∠DBA=∠BFC∠BDA=∠FBC∠DBF= ∠DBA+∠FBC= 90°∠BDF=∠BFD=45°∠DFA=51°-45°=6°同理:∠DFB=6°∠DFE=51°-6°-6°=39°证明:在Rt⊿DAB和Rt⊿BCF中基础夯实1、如图,⊿AOB中,∠B=30°,将⊿AOB绕点O顺时针旋转52°得到∠ ,则∠ 的度数为________52°三角形的一个外角等于不相邻的两个内角的和。82°2、如图,OA=OB,OC=OD,∠O=60°, ∠C=25°,则∠BED等于_____________60°∠CBD=60°+25°=85°OA=OBOC=OD∠O=∠O⊿AOD≌⊿BOC∠C=∠D=25°∠BED=180°-85°-25°=70°70°3、如图,把大小为4×4的正方形方格图形分割成两个全等图形,例如图1,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分成两个全等图形。画法1画法4画法3图1画法2两部分有何关系?关于正方形中心对称4、如图,⊿ABE和⊿ADC是⊿ABC分别沿着AB、AC边翻折180°形成的,若∠1: ∠2 :∠3=28:5:3,则 的度数为
__________∠1=140° ∠2=25°∠3=15°80°5、如图,在⊿ABC中,AD⊥BC于D,CE⊥AB于E,AD、CE交于点H,已知EH=EB=3,AE=4.则CH的长是( )A、 1 B 、 2 C、3 D、4 AE=CE=4⊿AEH≌⊿CEBCE-EH=4-3=1A6、如图,A在DE上,F在AB上,且AC=CE, ∠1=∠2=∠3,则DE的长等于( )
A、DC B、BC C、AB D 、AE+AC∠D=180°-∠DFA-∠1∠B=180°-∠BFA-∠2∠1=∠2=∠3∠D= ∠B AC=CE∠1=∠2=∠3∠BCA=∠DCE∠DCE=∠BCA⊿ABC≌⊿EDCDE=ABC点评:要寻找与已知条件相关的一对全等三角形。7、如图,AB∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对
A 5 B 6 C 7 D 8C8、两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线
(1)图中有多少对全等三角形?并将它们写出来;
(2)选择其中一对(⊿ABC≌⊿A1B1C1除外)进行证明。(1)3对AC1=A1C∠A=∠A1(2)⊿AEC1≌⊿A1FC9、两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);图1图2(2)证明:DC⊥BE图1又∠ACB=45°∠ABE=∠ACD=45°∴ ∠ACB+∠ACD=45°+45°=90°由(1)⊿ABE≌⊿ACD图210、在⊿ABC中,∠ACB=90°AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE证明:∠1+∠3=90°∵∠1+∠2=90°,∴ ∠2=∠3又∵∠ADC= ∠CEB=90°,AC=BC∴ ⊿ADC≌⊿CEB∴ AD=CE,CD=BE∴ DE=CD+CE=AD+BE即,DE=AD+BE10、在⊿ABC中,∠ACB=90°AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE证明:∠BCE+∠CBE=90°∵∠ACD+∠BCE=90°,∴ ∠ACD=∠CBE∴ ⊿ADC≌⊿CEB∴ AD=CE,CD=BE∴ DE=CE-CD=AD-BE即,DE=AD-BE又∵∠ADC= ∠CEB=90°,AC=BC10、在⊿ABC中,∠ACB=90°AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系?请写出这个等量关系,并加以证明。DE=BE-AD提示:能力拓展:11、在⊿ABC中,高AD和BE 交于H点,且BH=AC,则∠ABC=_________⊿BDH≌⊿ADCAD=BD∠ABC=BAD=45°135°45°或135°12、如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC, ∠BAE=36°,那么∠BED=__________∠BED= ∠BFC= ∠ABF +∠BAF= ∠ABF +2∠BAE =90°-36° +2×36°=126°126°ED∥AC,(同位角相等)13、如图,D是⊿ABC的边上一点,DF交AC于点E,给出三个论断:①DE=FE;②AE=CE; ③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出三个命题,其中正确的个数是_______√√√314、如图,在⊿ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是__________⊿ADC≌⊿EDBAC=EB=3AB-EBA 、1 B 、2 C、 3 D、 4⊿ACD≌⊿BCF①AD=BF; ② CF=CD; AC+CD=AC+CF=AF?ABE≌?AFE∴AB=AF,③成立.⑤BF=2BED16、如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是( )
A、AB-AD>CB-CD B、AB-AD=CB-CD
C、 AB-ADCB-CDBE=AB-AE=AB-AD>CB-CDA17、考查下列命题:①全等三角形的对应边上的中线、高、角平分线对应相等;②两边和其中一边上的中线(或第三边上的中线)对应相等的两个三角形全等;③两角和其中一角的角平分线(或第三角的角平分线)对应相等的两个三角形全等;④两边和其中一边上的高(或第三边上的高)对应相等的两个三角形全等。
其中正确的个数有( )
A、 4个 B、3个 C、2 个 D、 1个B×18、若两个三角形的两边和其中一边上的高分别对应相等,则这两个三角形第三边所对的角的关系是( )
A、相等 B、互余 C、互补 D、 相等或互补D相等互补19、如图,⊿ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF的大小关系,并证明你的结论。∴⊿BDE≌⊿CDP延长ED至P,使DP=DE,并连接FP,CP∴⊿EDF≌⊿PDFEF=PFBE=CP在⊿PFC中,PF∠AOE=∠DOC=60°=∠FOCF22、如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上的两点,且∠BEC=∠CFA=∠(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°, ,则BE___CF;
EF_____ (填<,>或者=)
②如图2,若0°< ∠BCA<180°,请添加一个关于 与∠BCA关系的条件______,使①中的两个结论仍然成立,并证明这两个结论。
(2)如图3,若直线CD经过∠BCA的外部, = ∠BCA,请提出EF、BE、AF三条线段数量关系的合理猜想(不要求证明)ADFCBE图1ADFCBE图2(1)证?BCE≌?CAF,可得
BE=CF,EF=︱BE-AF︱;(3)证?BEC≌?CFA
可得EF=BE+AF(2)∠a+∠BCA=180°;
A 1
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明。(1)求证:AB⊥ED (2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明。∠A=∠D∠NCD=90°∠ANE=∠DNC在⊿ANP 和⊿DNC中P证明:∠APN=∠NCD=90°AB⊥ED⊿PAN≌⊿CDN例4、将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片⊿ABC和⊿DEF,将这两张三角形胶片的顶点B与顶点E重合,把⊿DEF绕点B顺时针旋转,这时AC与DF相交于点O。
(1)当旋转至如图②位置,点B(E),C,D,在同一条直线上时,∠AFD与∠DCA的数量关系是_________
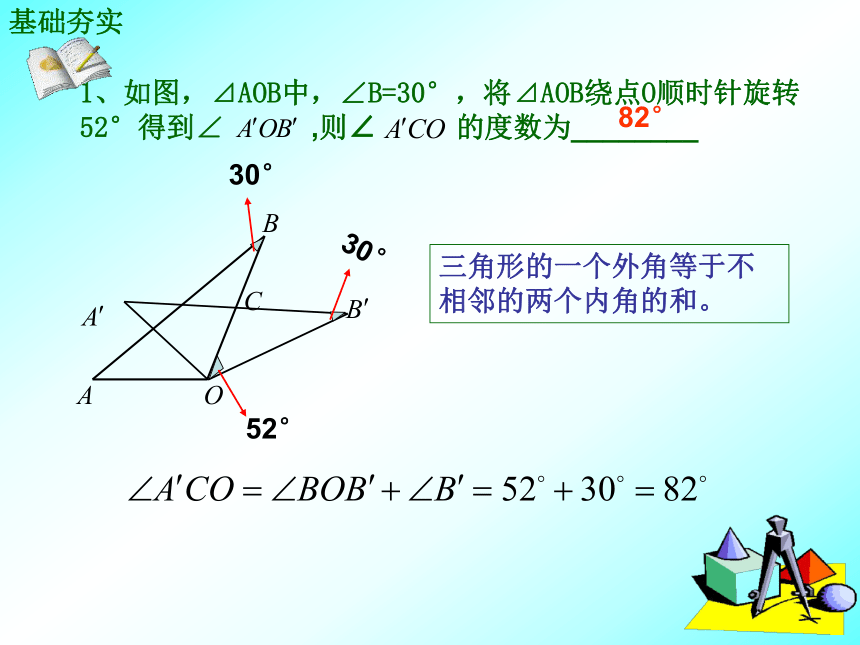
图①图②相等(2)当⊿DEF旋转至如图③位置时,(1)中的结论还成立吗?请说明理由;图①图②图③⊿ABC≌⊿DBF⊿ABF≌⊿DBCBC=BFBA=BD∠ABC=∠DBF∠ABF=∠DBC∠BAF=∠BDC∠AFD=∠DCA(3)在图③中,连接BO、AD,探索BO、AD之间有怎样的位置关系,并证明。连接BO,AD由(2)知:⊿ABC≌⊿DBF12∴∠1=∠2,AB=DB,AC=DF∴∠3=∠4∴AO=DO又AB=DB,∴BO⊥AD,BO平分AD.即BO垂直平分AD.⊿BAO≌⊿BDO∠ABO=∠DBO例5 如图 点C在线段AB上,DA⊥AB, EB⊥AB ,FC⊥AB,且DA=BC,EB=AC,FC=AB, ∠AFB=51°,求∠DFE的度数。∠DFE= ∠AFB- ∠AFD- ∠EFB分析: Rt⊿DAB≌Rt⊿BCFBD=BF∠DBA=∠BFC∠BDA=∠FBC∠DBF= ∠DBA+∠FBC= 90°∠BDF=∠BFD=45°∠DFA=51°-45°=6°同理:∠DFB=6°∠DFE=51°-6°-6°=39°证明:在Rt⊿DAB和Rt⊿BCF中基础夯实1、如图,⊿AOB中,∠B=30°,将⊿AOB绕点O顺时针旋转52°得到∠ ,则∠ 的度数为________52°三角形的一个外角等于不相邻的两个内角的和。82°2、如图,OA=OB,OC=OD,∠O=60°, ∠C=25°,则∠BED等于_____________60°∠CBD=60°+25°=85°OA=OBOC=OD∠O=∠O⊿AOD≌⊿BOC∠C=∠D=25°∠BED=180°-85°-25°=70°70°3、如图,把大小为4×4的正方形方格图形分割成两个全等图形,例如图1,请在下图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分成两个全等图形。画法1画法4画法3图1画法2两部分有何关系?关于正方形中心对称4、如图,⊿ABE和⊿ADC是⊿ABC分别沿着AB、AC边翻折180°形成的,若∠1: ∠2 :∠3=28:5:3,则 的度数为
__________∠1=140° ∠2=25°∠3=15°80°5、如图,在⊿ABC中,AD⊥BC于D,CE⊥AB于E,AD、CE交于点H,已知EH=EB=3,AE=4.则CH的长是( )A、 1 B 、 2 C、3 D、4 AE=CE=4⊿AEH≌⊿CEBCE-EH=4-3=1A6、如图,A在DE上,F在AB上,且AC=CE, ∠1=∠2=∠3,则DE的长等于( )
A、DC B、BC C、AB D 、AE+AC∠D=180°-∠DFA-∠1∠B=180°-∠BFA-∠2∠1=∠2=∠3∠D= ∠B AC=CE∠1=∠2=∠3∠BCA=∠DCE∠DCE=∠BCA⊿ABC≌⊿EDCDE=ABC点评:要寻找与已知条件相关的一对全等三角形。7、如图,AB∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对
A 5 B 6 C 7 D 8C8、两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线
(1)图中有多少对全等三角形?并将它们写出来;
(2)选择其中一对(⊿ABC≌⊿A1B1C1除外)进行证明。(1)3对AC1=A1C∠A=∠A1(2)⊿AEC1≌⊿A1FC9、两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);图1图2(2)证明:DC⊥BE图1又∠ACB=45°∠ABE=∠ACD=45°∴ ∠ACB+∠ACD=45°+45°=90°由(1)⊿ABE≌⊿ACD图210、在⊿ABC中,∠ACB=90°AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE证明:∠1+∠3=90°∵∠1+∠2=90°,∴ ∠2=∠3又∵∠ADC= ∠CEB=90°,AC=BC∴ ⊿ADC≌⊿CEB∴ AD=CE,CD=BE∴ DE=CD+CE=AD+BE即,DE=AD+BE10、在⊿ABC中,∠ACB=90°AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE证明:∠BCE+∠CBE=90°∵∠ACD+∠BCE=90°,∴ ∠ACD=∠CBE∴ ⊿ADC≌⊿CEB∴ AD=CE,CD=BE∴ DE=CE-CD=AD-BE即,DE=AD-BE又∵∠ADC= ∠CEB=90°,AC=BC10、在⊿ABC中,∠ACB=90°AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系?请写出这个等量关系,并加以证明。DE=BE-AD提示:能力拓展:11、在⊿ABC中,高AD和BE 交于H点,且BH=AC,则∠ABC=_________⊿BDH≌⊿ADCAD=BD∠ABC=BAD=45°135°45°或135°12、如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC, ∠BAE=36°,那么∠BED=__________∠BED= ∠BFC= ∠ABF +∠BAF= ∠ABF +2∠BAE =90°-36° +2×36°=126°126°ED∥AC,(同位角相等)13、如图,D是⊿ABC的边上一点,DF交AC于点E,给出三个论断:①DE=FE;②AE=CE; ③FC∥AB,以其中一个论断为结论,其余两个论断为条件,可作出三个命题,其中正确的个数是_______√√√314、如图,在⊿ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是__________⊿ADC≌⊿EDBAC=EB=3AB-EB
A、AB-AD>CB-CD B、AB-AD=CB-CD
C、 AB-AD
其中正确的个数有( )
A、 4个 B、3个 C、2 个 D、 1个B×18、若两个三角形的两边和其中一边上的高分别对应相等,则这两个三角形第三边所对的角的关系是( )
A、相等 B、互余 C、互补 D、 相等或互补D相等互补19、如图,⊿ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF的大小关系,并证明你的结论。∴⊿BDE≌⊿CDP延长ED至P,使DP=DE,并连接FP,CP∴⊿EDF≌⊿PDFEF=PFBE=CP在⊿PFC中,PF
①如图1,若∠BCA=90°, ,则BE___CF;
EF_____ (填<,>或者=)
②如图2,若0°< ∠BCA<180°,请添加一个关于 与∠BCA关系的条件______,使①中的两个结论仍然成立,并证明这两个结论。
(2)如图3,若直线CD经过∠BCA的外部, = ∠BCA,请提出EF、BE、AF三条线段数量关系的合理猜想(不要求证明)ADFCBE图1ADFCBE图2(1)证?BCE≌?CAF,可得
BE=CF,EF=︱BE-AF︱;(3)证?BEC≌?CFA
可得EF=BE+AF(2)∠a+∠BCA=180°;
