数学人教A版(2019)必修第二册10.3.2随机模拟(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册10.3.2随机模拟(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 197.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 18:43:45 | ||
图片预览






文档简介
(共19张PPT)
高一数学第二册第十章:概率
10.3.2 随 机 模 拟
1.理解随机数的产生;
2.了解随机模拟方法确定概率的估计值;
3.会利用随机数来求简单事件的概率.
一、学习目标
二、问题导学
阅读教材255--257,回答下列问题:
思考:用频率估计概率,需要做大量的重复试验.有没有其他方法可以替代试验呢
随机模拟
随机数:例如我们要产生0~9之间的随机整数, 像彩票摇奖那样,把10个质地和大小相同的号码球放入摇奖器中,充分搅拌后摇出一个球,这个球上的号码就称为随机数.
伪随机数:计算器或计算机产生的随机数是按照确定的算法产生的数,具有周期性(周期很长),它们具有类似随机数的性质.因此,计算器或计算机产生的随机数不是真正的随机数,我们称它们为伪随机数
三、点拨精讲(25分钟)
1、随机模拟产生的原因:
用频率估计概率,需要做大量的重复试验,费时、费力,甚至难以实现.
2、随机模拟的方法:
利用计算器或计算软件产生随机数(根据不同的随机试验构建相应的随机数模拟试验)
又如,一个袋中装有2个红球和3个白球,这些球除颜色不同外没有其他差别. 对于从袋中摸出一个球的试验,我们可以让计算器或计算机产生取值于集合{1,2,3,4,5}的随机数,用1、2表示红球,用3、4、5表示白球. 这样不断产生1~5之间的整数随机数,相当于不断地做从袋中摸球的试验.
例如,对于抛掷一枚质地均匀硬币的试验,我们可以让计算器或计算机产生取值于集合{0,1} 的随机数,用0表示反面朝上,用1表示正面朝上.这样不断产生0、1两个随机数,相当于不断地做抛掷硬币的试验.
做整数随机模拟试验时,首先要确定随机数的范围,明确哪个数字代表哪个试验结果.
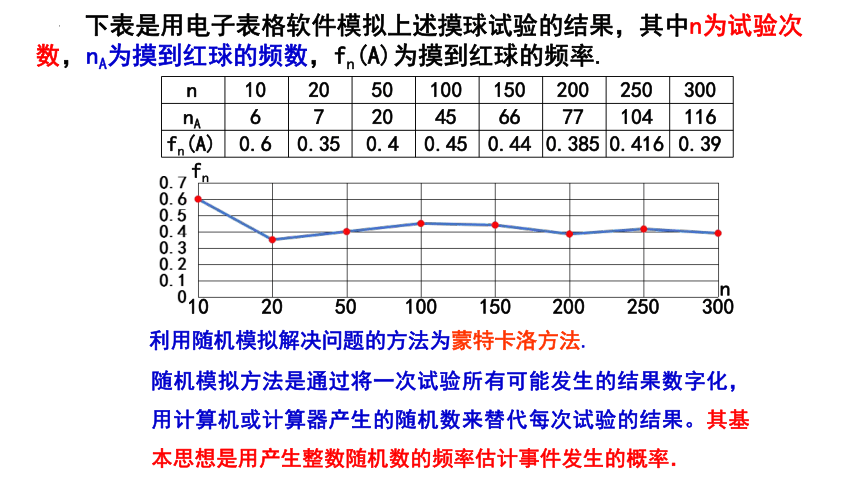
下表是用电子表格软件模拟上述摸球试验的结果,其中n为试验次数,nA为摸到红球的频数,fn(A)为摸到红球的频率.
n 10 20 50 100 150 200 250 300
nA 6 7 20 45 66 77 104 116
fn(A) 0.6 0.35 0.4 0.45 0.44 0.385 0.416 0.39
fn
n
10
20
50
100
150
200
250
300
利用随机模拟解决问题的方法为蒙特卡洛方法.
随机模拟方法是通过将一次试验所有可能发生的结果数字化,用计算机或计算器产生的随机数来替代每次试验的结果。其基本思想是用产生整数随机数的频率估计事件发生的概率.
例1 从你所在班级任意选出6名同学,调查他们的出生月份,假设
出生在一月,二月,…,十二月是等可能的.设事件A =“至少
有两人出生月份相同”,设计一种试验方法,模拟20次,估计
事件A发生的概率.
解:(法一随机数法)根据假设,每个人的出生月份在12个月中是等可能的,而且相互之间没有影响,所以观察6个人的出生月份可以看成可重复试验.
因此,可以构建如下有放回摸球试验进行模拟:在袋子中装入编号为1,2,…,12的12个球,这些球除编号外没有什么差别.有放回地随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验.如果这6个数中至少有2个相同,表示事件A发生了. 重复以上模拟试验20次,就可以统计出事件A发生的频率.
例1 从你所在班级任意选出6名同学,调查他们的出生月份,假设
出生在一月,二月,…,十二月是等可能的.设事件A =“至少
有两人出生月份相同”,设计一种试验方法,模拟20次,估计
事件A发生的概率.
(法二:计算机模拟,伪随机数)利用电子表格软件模拟试验. 在A1、B1、C1、D1、E1、F1单元格分别输人“=RANDBETWEEN (1,12)”,得到6个数,代表6个人的出生月份,完成一次模拟试验.选中A1、B1、C1、D1、E1、F1单元格,将鼠标指向右下角的黑点,按住鼠标左键拖动到第20行,相当于做20次重复试验. 统计其中有相同数的频率,得到事件A的概率的估计值.
点开用计算机模拟
下表是20次模拟试验的结果. 事件A发生了14次,事件A的概率估计值为0.70,与事件A的概率(约0.78)相差不大.
例2.在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
设事件A=“甲获得冠军”, B=“单局比赛甲胜”,则P(A)=0.6.用计算机产生1~5之间的随机数,当出现随机数1,2或3时,表示一局比赛甲获胜,其概率为0.6.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数.
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354
相当于做了20次重复试验.其中事件A发生了13次,对应的数组分别是423 123 423 114 332 152 342 512 125 432 334 151 314,用频率估计事件A的概率的近似值为
例3已知某运动员每次投篮命中的概率约为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569
683 431 257 393 027 556 488 730 113
537 989
据此估计,该运动员三次投篮恰有两次命中的概率为 ( )
A.0.35 B.0.25 C.0.20 D.0.15
【解析】选B.由题意知模拟三次投篮的结果,经随机模拟产生了20组随机数,在20组随机数中表示三次投篮恰有两次命中的有191,271,932,812,393,共5组随机数,所以所求概率为 = =0.25.
1. 随机模拟方法确定概率的估计值
2.随机数来求简单事件的概率
四、课堂小结(2分钟)
课堂素养达标
1.下列不能产生随机数的是 ( )
A.抛掷骰子试验
B.抛硬币
C.利用计算器
D.正方体的六个面上分别写有1,2,2,3,4,5,抛掷该正方体
【解析】选D.D项中,出现2的概率为 ,出现1,3,4,5的概率均是 ,故不能产生随机数.
五、当堂检测(14分钟)
2.随机模拟法产生的区间[0,1]上的实数 ( )
A.不是等可能的 B.0出现的机会少
C.1出现的机会少 D.是均匀分布的
【解析】选D.用随机模拟法产生的区间[0,1]上的实数是均匀分布的,每一个数产生的机会是均等的.
3.袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为 ( )
A. B. C. D.
.
【解析】选B.由随机模拟产生的随机数可知,直到第二次停止的有13,43,23,13,13,共5个基本事件,故所求的概率为P= = .
4.在用随机数(整数)模拟求“有4个男生和5个女生,从中选4个,求选出2个男生2个女生”的概率时,可让计算机产生1~9的随机整数,并用1~4代表男生,用5~9代表女生.因为是选出4个,所以每4个随机数作为一组.若得到的一组随机数为“4678”,则它代表的含义是________.
【解析】用1~4代表男生,5~9代表女生,4678表示一男三女.
答案:选出的4个人中,只有1个男生
高一数学第二册第十章:概率
10.3.2 随 机 模 拟
1.理解随机数的产生;
2.了解随机模拟方法确定概率的估计值;
3.会利用随机数来求简单事件的概率.
一、学习目标
二、问题导学
阅读教材255--257,回答下列问题:
思考:用频率估计概率,需要做大量的重复试验.有没有其他方法可以替代试验呢
随机模拟
随机数:例如我们要产生0~9之间的随机整数, 像彩票摇奖那样,把10个质地和大小相同的号码球放入摇奖器中,充分搅拌后摇出一个球,这个球上的号码就称为随机数.
伪随机数:计算器或计算机产生的随机数是按照确定的算法产生的数,具有周期性(周期很长),它们具有类似随机数的性质.因此,计算器或计算机产生的随机数不是真正的随机数,我们称它们为伪随机数
三、点拨精讲(25分钟)
1、随机模拟产生的原因:
用频率估计概率,需要做大量的重复试验,费时、费力,甚至难以实现.
2、随机模拟的方法:
利用计算器或计算软件产生随机数(根据不同的随机试验构建相应的随机数模拟试验)
又如,一个袋中装有2个红球和3个白球,这些球除颜色不同外没有其他差别. 对于从袋中摸出一个球的试验,我们可以让计算器或计算机产生取值于集合{1,2,3,4,5}的随机数,用1、2表示红球,用3、4、5表示白球. 这样不断产生1~5之间的整数随机数,相当于不断地做从袋中摸球的试验.
例如,对于抛掷一枚质地均匀硬币的试验,我们可以让计算器或计算机产生取值于集合{0,1} 的随机数,用0表示反面朝上,用1表示正面朝上.这样不断产生0、1两个随机数,相当于不断地做抛掷硬币的试验.
做整数随机模拟试验时,首先要确定随机数的范围,明确哪个数字代表哪个试验结果.
下表是用电子表格软件模拟上述摸球试验的结果,其中n为试验次数,nA为摸到红球的频数,fn(A)为摸到红球的频率.
n 10 20 50 100 150 200 250 300
nA 6 7 20 45 66 77 104 116
fn(A) 0.6 0.35 0.4 0.45 0.44 0.385 0.416 0.39
fn
n
10
20
50
100
150
200
250
300
利用随机模拟解决问题的方法为蒙特卡洛方法.
随机模拟方法是通过将一次试验所有可能发生的结果数字化,用计算机或计算器产生的随机数来替代每次试验的结果。其基本思想是用产生整数随机数的频率估计事件发生的概率.
例1 从你所在班级任意选出6名同学,调查他们的出生月份,假设
出生在一月,二月,…,十二月是等可能的.设事件A =“至少
有两人出生月份相同”,设计一种试验方法,模拟20次,估计
事件A发生的概率.
解:(法一随机数法)根据假设,每个人的出生月份在12个月中是等可能的,而且相互之间没有影响,所以观察6个人的出生月份可以看成可重复试验.
因此,可以构建如下有放回摸球试验进行模拟:在袋子中装入编号为1,2,…,12的12个球,这些球除编号外没有什么差别.有放回地随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验.如果这6个数中至少有2个相同,表示事件A发生了. 重复以上模拟试验20次,就可以统计出事件A发生的频率.
例1 从你所在班级任意选出6名同学,调查他们的出生月份,假设
出生在一月,二月,…,十二月是等可能的.设事件A =“至少
有两人出生月份相同”,设计一种试验方法,模拟20次,估计
事件A发生的概率.
(法二:计算机模拟,伪随机数)利用电子表格软件模拟试验. 在A1、B1、C1、D1、E1、F1单元格分别输人“=RANDBETWEEN (1,12)”,得到6个数,代表6个人的出生月份,完成一次模拟试验.选中A1、B1、C1、D1、E1、F1单元格,将鼠标指向右下角的黑点,按住鼠标左键拖动到第20行,相当于做20次重复试验. 统计其中有相同数的频率,得到事件A的概率的估计值.
点开用计算机模拟
下表是20次模拟试验的结果. 事件A发生了14次,事件A的概率估计值为0.70,与事件A的概率(约0.78)相差不大.
例2.在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
解:
设事件A=“甲获得冠军”, B=“单局比赛甲胜”,则P(A)=0.6.用计算机产生1~5之间的随机数,当出现随机数1,2或3时,表示一局比赛甲获胜,其概率为0.6.由于要比赛3局,所以每3个随机数为一组.例如,产生20组随机数.
423 123 423 344 114 453 525 332 152 342
534 443 512 541 125 432 334 151 314 354
相当于做了20次重复试验.其中事件A发生了13次,对应的数组分别是423 123 423 114 332 152 342 512 125 432 334 151 314,用频率估计事件A的概率的近似值为
例3已知某运动员每次投篮命中的概率约为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:
907 966 191 925 271 932 812 458 569
683 431 257 393 027 556 488 730 113
537 989
据此估计,该运动员三次投篮恰有两次命中的概率为 ( )
A.0.35 B.0.25 C.0.20 D.0.15
【解析】选B.由题意知模拟三次投篮的结果,经随机模拟产生了20组随机数,在20组随机数中表示三次投篮恰有两次命中的有191,271,932,812,393,共5组随机数,所以所求概率为 = =0.25.
1. 随机模拟方法确定概率的估计值
2.随机数来求简单事件的概率
四、课堂小结(2分钟)
课堂素养达标
1.下列不能产生随机数的是 ( )
A.抛掷骰子试验
B.抛硬币
C.利用计算器
D.正方体的六个面上分别写有1,2,2,3,4,5,抛掷该正方体
【解析】选D.D项中,出现2的概率为 ,出现1,3,4,5的概率均是 ,故不能产生随机数.
五、当堂检测(14分钟)
2.随机模拟法产生的区间[0,1]上的实数 ( )
A.不是等可能的 B.0出现的机会少
C.1出现的机会少 D.是均匀分布的
【解析】选D.用随机模拟法产生的区间[0,1]上的实数是均匀分布的,每一个数产生的机会是均等的.
3.袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为 ( )
A. B. C. D.
.
【解析】选B.由随机模拟产生的随机数可知,直到第二次停止的有13,43,23,13,13,共5个基本事件,故所求的概率为P= = .
4.在用随机数(整数)模拟求“有4个男生和5个女生,从中选4个,求选出2个男生2个女生”的概率时,可让计算机产生1~9的随机整数,并用1~4代表男生,用5~9代表女生.因为是选出4个,所以每4个随机数作为一组.若得到的一组随机数为“4678”,则它代表的含义是________.
【解析】用1~4代表男生,5~9代表女生,4678表示一男三女.
答案:选出的4个人中,只有1个男生
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
