六年级下册数学 第四单元 正比例和反比例练习 课件(20张PPT)
文档属性
| 名称 | 六年级下册数学 第四单元 正比例和反比例练习 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-11 19:10:58 | ||
图片预览







文档简介
(共20张PPT)
正比例和反比例练习
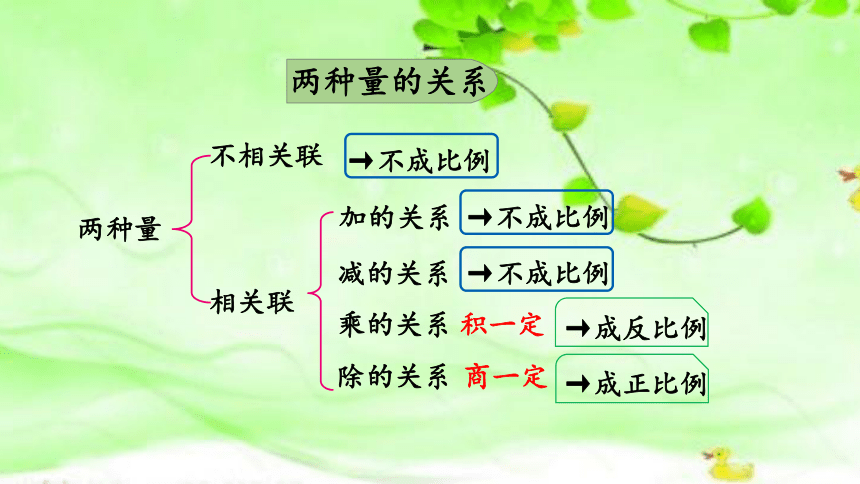
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
积一定
商一定
两种量的关系
→不成比例
→成反比例
→不成比例
→不成比例
→成正比例
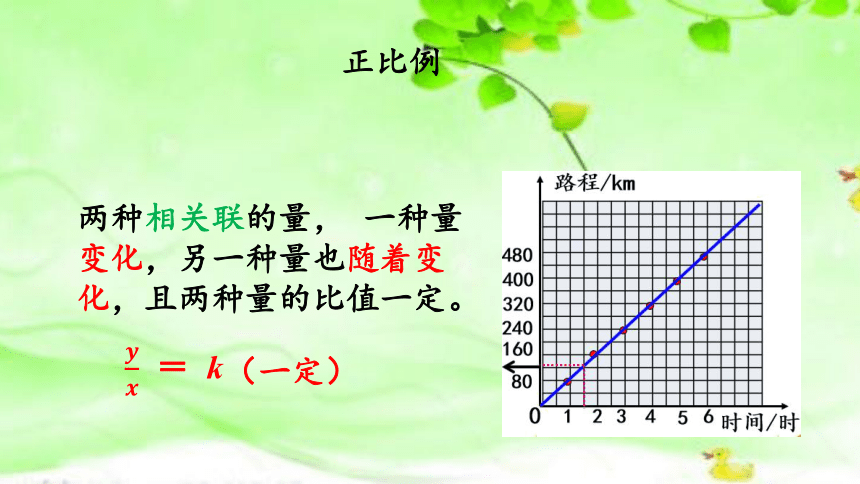
正比例
两种相关联的量, 一种量变化,另一种量也随着变化,且两种量的比值一定。
(一定)
= k
两种量成正比例关系要满足以下三个条件:
(1)必须是两种相关联的量
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的比值(也就是商)一定。
反比例
两种相关联的量,一种量变化,另一种量也随着变化,且两种量的乘积一定。
y
x
=k
(一定)
两种量成反比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的积一定。
相同点 不同点
正比例
反比例
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
都是两种相关联的量,一种量随着另一种量变化。
1.变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2.相关联的两个量相对应的两个数的比值(商)一定。
2.相关联的两个量相对应的两个数的乘积一定。
关系式:
3.关系式:
正、反比例的相同点和不同点
=
k
(一定)
(一定)
x
y =
k
小组讨论:正反比例的相同点和不同点分别是什么?
一看是不是( )。
二看是不是( )。
三看是不是( )或( )。
相关联
能变化
商一定
举手回答:你怎样判断两种量是否成正反比例关系:
积一定
下面各题中的两种量成正比例吗 成正比例的画“√”,不成
正比例的画“ ”。
(1)每小时织布的米数一定,织布的总米数与时间。( )
√
×
√
(2)人的身高与体重。 ( )
(3)《小学生天地》的单价一定,订阅费用与数量。( )
你能举出生活中反比例关系的例子吗?
路程=速度×时间
总数=分的人数×每人分的数量
路程一定,速度和时间成反比例关系。
总数一定,分的人数和每人分的数量成反比例关系。
有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成 比例关系。
xy=z
即xy的积一定,
(一定)
则xy成反比例。
xy=z
反
则zy成正比例。
正
则zx成正比例。
(2)当x一定时,z与y成 比例关系。
(一定),
=
x
(3)当y一定时,z与x成 比例关系。
xy=z
=
y
(一定),
正
判断下面每题中的两种量是不是成反比例,并说明理由。
因为
所以
每袋大米的质量和装的袋数成反比例。
每袋大米的质量×装的袋数=大米的总质量(一定)。
大米的总质量一定,
每袋大米的质量和装的袋数。
每天的平均用煤量和使用天数成反比例。
判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与每天的平均用煤量。
因为
每天的平均煤量×使用天数=这批煤的总量(一定)。
所以
两个量相关联。
积一定
因为每组的人数×组数=全班的人数(一定),
所以每组的人数和组数成反比例。
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
判断下面各题中的两种量是否成反比例关系,并说明理由。
(3)铺地的面积一定,方砖的边长和所需要的块数成反比例。
判断下面各题中的两种量是否成反比例关系,并说明理由。
边长ⅹ边长=方砖的面积
方砖的面积ⅹ所需块数=铺地的面积(一定)
铺地的面积一定,方砖的边长
和所需要的块数不成反比例。
边长ⅹ所需块数=
铺地面积
边长
边长不是定值, 也不是定值
铺地面积
边长
判断下面每题中的两种量是不是成反比例,并说明理由。
因为
所以
每袋大米的质量和装的袋数成反比例。
每袋大米的质量×装的袋数=大米的总质量(一定)。
大米的总质量一定,
每袋大米的质量和装的袋数。
年均开采量/亿吨 3 9 15 21 30 …
可开采年数/年 630 210 126 90 63 …
我国煤炭年均开采量与可开采年数之间的关系如下表。
表中的两种量是否成比例 如果成比例,请判断成什么比例。
宽/厘米 10 12 15
长/厘米
用240个边长是1厘米的小正方形摆成不同的长方形。
长与宽成反比例关系吗 为什么
因数 1 18
因数 18 1
乘积是18的两个因数之间的关系。
根据上表中的数据,在下图中描出各点,并连成一条曲线。
正比例和反比例练习
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
积一定
商一定
两种量的关系
→不成比例
→成反比例
→不成比例
→不成比例
→成正比例
正比例
两种相关联的量, 一种量变化,另一种量也随着变化,且两种量的比值一定。
(一定)
= k
两种量成正比例关系要满足以下三个条件:
(1)必须是两种相关联的量
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的比值(也就是商)一定。
反比例
两种相关联的量,一种量变化,另一种量也随着变化,且两种量的乘积一定。
y
x
=k
(一定)
两种量成反比例关系要满足以下三个条件:
(1)必须是两种相关联的量。
(2)一种量变化,另一种量也随着变化。
(3)两种量中相对应的两个数的积一定。
相同点 不同点
正比例
反比例
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
都是两种相关联的量,一种量随着另一种量变化。
1.变化的方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)。
2.相关联的两个量相对应的两个数的比值(商)一定。
2.相关联的两个量相对应的两个数的乘积一定。
关系式:
3.关系式:
正、反比例的相同点和不同点
=
k
(一定)
(一定)
x
y =
k
小组讨论:正反比例的相同点和不同点分别是什么?
一看是不是( )。
二看是不是( )。
三看是不是( )或( )。
相关联
能变化
商一定
举手回答:你怎样判断两种量是否成正反比例关系:
积一定
下面各题中的两种量成正比例吗 成正比例的画“√”,不成
正比例的画“ ”。
(1)每小时织布的米数一定,织布的总米数与时间。( )
√
×
√
(2)人的身高与体重。 ( )
(3)《小学生天地》的单价一定,订阅费用与数量。( )
你能举出生活中反比例关系的例子吗?
路程=速度×时间
总数=分的人数×每人分的数量
路程一定,速度和时间成反比例关系。
总数一定,分的人数和每人分的数量成反比例关系。
有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成 比例关系。
xy=z
即xy的积一定,
(一定)
则xy成反比例。
xy=z
反
则zy成正比例。
正
则zx成正比例。
(2)当x一定时,z与y成 比例关系。
(一定),
=
x
(3)当y一定时,z与x成 比例关系。
xy=z
=
y
(一定),
正
判断下面每题中的两种量是不是成反比例,并说明理由。
因为
所以
每袋大米的质量和装的袋数成反比例。
每袋大米的质量×装的袋数=大米的总质量(一定)。
大米的总质量一定,
每袋大米的质量和装的袋数。
每天的平均用煤量和使用天数成反比例。
判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与每天的平均用煤量。
因为
每天的平均煤量×使用天数=这批煤的总量(一定)。
所以
两个量相关联。
积一定
因为每组的人数×组数=全班的人数(一定),
所以每组的人数和组数成反比例。
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
判断下面各题中的两种量是否成反比例关系,并说明理由。
(3)铺地的面积一定,方砖的边长和所需要的块数成反比例。
判断下面各题中的两种量是否成反比例关系,并说明理由。
边长ⅹ边长=方砖的面积
方砖的面积ⅹ所需块数=铺地的面积(一定)
铺地的面积一定,方砖的边长
和所需要的块数不成反比例。
边长ⅹ所需块数=
铺地面积
边长
边长不是定值, 也不是定值
铺地面积
边长
判断下面每题中的两种量是不是成反比例,并说明理由。
因为
所以
每袋大米的质量和装的袋数成反比例。
每袋大米的质量×装的袋数=大米的总质量(一定)。
大米的总质量一定,
每袋大米的质量和装的袋数。
年均开采量/亿吨 3 9 15 21 30 …
可开采年数/年 630 210 126 90 63 …
我国煤炭年均开采量与可开采年数之间的关系如下表。
表中的两种量是否成比例 如果成比例,请判断成什么比例。
宽/厘米 10 12 15
长/厘米
用240个边长是1厘米的小正方形摆成不同的长方形。
长与宽成反比例关系吗 为什么
因数 1 18
因数 18 1
乘积是18的两个因数之间的关系。
根据上表中的数据,在下图中描出各点,并连成一条曲线。
