7.1 条件概率与全概率公式(共38张PPT)
文档属性
| 名称 | 7.1 条件概率与全概率公式(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
条件概率
学习目标
理解条件概率的定义
掌握条件概率的计算方法
利用条件概率公式解决一些简单的实际问题
教学重点
教学难点
条件概率的概念,条件概率公式的简单应用
正确理解条件概率公式,并能灵活运用条件概率公式解决简单实际问题
我们知道求事件的概率有加法公式:
那么怎么求A与B的积事件AB呢
3.若AB为不可能事件,则说事件A与B互斥.
积事件
和事件
探究
三张奖券中只有一张能中奖,现分别由3名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两位小?
“最后一名同学抽到中奖奖券”为事件B
思考1
如果已经知道第一名同学没有中奖,那么最后一名同学中奖的概率是多少?
知道第一名同学的结果会影响最后一名同学中奖的概率吗?
“第一名同学没有抽到中奖奖券”为事件A
“最后一名同学抽到中奖奖券”为事件B
第一名同学没有抽到中奖奖券的条件下,最后一名 同学抽到中奖奖券的概率记为P(B|A)
已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
思考2
对于上面的事件A和事件B,P(B|A)与它们的概率有什么关系呢?
P(B |A)相当于把A看作新的
基本事件空间求A∩B发生的
概率
条件概率定义
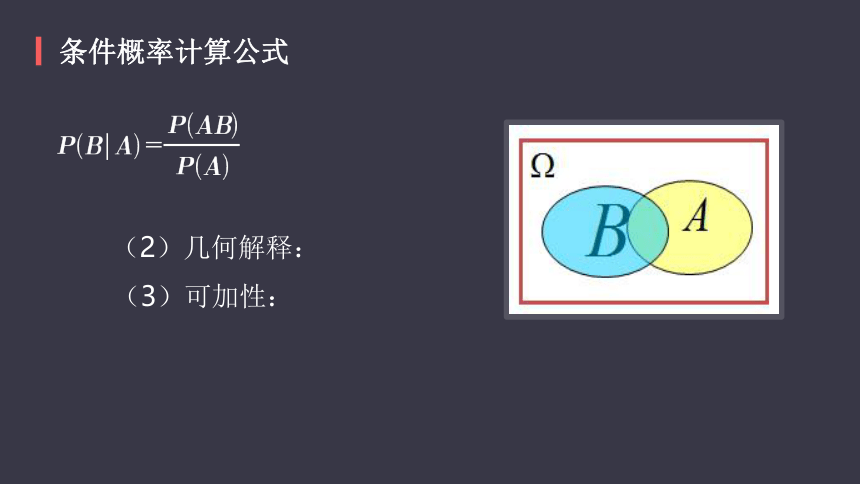
条件概率计算公式
(2)几何解释:
(3)可加性:
条件概率
基本概念
概率 P(B|A)与P(AB)的区别与联系
条件概率;
条件概率的计算。
条件概率
例题
在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第一次抽到几何题的条件下,第2次抽打几何体的概率.
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
例题
已知3张奖券中只有1张有奖,甲、乙、丙3名同学一次无放回的各抽一张,他们中奖的概率与抽奖的次序有关吗
拓展:事实上,在抽奖问题上,无论是放回还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例题
储蓄卡的密码由6位数字组成某人在银行自勇取款机上取钱时,忘记了密码的最后1位数字,求
(1)任意按最后1位数字,不超过2次就按对的概率
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率
例题
抛掷一颗骰子,观察出现的点数
B={出现的点数是奇数}={1,3,5}
A={出现的点数不超过3}={1,2,3}
若已知出现的点数不超过3,求出现的点数是奇数的概率
解:即事件 A 已发生,求事件 B 的概率也就是求:P(B|A)
A B 都发生,但样本空间缩小到只包含A的样本点
例题
设 100 件产品中有 70 件一等品,25 件二等品,规定一、二等品为合格品.从中任取1 件,求 (1) 取得一等品的概率;(2) 已知取得的是合格品,求它是一等品的概率.
设B表示取得一等品,A表示取得合格品,则
解:
条件概率的计算
1.从一副不含大小王的52张扑克牌中,每次随机从中取出1张扑克牌,抽出的牌不再放回.已知第1次抽到A牌 ,求第2 次抽到A牌的概率.
【解答】
条件概率的计算
条件概率的计算
3.袋子中有10个大小相同的小球,其中7个白球,3个黑球.每次从袋子中随机摸出1个球,摸出的球不再放回,求:
(1)在第1次摸到白球的条件下,第2次摸到白球的概率;
(2)两次都摸到白球的概率.
全概率公式定义
我们称上面的公式为全概率公式.
例题
某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第二天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率.
例题
有3台车床加工同一型号的零件,第1台加工的次品率为6%。第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别站总数的25%,30%,45%.
(1)人去一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算他是第i(i=1,2,3)台车床加工的概率.
例题
在数字通信中,信号是由数字0和1 组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接受为1或0.已知发送信号时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.955和0.05.假设发送信号0和1是等可能的.
(1)分别求接收的信号为0和1的概率;
(2)已知接收的信号为0,求发送的信号是1的概率.
全概率公式
1.现有12 道四选一的单选题,学生张君对其中的9道题有思路,3道题完全没有思路.有思路的题作对的概率为0.9,没有思路的题也只好猜一个答案,才对答案的概率为0.25.张君从这12道题中随机选择1题,求他做对该题的概率.
全概率公式
2.两种规格的产品,第一批占40%,次品率为5%;第二批占60%,次品率为4%.将两批产品混合,从这混合产品中任取1件.
(1)求这件产品是合格品的概率;
(2)已知取到的是合格品,求它取自第一批产品的概率.
拓展
贝叶斯公式是由英国数学家贝叶斯发现的,它用来描述两个条件概率之间的关系.
1.为了研究不同性别学生患色盲的比例,调查了某学校2000名学生,数据如下表显示.
课后习题
从这2000人中随机选择1个人.
(1)已知选到的是男生,求他患色盲的概率;
(2)已知选到的学生患色盲,求他是男生的概率.
男
女
合计
色盲
非色盲
合计
60
2
62
1140
798
1938
1200
800
2000
课后习题
P(B)>P(C)
课后习题
0.3
课后习题
4.甲和乙两个箱子中各装有10个球,其中甲箱中有5个红球、5个白球,乙箱中有8个红球、2个白球.掷一枚质地均匀的骰子,如果点数为1或2 ,从甲箱子随机摸出1个球;如果点数为3,4,5,6,从乙箱子中随机摸出1个球.求摸到红球的概率.
课后习题
5.在A,B,C三个地区爆发了流感,这三个地区分别有6%,5%,4%的人患了流感.假设这三个地区的人口数的比为5:7:8,现从这三个地区任意选取一个人.
(1)求这个人患流感的概率;
(2)如果此人患流感,求此人选自A地区的概率.
课后习题
6.一批产品共有100件,其中5件为不合格品.收货方从中不放回得随机抽取产品进行检验,并按照以下规则判断是否接受 这批产品:如果抽检的第1件产品不合格,则拒绝整批产品;如果抽检的第1件产品合格,则再抽取1件,如果抽取的第2件产品合格,则接受整批产品,否则拒绝整批产品.求这批产品被拒绝的概率.
课后习题
7.在孟德尔豌豆试验中,子二代的基因型为DD,Dd,dd,其中D为显性基因,d为隐性基因,且这三种基因型的比为1:2:1.若果在子二代中任意选取2颗豌豆作为父本杂交,那么子三代中基因型为dd的概率是多大?
总结
1.条件概率的定义:
2.条件概率的性质:
3.条件概率的求法:
条件概率
学习目标
理解条件概率的定义
掌握条件概率的计算方法
利用条件概率公式解决一些简单的实际问题
教学重点
教学难点
条件概率的概念,条件概率公式的简单应用
正确理解条件概率公式,并能灵活运用条件概率公式解决简单实际问题
我们知道求事件的概率有加法公式:
那么怎么求A与B的积事件AB呢
3.若AB为不可能事件,则说事件A与B互斥.
积事件
和事件
探究
三张奖券中只有一张能中奖,现分别由3名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两位小?
“最后一名同学抽到中奖奖券”为事件B
思考1
如果已经知道第一名同学没有中奖,那么最后一名同学中奖的概率是多少?
知道第一名同学的结果会影响最后一名同学中奖的概率吗?
“第一名同学没有抽到中奖奖券”为事件A
“最后一名同学抽到中奖奖券”为事件B
第一名同学没有抽到中奖奖券的条件下,最后一名 同学抽到中奖奖券的概率记为P(B|A)
已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
思考2
对于上面的事件A和事件B,P(B|A)与它们的概率有什么关系呢?
P(B |A)相当于把A看作新的
基本事件空间求A∩B发生的
概率
条件概率定义
条件概率计算公式
(2)几何解释:
(3)可加性:
条件概率
基本概念
概率 P(B|A)与P(AB)的区别与联系
条件概率;
条件概率的计算。
条件概率
例题
在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第一次抽到几何题的条件下,第2次抽打几何体的概率.
解法1:设A=“第1次抽到代数题”,B=“第2次抽到几何题”.
例题
已知3张奖券中只有1张有奖,甲、乙、丙3名同学一次无放回的各抽一张,他们中奖的概率与抽奖的次序有关吗
拓展:事实上,在抽奖问题上,无论是放回还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例题
储蓄卡的密码由6位数字组成某人在银行自勇取款机上取钱时,忘记了密码的最后1位数字,求
(1)任意按最后1位数字,不超过2次就按对的概率
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率
例题
抛掷一颗骰子,观察出现的点数
B={出现的点数是奇数}={1,3,5}
A={出现的点数不超过3}={1,2,3}
若已知出现的点数不超过3,求出现的点数是奇数的概率
解:即事件 A 已发生,求事件 B 的概率也就是求:P(B|A)
A B 都发生,但样本空间缩小到只包含A的样本点
例题
设 100 件产品中有 70 件一等品,25 件二等品,规定一、二等品为合格品.从中任取1 件,求 (1) 取得一等品的概率;(2) 已知取得的是合格品,求它是一等品的概率.
设B表示取得一等品,A表示取得合格品,则
解:
条件概率的计算
1.从一副不含大小王的52张扑克牌中,每次随机从中取出1张扑克牌,抽出的牌不再放回.已知第1次抽到A牌 ,求第2 次抽到A牌的概率.
【解答】
条件概率的计算
条件概率的计算
3.袋子中有10个大小相同的小球,其中7个白球,3个黑球.每次从袋子中随机摸出1个球,摸出的球不再放回,求:
(1)在第1次摸到白球的条件下,第2次摸到白球的概率;
(2)两次都摸到白球的概率.
全概率公式定义
我们称上面的公式为全概率公式.
例题
某学校有A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐.如果第1天去A餐厅,那么第二天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8.计算王同学第2天去A餐厅用餐的概率.
例题
有3台车床加工同一型号的零件,第1台加工的次品率为6%。第2,3台加工的次品率均为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别站总数的25%,30%,45%.
(1)人去一个零件,计算它是次品的概率;
(2)如果取到的零件是次品,计算他是第i(i=1,2,3)台车床加工的概率.
例题
在数字通信中,信号是由数字0和1 组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接受为1或0.已知发送信号时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.955和0.05.假设发送信号0和1是等可能的.
(1)分别求接收的信号为0和1的概率;
(2)已知接收的信号为0,求发送的信号是1的概率.
全概率公式
1.现有12 道四选一的单选题,学生张君对其中的9道题有思路,3道题完全没有思路.有思路的题作对的概率为0.9,没有思路的题也只好猜一个答案,才对答案的概率为0.25.张君从这12道题中随机选择1题,求他做对该题的概率.
全概率公式
2.两种规格的产品,第一批占40%,次品率为5%;第二批占60%,次品率为4%.将两批产品混合,从这混合产品中任取1件.
(1)求这件产品是合格品的概率;
(2)已知取到的是合格品,求它取自第一批产品的概率.
拓展
贝叶斯公式是由英国数学家贝叶斯发现的,它用来描述两个条件概率之间的关系.
1.为了研究不同性别学生患色盲的比例,调查了某学校2000名学生,数据如下表显示.
课后习题
从这2000人中随机选择1个人.
(1)已知选到的是男生,求他患色盲的概率;
(2)已知选到的学生患色盲,求他是男生的概率.
男
女
合计
色盲
非色盲
合计
60
2
62
1140
798
1938
1200
800
2000
课后习题
P(B)>P(C)
课后习题
0.3
课后习题
4.甲和乙两个箱子中各装有10个球,其中甲箱中有5个红球、5个白球,乙箱中有8个红球、2个白球.掷一枚质地均匀的骰子,如果点数为1或2 ,从甲箱子随机摸出1个球;如果点数为3,4,5,6,从乙箱子中随机摸出1个球.求摸到红球的概率.
课后习题
5.在A,B,C三个地区爆发了流感,这三个地区分别有6%,5%,4%的人患了流感.假设这三个地区的人口数的比为5:7:8,现从这三个地区任意选取一个人.
(1)求这个人患流感的概率;
(2)如果此人患流感,求此人选自A地区的概率.
课后习题
6.一批产品共有100件,其中5件为不合格品.收货方从中不放回得随机抽取产品进行检验,并按照以下规则判断是否接受 这批产品:如果抽检的第1件产品不合格,则拒绝整批产品;如果抽检的第1件产品合格,则再抽取1件,如果抽取的第2件产品合格,则接受整批产品,否则拒绝整批产品.求这批产品被拒绝的概率.
课后习题
7.在孟德尔豌豆试验中,子二代的基因型为DD,Dd,dd,其中D为显性基因,d为隐性基因,且这三种基因型的比为1:2:1.若果在子二代中任意选取2颗豌豆作为父本杂交,那么子三代中基因型为dd的概率是多大?
总结
1.条件概率的定义:
2.条件概率的性质:
3.条件概率的求法:
