7.5 正态分布(共35张PPT)
文档属性
| 名称 | 7.5 正态分布(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 16:27:24 | ||
图片预览










文档简介
(共35张PPT)
正态分布
利用实际问题的直方图,了解正态分布曲线的特点及曲线所表示的意义.
会用正态分布去解决实际问题。
了解变量落在区间(μ-σ,μ+σ],(μ-2σ,μ+2o],(μ-3σ, μ+ 3σ]的概率大小.
学习目标
理解并掌握正态分布曲线的图象性质
掌握在特定区间概率的求法
掌握3σ原则
教学重难点
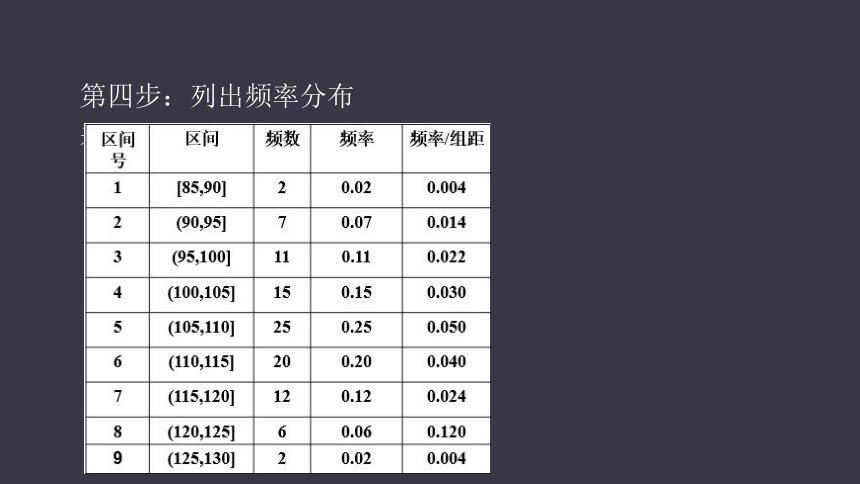
96,114,128,106,89,97,103,114,109,101,106,104,97,93,117,108,104,113,94,108,87,112,109,117,102,97,113,109,89,101,105,104,99,101,117,108,104,97,94,99,103,112,98,85,106,89,97,103,125,109,101,106,124,97,109,117,108,104,104,94,108,96,106,85,106,89,99,106,112,103,129,89,96,123,85,106,102,97,103,114,109,101,106,115,97,93,117,108,104,112,113,108,96,98,85,106,89,97,103,114
从学生中随机抽取出100个人做IQ测试,测试结果如下:
频率分布
直方图
第一步:求极差 ;129-85=44
第二步:确定组数,组距;44/5=8.8
第三步:将数据分9组;[85,90],(90,95], …… ,(125,130]
第四步:列出频率分布表
第五步:画出频率分布直方图
若数据无限增多且组距无限缩小,那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线,我们称这样的曲线为密度曲线.
密度曲线
高尔顿板
以球槽的编号为横坐标
以小球落入各个球槽内的频率值为纵坐标
频率分布直方图
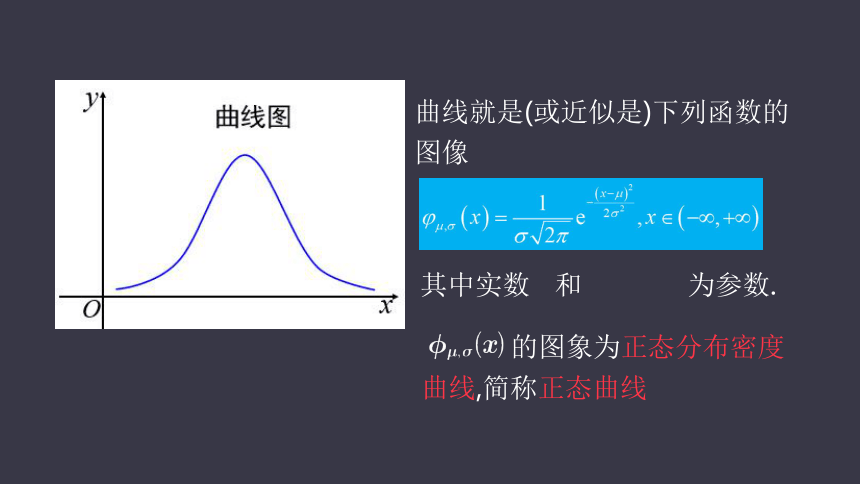
曲线就是(或近似是)下列函数的图像
其中实数 和 为参数.
的图象为正态分布密度曲线,简称正态曲线
正态分布的概念;
利用正态分布的意义,算概率。
正态分布
正态曲线的定义
这条曲线就是或近似地是以下函数的图象:
函数式中的实数μ、σ(σ>0)是参数,分别表示总体的平均数与标准差,称函数的图象称为正态分布密度曲线,简称正态曲线.
正态分布的定义
如果对于任何实数 ,随机变量X满足:
则称X 服从正态分布. 正态分布由参数μ、σ唯一确定.正态分布记作 .其图象称为正态曲线.
如果随机变量X服从正态分布,则记作
参数μ是随机变量X的均值.
参数σ是随机变量X的标准差
μ的意义
总体平均数反映总体随机变量的平均水平
σ的意义
总体标准差反映总体随机变量的集中与分散的程度
正态曲线的定义
总体平均数反映总体随机变量的平均水平
总体标准差反映总体随机变量的集中与分散的程度
正态总体的函数表示式
当μ= 0,σ=1时
标准正态总体
正态总体的函数表示式
1、当f(x)=_____时,函数值为最大。
2、f(x)的值域为________________。
3、f(x)的图像关于__________对称。
4、当x∈____________时f(x)为增函数;
当x∈____________时f(x)为减函数;
μ
(-∞,μ]
(μ,+∞)
x=μ
正态总体的函数表示式
曲线在x轴的上方,与x轴不相交
曲线是单峰的,它关于直线x=μ对称
曲线在x=μ处达到峰值(最高点)
曲线与x轴之间的面积为1
正态总体的函数表示式
当 x<μ时,曲线上升;当x>μ时,曲线下降.
并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
当σ 一定时,正态曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移;
特殊区间的概率
μ-a
μ+a
x=μ
特殊区间的概率
上述结果可用下图表示
3σ原则
正态总体几乎总取值于区间 之内,而在此区间以外取值的概率只有0.26%,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布 的随机变量只取 之间的值,并称为3σ原则.
李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min, 样本方差为36;骑自行车平均用时34 min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1) 估计X, Y的分布中的参数; .
(2) 根据(1) 中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有38 min可用,李明应选择哪种交通工具 如果某天只有34 min可用,又应该选择哪种交通工具 请说明理由.
例题
解: (1) 随机变量X的样本均值为30,样本标准差为6;随机变量Y的样本均值为34,样本标准差为2.用样本均值估计参数μ,用样本标准差估计参数σ,可以得到
(2)X和Y的分布密度曲线如图7.5-7所示.
(3)应选择在给定时间内不迟到的概率大的交通工具.由图7.5-7可知:
P(X≤38)P(X≤34) P(X≤38)P(X≤34)
所以,如果有38 min可用,哪么骑自行车不迟到的概 率大,应选择骑自行车:如果只有34 min可用,那么坐公交车不迟到的概事大。应选择坐公交车.
假设 可以证明:对给定的 是一个只与k有关的定值。特别地。
P(μ-σ≤X≤μ+σ)≈0 682 7。
P(μ-2σ≤X≤μ+2σ)≈0.954 5,
P(u-3σ≤X≤μ+3σ)≈0.997 3.
上述结果可用图7.5-8表示
由此看到,尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间[μ-3, μ+30]内,而在此区间以外取值的概率大约只有0, 002 7 .通常认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布 的随机变量X只取[μ- 3σ, μ+3σ]中的值,这在统计学中称为3σ原则.
1.设随机变量X~N(0,1), 则X的密度函数为
_____________________________________,P(X≤0)=__________,P( |X |≤1)=___________ ,P(X≤1)=__________,P(X>1)=__________. (精确到0. 0001.)
0.5
0.6826
0.8413
0.1587
练1
练2
A.
B.
C.
D.
【解答】
D
练3
A.
B.
C.
D.
【解答】
B
【解答】
练4
对某地区数学考试成绩的数据分析,男生成绩X服从正态分布 ,女生成绩Y服从正态分布 .请你从不同角度比较男、女生的考试成绩.
课后习题
解答:略
解答:
(1)0.6826
(2)0.1587
(3)0.1587
课后习题
课后习题
3.若 ,则X位于区城[μ, μ+σ]内的概率是多少
0.3143
课后习题
袋装食盐标准质量为400 g,规定误差的绝对值不超过4 g就认为合格.假设误差服从正态分布,随机抽取100袋食盐,误差的样本均值为0,样本方差为4.请你估计这批袋装食盐的合格率.
解答:
略
总结
正态总体函数解析式:
正态曲线
正态曲线的性质
曲线在x轴的上方,与x轴不相交
曲线关于直线x=μ对称
曲线在x=μ时位于最高点.
当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以轴为渐近线,向它无限靠近.
当μ一定时,曲线的形状由σ确定 .σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
总结
正态分布
利用实际问题的直方图,了解正态分布曲线的特点及曲线所表示的意义.
会用正态分布去解决实际问题。
了解变量落在区间(μ-σ,μ+σ],(μ-2σ,μ+2o],(μ-3σ, μ+ 3σ]的概率大小.
学习目标
理解并掌握正态分布曲线的图象性质
掌握在特定区间概率的求法
掌握3σ原则
教学重难点
96,114,128,106,89,97,103,114,109,101,106,104,97,93,117,108,104,113,94,108,87,112,109,117,102,97,113,109,89,101,105,104,99,101,117,108,104,97,94,99,103,112,98,85,106,89,97,103,125,109,101,106,124,97,109,117,108,104,104,94,108,96,106,85,106,89,99,106,112,103,129,89,96,123,85,106,102,97,103,114,109,101,106,115,97,93,117,108,104,112,113,108,96,98,85,106,89,97,103,114
从学生中随机抽取出100个人做IQ测试,测试结果如下:
频率分布
直方图
第一步:求极差 ;129-85=44
第二步:确定组数,组距;44/5=8.8
第三步:将数据分9组;[85,90],(90,95], …… ,(125,130]
第四步:列出频率分布表
第五步:画出频率分布直方图
若数据无限增多且组距无限缩小,那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线,我们称这样的曲线为密度曲线.
密度曲线
高尔顿板
以球槽的编号为横坐标
以小球落入各个球槽内的频率值为纵坐标
频率分布直方图
曲线就是(或近似是)下列函数的图像
其中实数 和 为参数.
的图象为正态分布密度曲线,简称正态曲线
正态分布的概念;
利用正态分布的意义,算概率。
正态分布
正态曲线的定义
这条曲线就是或近似地是以下函数的图象:
函数式中的实数μ、σ(σ>0)是参数,分别表示总体的平均数与标准差,称函数的图象称为正态分布密度曲线,简称正态曲线.
正态分布的定义
如果对于任何实数 ,随机变量X满足:
则称X 服从正态分布. 正态分布由参数μ、σ唯一确定.正态分布记作 .其图象称为正态曲线.
如果随机变量X服从正态分布,则记作
参数μ是随机变量X的均值.
参数σ是随机变量X的标准差
μ的意义
总体平均数反映总体随机变量的平均水平
σ的意义
总体标准差反映总体随机变量的集中与分散的程度
正态曲线的定义
总体平均数反映总体随机变量的平均水平
总体标准差反映总体随机变量的集中与分散的程度
正态总体的函数表示式
当μ= 0,σ=1时
标准正态总体
正态总体的函数表示式
1、当f(x)=_____时,函数值为最大。
2、f(x)的值域为________________。
3、f(x)的图像关于__________对称。
4、当x∈____________时f(x)为增函数;
当x∈____________时f(x)为减函数;
μ
(-∞,μ]
(μ,+∞)
x=μ
正态总体的函数表示式
曲线在x轴的上方,与x轴不相交
曲线是单峰的,它关于直线x=μ对称
曲线在x=μ处达到峰值(最高点)
曲线与x轴之间的面积为1
正态总体的函数表示式
当 x<μ时,曲线上升;当x>μ时,曲线下降.
并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近.
当σ 一定时,正态曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移;
特殊区间的概率
μ-a
μ+a
x=μ
特殊区间的概率
上述结果可用下图表示
3σ原则
正态总体几乎总取值于区间 之内,而在此区间以外取值的概率只有0.26%,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布 的随机变量只取 之间的值,并称为3σ原则.
李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30 min, 样本方差为36;骑自行车平均用时34 min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1) 估计X, Y的分布中的参数; .
(2) 根据(1) 中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
(3)如果某天有38 min可用,李明应选择哪种交通工具 如果某天只有34 min可用,又应该选择哪种交通工具 请说明理由.
例题
解: (1) 随机变量X的样本均值为30,样本标准差为6;随机变量Y的样本均值为34,样本标准差为2.用样本均值估计参数μ,用样本标准差估计参数σ,可以得到
(2)X和Y的分布密度曲线如图7.5-7所示.
(3)应选择在给定时间内不迟到的概率大的交通工具.由图7.5-7可知:
P(X≤38)P(X≤34) P(X≤38)P(X≤34)
所以,如果有38 min可用,哪么骑自行车不迟到的概 率大,应选择骑自行车:如果只有34 min可用,那么坐公交车不迟到的概事大。应选择坐公交车.
假设 可以证明:对给定的 是一个只与k有关的定值。特别地。
P(μ-σ≤X≤μ+σ)≈0 682 7。
P(μ-2σ≤X≤μ+2σ)≈0.954 5,
P(u-3σ≤X≤μ+3σ)≈0.997 3.
上述结果可用图7.5-8表示
由此看到,尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间[μ-3, μ+30]内,而在此区间以外取值的概率大约只有0, 002 7 .通常认为这种情况几乎不可能发生.
在实际应用中,通常认为服从于正态分布 的随机变量X只取[μ- 3σ, μ+3σ]中的值,这在统计学中称为3σ原则.
1.设随机变量X~N(0,1), 则X的密度函数为
_____________________________________,P(X≤0)=__________,P( |X |≤1)=___________ ,P(X≤1)=__________,P(X>1)=__________. (精确到0. 0001.)
0.5
0.6826
0.8413
0.1587
练1
练2
A.
B.
C.
D.
【解答】
D
练3
A.
B.
C.
D.
【解答】
B
【解答】
练4
对某地区数学考试成绩的数据分析,男生成绩X服从正态分布 ,女生成绩Y服从正态分布 .请你从不同角度比较男、女生的考试成绩.
课后习题
解答:略
解答:
(1)0.6826
(2)0.1587
(3)0.1587
课后习题
课后习题
3.若 ,则X位于区城[μ, μ+σ]内的概率是多少
0.3143
课后习题
袋装食盐标准质量为400 g,规定误差的绝对值不超过4 g就认为合格.假设误差服从正态分布,随机抽取100袋食盐,误差的样本均值为0,样本方差为4.请你估计这批袋装食盐的合格率.
解答:
略
总结
正态总体函数解析式:
正态曲线
正态曲线的性质
曲线在x轴的上方,与x轴不相交
曲线关于直线x=μ对称
曲线在x=μ时位于最高点.
当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以轴为渐近线,向它无限靠近.
当μ一定时,曲线的形状由σ确定 .σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
总结
