《平均变化率》课件

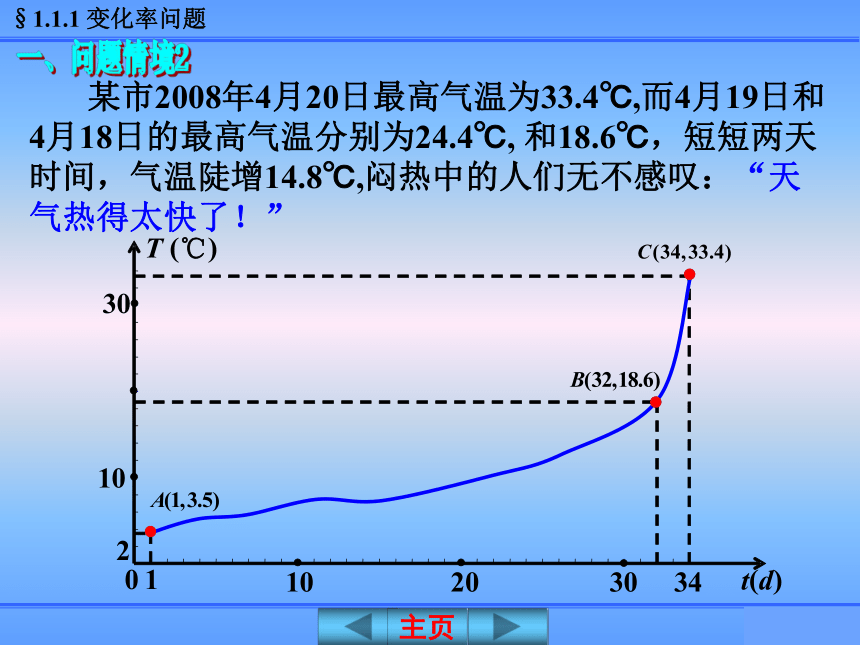
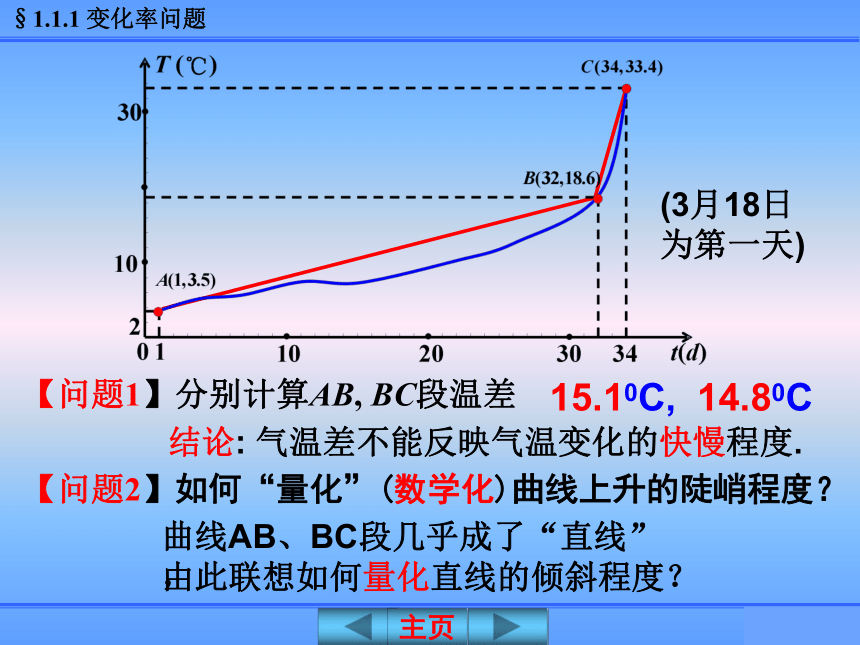
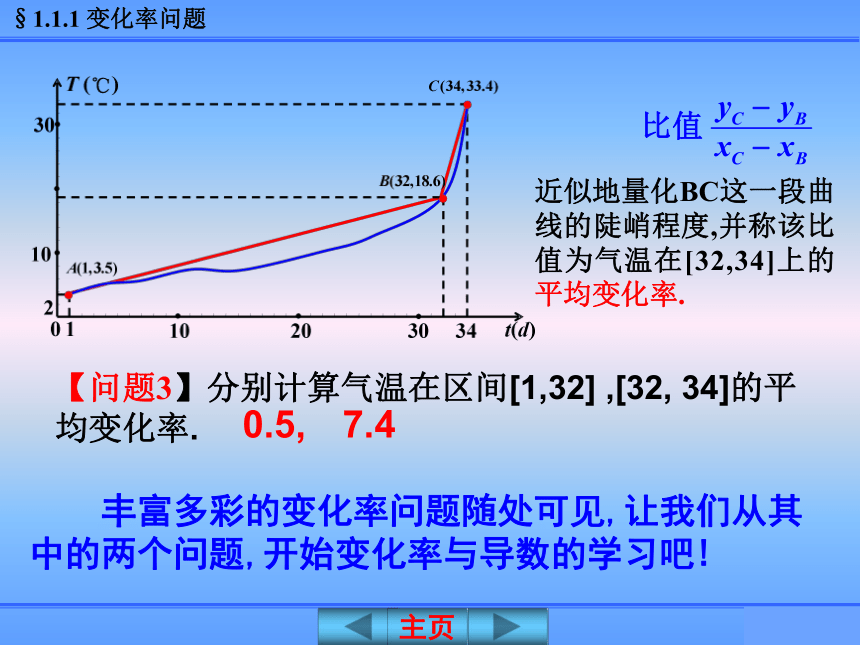
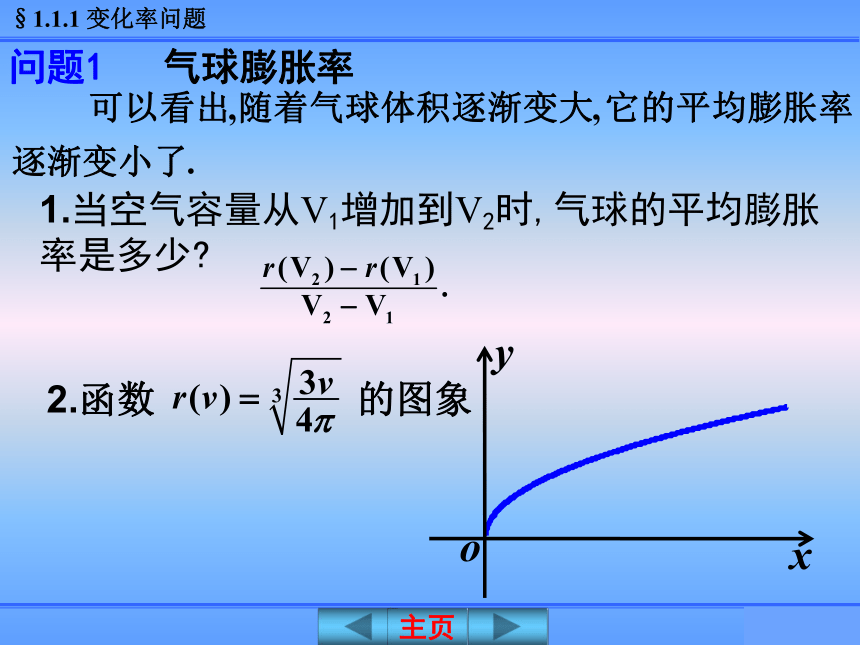
课件28张PPT。1.1.1 平 均 变 化 率人教A版选修2-2《导数及其应用》变化率与导数 　 某市2008年4月20日最高气温为33.4℃,而4月19日和4月18日的最高气温分别为24.4℃, 和18.6℃，短短两天时间，气温陡增14.8℃,闷热中的人们无不感叹：“天气热得太快了！”一、问题情境2203410t(d)0121030T (℃)30(3月18日为第一天)【问题1】分别计算AB, BC段温差15.10C,14.80C结论: 气温差不能反映气温变化的快慢程度.【问题2】如何“量化”(数学化)曲线上升的陡峭程度？由此联想如何量化直线的倾斜程度？曲线AB、BC段几乎成了“直线”，【问题3】分别计算气温在区间[1,32] ,[32, 34]的平均变化率.近似地量化BC这一段曲线的陡峭程度,并称该比值为气温在[32,34]上的平均变化率.0.5,7.4 丰富多彩的变化率问题随处可见,让我们从其中的两个问题,开始变化率与导数的学习吧!问题1 气球膨胀率二、建构数学问题1 气球膨胀率问题1 气球膨胀率气球半径增加了 气球的平均膨胀率为 当空气容量V从0增加到1L时，气球半径增加了多少？气球的平均膨胀率为多少？ 类似地，当空气容量V从1L增加到2L时，气球半径增加了多少？气球的平均膨胀率为多少？气球半径增加了 气球的平均膨胀率为 1.当空气容量从V1增加到V2时,气球的平均膨胀率是多少? 问题1 气球膨胀率2.函数 的图象问题2 高台跳水问题2 高台跳水 【探究】计算运动员在 这段时间里的平均速度，并思考下面的问题：(1)运动员在 这段时间里的平均速度为(2) 用平均速度不能精确描述运动员的运动状态．但实际情况是运动员仍然运动, 并非静止.1.平均变化率的定义二、建构数学(1)自变量的改变量(２)函数值的改变量(３)平均变化率的记法曲线的陡峭程度是平均变化率的“视觉化”(1)平均变化率是曲线陡峭程度的“数量化”，(2)用平均变化率量化一段曲线的陡峭程度是“粗糙不精确的”，但应注意当x2-x1很小时，这种量化便由“粗糙”逼近“精确”.D练一练 求函数y = f(x)在区间[x1,x2]上的平均变化率的步骤：(1)求自变量的增量 (2)求函数的增量 (3)求平均变化率 ?作差 ?作商思 考：三、数学运用例 【1】练一练【2】例2．已知函数f(x)=x2, 分别计算f(x)在下列区间上的平均变化率： 三、数学运用问题(1)求函数在[1, a] (a>1)上的平均变化率；例2引申： 已知函数f(x)=x2.平均变化率为 a+1平均变化率趋近于2问题(2)当a趋近于1时，函数在[1, a] 上的平均变化率有何趋势？探索：一次函数f(x)=kx+b在区间[m,n]上的平均变化率有何特点？结论：一次函数f(x)=kx+b在区间[m, n] 上的平均变化率就等于k.例3.某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率；由此你能得到什么结论？结论：该婴儿从出生到第3个月体重增加的速度比第6个月到第12个月体重增加的速度要快.36126.53.58.611W(kg)T(月)解:前3个月体重的平均变化率 第6个月到第12个月体重的平均变化率 【变式1】甲、乙两人跑步,路程与时间关系如图1及百米赛跑路程与时间关系分别如图2所示,试问：
(1)在这一段时间内甲、乙两人哪一个跑的较快？
(2)甲、乙两人百米赛跑，问快到终点时,谁跑的较快？图1甲乙路程图2甲乙路程 【变式2】向高为H的水瓶中注水,注满为止,如果注水量 y 与水深 x 的函数关系的图像如图所示,那么水瓶的形状 ( )H练一练问题1：本节课你学到了什么？
①函数的平均变化率的概念；
②利用平均变化率来分析解决实际问题问题2.解决平均变化率问题需要注意什么？
① 分清所求平均变化率类型(即什么对象的平均变化率)
② 两种处理手段：(1)看图(2)计算 问题3.本节课体现了哪些数学思想方法？
①数形结合的思想方法
②从特殊到一般、从具体到抽象的推理方法 平均变化率是曲线陡峭程度的“数量化”，是一种粗略的刻画--------导数五、回顾反思 美国康乃大学曾经做过一个有名的“青蛙试验”.试验人员把一只健壮的青蛙投入热水锅中，青蛙马上就感到了危险,拼命一纵便跳出了锅子.试验人员又把该青蛙投入冷水锅中,然后开始慢慢加热水锅.刚开始,青蛙自然悠哉游哉,毫无戒备.一段时间以后,锅里水的温度逐渐升高,而青蛙在缓慢的水温变化中却没有感到危险,最后,一只活蹦乱跳的健壮的青蛙竟活活地给煮死了.阅读材料陡 峭程 度平均变化率 的绝对值（越大）（越小）（越小）（越大）数学探究作业布置课本:P.34 练习2作业纸: 课本:P.34 练习1完成:学案 P.120-121预习:课本:P.34-38　　　　　　　　　　　　　　　　　　　　——华罗庚天才在于积累。
聪明在于勤奋，临沂一中谢谢大家!