函数的奇偶性公开课

课件21张PPT。第三章 函数 3.2.2 函数的奇偶性一、创设情景
创 设 情 景 兴 趣 导 入
观察这些生活中的图片，你发现了什么？创 设 情 景
兴 趣 导 入
创 设 情 景 兴 趣 导 入
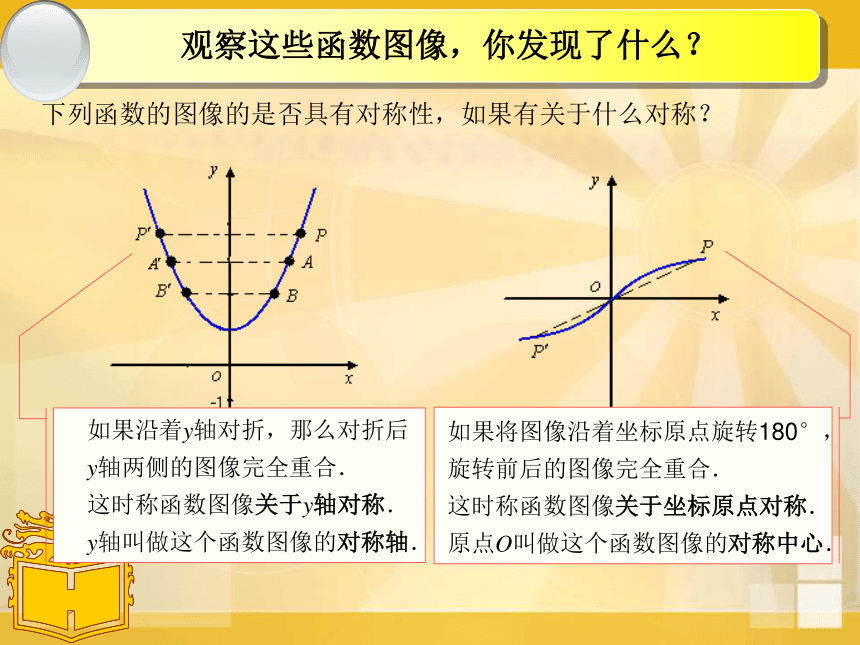
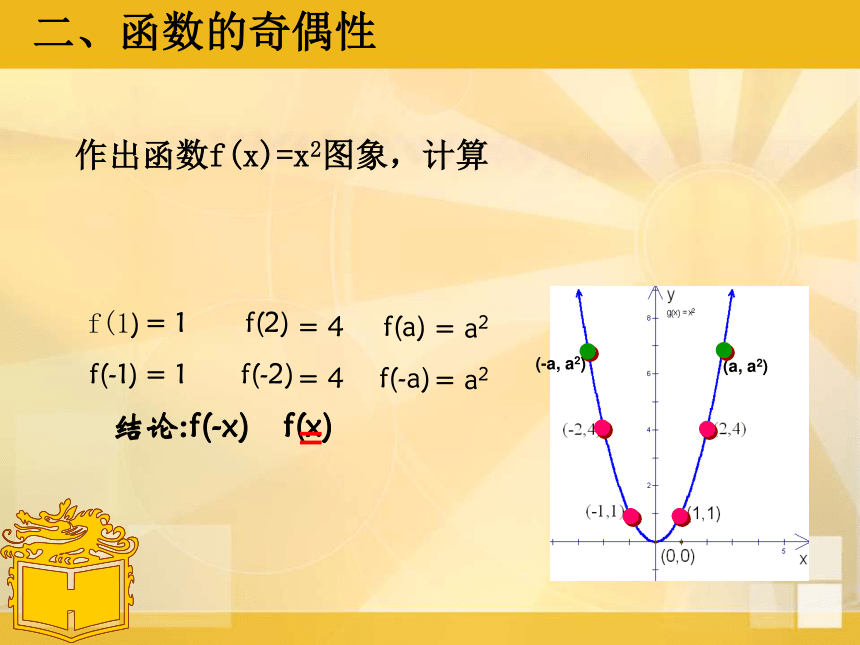
下列函数的图像的是否具有对称性，如果有关于什么对称？ 从图象对称的角度把这些函数图象分类⑥作出函数f(x)=x2图象，计算结论:f(-x) f(x)=二、函数的奇偶性
已知f(x)=x3图象,求出f(-2),f(2),f(-1),f(1)
及f(-a)解:f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)f(-1)=(-1)3=-1, f(1)=1 f(-1)= - f(1)f(-a)=(-a)3=-a3 =-f(a)
(-x,-y)(x,y)结论： f(-x) - f(x)=.对任意的x∈D，都有 ? x ∈ D分析理解定义： （1）偶函数图像关于y轴对称；奇函数图像关于原点对称。 练习1： 通过对图像对称性的观察，判断下面的三个函数是否具有奇偶性．
练习2、我们初中学过的函数中，说出哪些函数具有奇偶性，是奇函数，还是偶函数？正比例函数y=kx; 反比例函数二次函数中的分析理解定义： （2）由f(-x)=f(x) ，即如果函数y=f(x)是偶函数,则当自变量x取一对相反数时，相应的两个函数值相等.
由f(-x)=-f(x),即如果函数y=f(x)是奇函数,则当自变量x取一对相反数时，相应的两个函数值也相反.
例1、1．若函数y＝f(x)是奇函数，且f(-1)=3,则f(1)等于......( )
A．0 B．－1 C．3 D．－3
解析：由题知f(－1)＝3，因为f(x)为奇函数，所以 f(1)＝－3.
答案：D
练习3：1）若函数y＝f(x)是奇函数，且f(5)=-8,则f(-5)=______;
2) 若函数是偶函数，且f(-3)=-3,则f(3)=____;8-3分析理解定义： （3）函数具有奇偶性：。对于定义域内的任意一个x，则－x也一定是定义域内的一个自变量,即定义域必须关于原点对称.
定义域不关于原点对称，是非奇非偶函数例2、 如果定义在区间[2－a,4]上的函数f(x)为偶函数，那么a＝________.
解：因为奇偶函数的前提是定义域必须关于原点对称，
所以2－a＝－4，
∴a＝6.
练习4、1）如果定义在区间[-2,a]上的函数f(x)为偶函数，那么a＝________.
2)如果定义在区间[2a+1,3]上的函数f(x)为奇函数，那么a＝________.2-2..分析　依照判断函数奇偶性的基本步骤进行．图象关于y轴对称f(-x)=f(x)偶函数四、小结图象关于原点对称f(-x)= - f(x)奇函数再 见