人教版八年级下册18.2.3 正方形 课件(共14张PPT)
文档属性
| 名称 | 人教版八年级下册18.2.3 正方形 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 183.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 09:23:15 | ||
图片预览





文档简介
(共14张PPT)
第18章 平行四边形
18.2 特殊的平行四边形
18.2.3 正方形
学
目
习
标
1.掌握正方形的概念、性质,并能灵活运用.
2.理解正方形与平行四边形、矩形、菱形的联系和区别.
3.根据平行四边形、矩形、菱形与正方形之间的关系,归纳出正方形的判定定理.
4.能运用正方形的判定定理进行简单的计算与证明.
5.能运用正方形的性质定理和判定定理进行比较简单的综合推理与证明.
预
反
习
馈
阅读教材P58~59,完成下列问题.
定义及性质:
(1)定义:一组 ,并且有一个角是 的 叫做正方形.
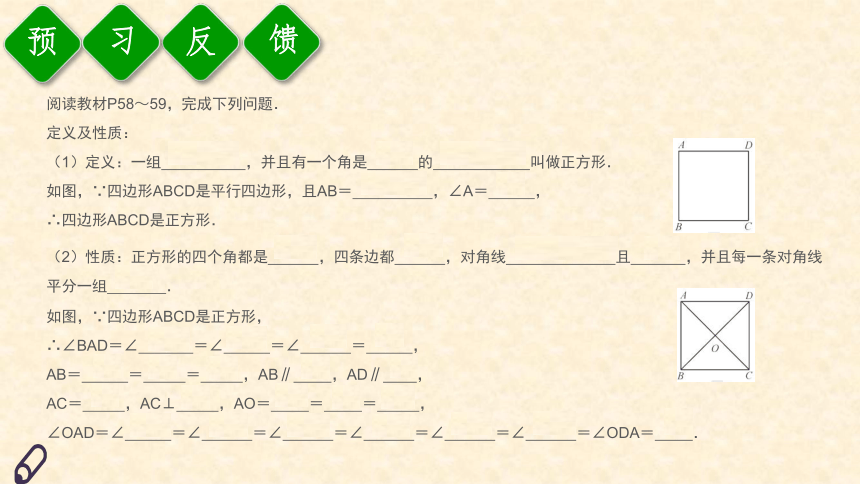
如图,∵四边形ABCD是平行四边形,且AB= ,∠A= ,
∴四边形ABCD是正方形.
(2)性质:正方形的四个角都是 ,四条边都 ,对角线 且 ,并且每一条对角线平分一组 .
如图,∵四边形ABCD是正方形,
∴∠BAD=∠ =∠ =∠ = ,
AB= = = ,AB∥ ,AD∥ ,
AC= ,AC⊥ ,AO= = = ,
∠OAD=∠ =∠ =∠ =∠ =∠ =∠ =∠ODA= .
邻边相等
直角
平行四边形
BC或AD
90°
直角
相等
互相垂直平分
相等
对角
ABC
BCD
CDA
90°
BC
CD
DA
CD
BC
BD
BD
CO
BO
DO
OAB
OBA
OBC
OCB
OCD
ODC
45°
预
反
习
馈
判定:
(1)用定义判定:一组 ,并且有一个角是 的平行四边形是正方形.
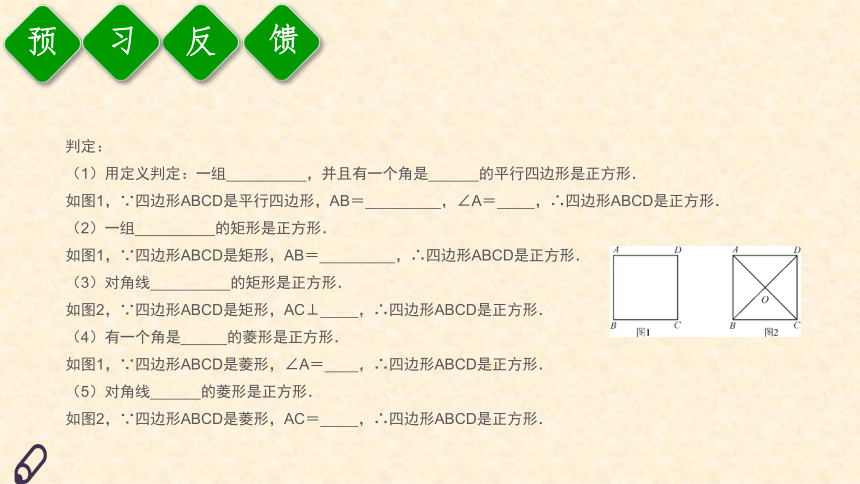
如图1,∵四边形ABCD是平行四边形,AB= ,∠A= ,∴四边形ABCD是正方形.
(2)一组 的矩形是正方形.
如图1,∵四边形ABCD是矩形,AB= ,∴四边形ABCD是正方形.
(3)对角线 的矩形是正方形.
如图2,∵四边形ABCD是矩形,AC⊥ ,∴四边形ABCD是正方形.
(4)有一个角是 的菱形是正方形.
如图1,∵四边形ABCD是菱形,∠A= ,∴四边形ABCD是正方形.
(5)对角线 的菱形是正方形.
如图2,∵四边形ABCD是菱形,AC= ,∴四边形ABCD是正方形.
BC或AD
90°
邻边相等
邻边相等
BC或AD
互相垂直
BD
90°
直角
相等
直角
BD
名
讲
校
坛
例1 (教材P58例5)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知:如图,正方形ABCD对角线AC,BD相交于O点.
求证:△ABO,△BCO,△CDO,△ADO是全等的等腰直角三角形.
【解答】 ∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.
【方法归纳】 对于正方形性质,应注意应用其性质及由性质得到的一些结论:
①四角相等,均为90°,四边相等;②对角线互相垂直平分且相等;
③对角线平分一组对角得到45°角;④边长与对角线的长度比为1∶ .
名
讲
校
坛
【跟踪训练1】 (12.2.3习题)如图,正方形ABCD的对角线AC,
BD相交于点O,OA=3,则此正方形的面积为( C )
A.3 B.12 C.18 D.36
【跟踪训练2】 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.求证:AP=BQ.
证明:∵四边形ABCD是正方形,∴AB=AD,∠DAB=90°.∴∠BAQ+∠DAP=90°.
∵DP⊥AQ,∴∠APD=90°.∴∠ADP+∠DAP=90°.∴∠ADP=∠BAQ.
∵AQ⊥BE,∴∠BQA=90°.
在△DAP和△ABQ中, ,
∴△DAP≌△ABQ(AAS).∴AP=BQ.
名
讲
校
坛
例2 (教材补充例题)如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
【解答】 (1)证明:∵AF∥BC,∴∠EAF=∠EDB.∵E是AD的中点,∴AE=DE.
在△AEF和△DEB中, ,∴△AEF≌△DEB(ASA).∴AF=BD.
∵在△ABC中,∠BAC=90°,AD是中线,∴AD=BD=DC= BC.∴AD=AF.
(2)四边形ADCF是正方形.
证明:∵AF=BD=DC,AF∥BC,∴四边形ADCF是平行四边形.
∵AB=AC,AD是中线,∴AD⊥BC.∵AD=AF,∴四边形ADCF是正方形.
名
讲
校
坛
【跟踪训练3】 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= 时,四边形BFDE是正方形.
证明:∵在菱形ABCD中,BA=BC,
∴∠BAC=∠BCA.∴∠BAE=∠BCF.
在△BAE和△BCF中,
∴△BAE≌△BCF(SAS).
20°
巩
训
固
练
1.正方形具有而菱形不一定具有的性质是( B )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.对角相等
2.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等
腰三角形有( C )
A.4个 B.6个
C.8个 D.10个
3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:
①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补
充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中
错误的是( B )
A.①② B.②③ C.①③ D.②④
巩
训
固
练
4.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( B )
A.30 B.34 C.36 D.40
5.如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,OE⊥CD,则OE= .
6.如图,在正方形ABCD内取一点E,使△EBC是等边三角形,∠AED等于 度.
2
150
巩
训
固
练
7.在正方形ABCD中,AC为对角线,E为AC上一点,连接EB,ED.求证:∠BEC=∠DEC.
证明:∵四边形ABCD是正方形,∴CD=CB,∠DCA=∠BCA.
在△BEC与△DEC中, ,
∴△BEC≌△DEC(SAS).∴∠BEC=∠DEC.
巩
训
固
练
8.如图,已知在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,CE=CF.
(1)求证:△BEC≌△DFC;
(2)若DF=5,CE=3,求正方形ABCD的面积.
解:(1)证明:在△BCE和△DCF中, ,
∴△BEC≌△DFC(SAS).
(2)由题知,CF=CE=3.
在Rt△DCF中,CD= =4.
∴正方形的面积为4×4=16.
课
小
堂
结
THANK YOU!
第18章 平行四边形
18.2 特殊的平行四边形
18.2.3 正方形
学
目
习
标
1.掌握正方形的概念、性质,并能灵活运用.
2.理解正方形与平行四边形、矩形、菱形的联系和区别.
3.根据平行四边形、矩形、菱形与正方形之间的关系,归纳出正方形的判定定理.
4.能运用正方形的判定定理进行简单的计算与证明.
5.能运用正方形的性质定理和判定定理进行比较简单的综合推理与证明.
预
反
习
馈
阅读教材P58~59,完成下列问题.
定义及性质:
(1)定义:一组 ,并且有一个角是 的 叫做正方形.
如图,∵四边形ABCD是平行四边形,且AB= ,∠A= ,
∴四边形ABCD是正方形.
(2)性质:正方形的四个角都是 ,四条边都 ,对角线 且 ,并且每一条对角线平分一组 .
如图,∵四边形ABCD是正方形,
∴∠BAD=∠ =∠ =∠ = ,
AB= = = ,AB∥ ,AD∥ ,
AC= ,AC⊥ ,AO= = = ,
∠OAD=∠ =∠ =∠ =∠ =∠ =∠ =∠ODA= .
邻边相等
直角
平行四边形
BC或AD
90°
直角
相等
互相垂直平分
相等
对角
ABC
BCD
CDA
90°
BC
CD
DA
CD
BC
BD
BD
CO
BO
DO
OAB
OBA
OBC
OCB
OCD
ODC
45°
预
反
习
馈
判定:
(1)用定义判定:一组 ,并且有一个角是 的平行四边形是正方形.
如图1,∵四边形ABCD是平行四边形,AB= ,∠A= ,∴四边形ABCD是正方形.
(2)一组 的矩形是正方形.
如图1,∵四边形ABCD是矩形,AB= ,∴四边形ABCD是正方形.
(3)对角线 的矩形是正方形.
如图2,∵四边形ABCD是矩形,AC⊥ ,∴四边形ABCD是正方形.
(4)有一个角是 的菱形是正方形.
如图1,∵四边形ABCD是菱形,∠A= ,∴四边形ABCD是正方形.
(5)对角线 的菱形是正方形.
如图2,∵四边形ABCD是菱形,AC= ,∴四边形ABCD是正方形.
BC或AD
90°
邻边相等
邻边相等
BC或AD
互相垂直
BD
90°
直角
相等
直角
BD
名
讲
校
坛
例1 (教材P58例5)求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.
已知:如图,正方形ABCD对角线AC,BD相交于O点.
求证:△ABO,△BCO,△CDO,△ADO是全等的等腰直角三角形.
【解答】 ∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴△ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.
【方法归纳】 对于正方形性质,应注意应用其性质及由性质得到的一些结论:
①四角相等,均为90°,四边相等;②对角线互相垂直平分且相等;
③对角线平分一组对角得到45°角;④边长与对角线的长度比为1∶ .
名
讲
校
坛
【跟踪训练1】 (12.2.3习题)如图,正方形ABCD的对角线AC,
BD相交于点O,OA=3,则此正方形的面积为( C )
A.3 B.12 C.18 D.36
【跟踪训练2】 如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.求证:AP=BQ.
证明:∵四边形ABCD是正方形,∴AB=AD,∠DAB=90°.∴∠BAQ+∠DAP=90°.
∵DP⊥AQ,∴∠APD=90°.∴∠ADP+∠DAP=90°.∴∠ADP=∠BAQ.
∵AQ⊥BE,∴∠BQA=90°.
在△DAP和△ABQ中, ,
∴△DAP≌△ABQ(AAS).∴AP=BQ.
名
讲
校
坛
例2 (教材补充例题)如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
【解答】 (1)证明:∵AF∥BC,∴∠EAF=∠EDB.∵E是AD的中点,∴AE=DE.
在△AEF和△DEB中, ,∴△AEF≌△DEB(ASA).∴AF=BD.
∵在△ABC中,∠BAC=90°,AD是中线,∴AD=BD=DC= BC.∴AD=AF.
(2)四边形ADCF是正方形.
证明:∵AF=BD=DC,AF∥BC,∴四边形ADCF是平行四边形.
∵AB=AC,AD是中线,∴AD⊥BC.∵AD=AF,∴四边形ADCF是正方形.
名
讲
校
坛
【跟踪训练3】 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= 时,四边形BFDE是正方形.
证明:∵在菱形ABCD中,BA=BC,
∴∠BAC=∠BCA.∴∠BAE=∠BCF.
在△BAE和△BCF中,
∴△BAE≌△BCF(SAS).
20°
巩
训
固
练
1.正方形具有而菱形不一定具有的性质是( B )
A.对角线互相垂直 B.对角线相等
C.对角线互相平分 D.对角相等
2.如图,在正方形ABCD中,对角线AC,BD相交于点O,则图中的等
腰三角形有( C )
A.4个 B.6个
C.8个 D.10个
3.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:
①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补
充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中
错误的是( B )
A.①② B.②③ C.①③ D.②④
巩
训
固
练
4.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( B )
A.30 B.34 C.36 D.40
5.如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,OE⊥CD,则OE= .
6.如图,在正方形ABCD内取一点E,使△EBC是等边三角形,∠AED等于 度.
2
150
巩
训
固
练
7.在正方形ABCD中,AC为对角线,E为AC上一点,连接EB,ED.求证:∠BEC=∠DEC.
证明:∵四边形ABCD是正方形,∴CD=CB,∠DCA=∠BCA.
在△BEC与△DEC中, ,
∴△BEC≌△DEC(SAS).∴∠BEC=∠DEC.
巩
训
固
练
8.如图,已知在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,CE=CF.
(1)求证:△BEC≌△DFC;
(2)若DF=5,CE=3,求正方形ABCD的面积.
解:(1)证明:在△BCE和△DCF中, ,
∴△BEC≌△DFC(SAS).
(2)由题知,CF=CE=3.
在Rt△DCF中,CD= =4.
∴正方形的面积为4×4=16.
课
小
堂
结
THANK YOU!
