万有引力与宇宙航行章节小练 (word版含答案)
文档属性
| 名称 | 万有引力与宇宙航行章节小练 (word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 524.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-11 22:47:55 | ||
图片预览




文档简介
万有引力与宇宙航行
一、单选题
1.下列说法中正确的是( )
A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力
B.根据表达式可知,当r趋近于零时,万有引力趋近于无穷大
C.牛顿发现了万有引力定律,并测出了引力常量G
D.开普勒第三定律得出的表达式,其中k是一个与中心天体无关的常量
2.两颗人造卫星A、B绕地球做圆周运动,周期之比为,则轨道半径之比和运动速率之比分别为( )
A., B.,
C., D.,
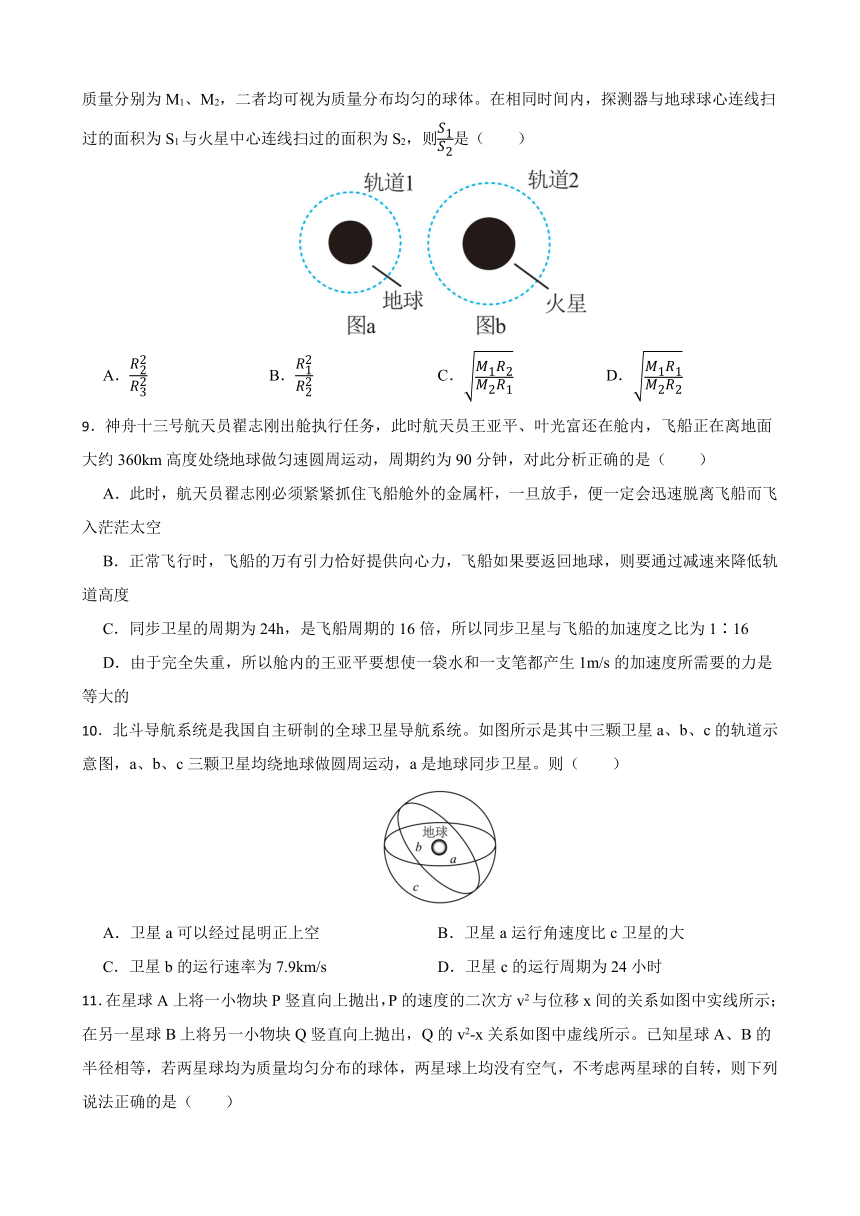
3.有一卫星绕地球沿椭圆轨道运行。卫星从近地点向远地点运动过程中,受地球引力的大小变化情况是( )
A.不变 B.一直减小
C.一直增大 D.先增大后减小
4.中国探月工程又称嫦娥工程,实现月球探测将是我国航天深空探测突破的开端。在地球和月球的连线上有一个非常特殊的点,物体(大小可以忽略)在该点时,地球和月球对该物体的万有引力大小相等、方向相反。已知地球质量约为月球质量的81倍,地球半径约为月球半径的4倍,则该点距离地球中心和月球中心的距离之比为( )
A.9:1 B.18:1 C.1∶2 D.324:1
5.某星球可视为质量均匀分布的球体,已知该星球表面的重力加速度在两极的大小为 ,在赤道的大小为 ,星球自转周期为T,则该星球的半径R为( )
A. B.
C. D.
6.牛顿在发现万有引力定律后曾思考过这样一个问题:假设地球是一个质量均匀分布的球体,已知质量分布均匀的球壳对球壳内物体的引力为零.沿地球的南北极打一个内壁光滑的洞,在洞的上端无初速释放一个小球(小球的直径略小于洞的直径),在小球向下端运动的过程中,你可能不会推导小球速度随时间变化的表示式,但是你可以用所学过的物理知识定性画出小球的速度与时间图象,取向下为正方向,则下列图象中正确的是( )
A. B.
C. D.
7.2021年6月17日,神舟十二号载人飞船与长征二号F遥十二运载火箭组合体搭载航天员聂海胜、刘伯明、汤洪波先后进入“天和核心舱”,中国人首次进入自己的空间站。已知空间站在离地面约为 的圆轨道做匀速圆周运动,则下列说法正确的是( )
A.空间站在轨运行周期约为
B.空间站在轨运行速度一定小于
C.发射运载火箭的速度需要超过第二宇宙速度才能完成对接
D.航天员乘坐的载人飞船需先进入空间站轨道,再加速追上空间站完成对接
8.2021年5月15日,中国首次火星探测任务“天问一号”着陆巡视器安全“到站”,着陆乌托邦平原,红色火星第一次留下了中国印迹。在发射探测器的过程中,探测器绕地球在轨道1上做匀速圆周运动的轨道半径为R1(图a),绕火星在轨道2上做匀速圆周运动的轨道半径为R2(图b)。地球与火星的质量分别为M1、M2,二者均可视为质量分布均匀的球体。在相同时间内,探测器与地球球心连线扫过的面积为S1与火星中心连线扫过的面积为S2,则是( )
A. B. C. D.
9.神舟十三号航天员翟志刚出舱执行任务,此时航天员王亚平、叶光富还在舱内,飞船正在离地面大约360km高度处绕地球做匀速圆周运动,周期约为90分钟,对此分析正确的是( )
A.此时,航天员翟志刚必须紧紧抓住飞船舱外的金属杆,一旦放手,便一定会迅速脱离飞船而飞入茫茫太空
B.正常飞行时,飞船的万有引力恰好提供向心力,飞船如果要返回地球,则要通过减速来降低轨道高度
C.同步卫星的周期为24h,是飞船周期的16倍,所以同步卫星与飞船的加速度之比为1∶16
D.由于完全失重,所以舱内的王亚平要想使一袋水和一支笔都产生1m/s的加速度所需要的力是等大的
10.北斗导航系统是我国自主研制的全球卫星导航系统。如图所示是其中三颗卫星a、b、c的轨道示意图,a、b、c三颗卫星均绕地球做圆周运动,a是地球同步卫星。则( )
A.卫星a可以经过昆明正上空 B.卫星a运行角速度比c卫星的大
C.卫星b的运行速率为7.9km/s D.卫星c的运行周期为24小时
11.在星球A上将一小物块P竖直向上抛出,P的速度的二次方v2与位移x间的关系如图中实线所示;在另一星球B上将另一小物块Q竖直向上抛出,Q的v2-x关系如图中虚线所示。已知星球A、B的半径相等,若两星球均为质量均匀分布的球体,两星球上均没有空气,不考虑两星球的自转,则下列说法正确的是( )
A.星球A表面的重力加速度是星球B表面的重力加速度的
B.A的密度是B的密度的3倍
C.P抛出后落回原处的时间是Q抛出后落回原处的时间的
D.A的第一宇宙速度是B的第一宇宙速度的倍
12.如图所示,虚线I、II、III分别表示地球卫星的三条轨道,其中轨道I为与第一宇宙速度7.9km/s对应的近地环绕圆轨道,轨道II为椭圆轨道,轨道III为与第二宇宙速度11.2km/s对应的脱离轨道,a、b、c三点分别位于三条轨道上,b点为轨道II的远地点,b、c点与地心的距离均为轨道I半径的2倍,则( )
A.卫星在轨道II的运行周期为轨道I周期的2倍
B.卫星经过a点的速率为经过b点速率的倍
C.卫星在a点的加速度大小为在c点加速度大小的2倍
D.质量相同的卫星在b点的机械能小于在c点的机械能
13.一宇航员到达半径为R、密度均匀的某星球表面,做了如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定于O点,如图甲所示。在最低点给小球一初速度,使其绕O点在竖直面内做圆周运动,测得轻绳拉力F的大小随时间t的变化规律如图乙所示,,设R、m、引力常量G和均为已知量,忽略各种阻力。下列说法正确的是( )
A.该星球表面的重力加速度为
B.该星球的密度为
C.该星球的第一宇宙速度为
D.卫星绕该星球运行的最小周期为
14.我国首个火星探测器“天问一号”在2021年5月15日成功着陆于火星表面,开始对火星进行探测。已知火星的质量约为地球质量的十分之一,半径约为地球半径的二分之一,自转周期大约为24小时37分钟,则火星的同步卫星与地球同步卫星轨道半径之比约为( )
A.2 B.3 C.0.5 D.0.3
15.宇宙用有一孤立星系,中心天体对周围有三颗行星,如图所示,中心天体质量大于行星质量,不考虑行星之间的万有引力,行星Ⅰ、Ⅲ为圆轨道,半径分别为,,行星Ⅱ为椭圆轨道,半长轴为a,,与行星Ⅰ轨道在B点相切,下列说法正确的是( )
A.行星Ⅱ与行星Ⅲ的运行周期相等
B.行星Ⅱ在P点与行星Ⅲ在D点时的加速度相同
C.行星Ⅲ的速率大于行星Ⅱ在B点的速率
D.行星Ⅰ的速率与行星Ⅱ在B点的速率相等
二、填空题
16.已知地球半径R=6.37×103km,假设地球是一个标准的圆球体,位于北纬30°附近的某地有一质点A,其随地球自转的线速度为 m/s,A的向心加速度方向沿 方向(选填AO、AB、AC)。
17.天文学家发现冥王星的小卫星,其中卫星1绕冥王星运行轨道半径r1 = 19600 km,周期T1 = 6.34天。卫星2绕冥王星运行轨道半径r2 = 48000 km,则其周期T2约为 天,其线速度 卫星1的线速度(选填“大于”、“等于”或“小于”)。
18.圆周运动的一些知识将是接下来学习万有引力与宇宙航行的基础。请回答以下问题:
(1)人骑着自行车在水平面内做半径为R的匀速圆周运动,由于圆周运动的R较大,人和车都可以视为质点,自行车的线速度为v,则自行车的向心加速度可表示为 ,若人的质量为 ,则人所需的向心力大小为 。
(2)月球绕地球的运动可以近似看作匀速圆周运动,轨道半径为r,周期为T,则月球中心的向心加速度可表示为 ,月球的质量为 ,则月球做圆周运动的向心力为 。
19.如图,假设地球质量分布均匀,距地心O为r处的B点,有一质量为m的质点。已知地球质量为M,引力常量为G,类比电场强度的定义式,可推知地球在B点的引力场强度大小为 ;类比磁场中的磁通量,若要在电场中引入电通量 的概念,你认为可用 表示,并对你的表达式中的物理量符号进行说明: 。
20.两行星A和B是两个均匀球体,行星A的卫星a沿圆轨道运行的周期为 ;行星B的卫星b沿圆轨道运行的周期为 。设两卫星均为各自中心星体的近地卫星,而且 ,行星A和行星B的半径之比为 ,两行星的质量之比MA:MB = ,则行星A和行星B的密度之比 = ,行星表面的重力加速度之比 = 。
三、计算题
21.已知地球的质量为6.0x1024kg,太阳的质量为2.0x1030kg ,它们之间的距离为1.5x1011m. 试计算地球和太阳之间的万有引力的大小?(数量级正确即可,G=6.67x10-11Nm2/kg2)
22.两颗靠的较近的天体称为双星,它们以两者的连线上某点为圆心做匀速圆周运动,而不会由于万有引力作用,使它们吸在一起(不考虑其他天体对它们的影响),已知两天体质量分别为m1和m2,相距为L,求它们运转的角速度 。
23.月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天,应用开普勒定律计算:在赤道平面内离地多高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样?(R地=6400km)
答案部分
1.A 2.C 3.B 4.A 5.A
6.B 7.B 8.D 9.B 10.D
11.B 12.D 13.D 14.C 15.A
16.400.9;AB
17.24.3;小于
18.(1);
(2);
19.;;电场强度类比为磁感应强度,则可得电通量为 表达式中E表示电场强度,S表示面积,θ表示面积与电场垂直方向投影面积的夹角。
20.2∶1;16∶1;8∶1
21.由太阳对行星的吸引力满足F= 知:F=3.56X1022N.
22.他们之间的相互作用力充当向心力,所以有:
r1+r2=L
联立三式可得
23.月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天;同步卫星的周围为1天;根据开普勒第三定律,有:解得:R月= R同= R同=9R同由于R月=60R地,故R同= R地,故:h= R地= x6400KM=36267km.答:在赤道平面内离地36267km高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样.
解析部分
1.A
【解析】A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力,A符合题意;
B.根据表达式
可知,当r趋近于零时,万有引力定律不再适用,B不符合题意;
C.牛顿发现了万有引力定律,卡文迪许测出了引力常量G,C不符合题意;
D.开普勒第三定律得出的表达式
其中k是一个与中心天体有关的常量,D不符合题意。
2.C
【解析】根据开普勒第三定律可知
解得
根据
解得
3.B
【解析】根据万有引力定律可知,卫星从近地点向远地点运动过程中,卫星与地球之间的距离逐渐变大,可知卫星受地球引力一直减小。
4.A
【解析】设该点到地心的距离为r1,到月心的距离为r2,由万有引力定律可得
整理得
A符合题意。
5.A
【解析】在两极
在赤道
联立可解
6.B
【解析】由题意可知,小球在光滑的洞中运动时,所受万有引力的合力先变小后变大,速度先增大后减小,在地心处时速度最大,加速度为零。
7.B
【解析】A.由
得
由于空间站轨道半径小于同步地球卫星轨道半径,则运行周期小于 ,则A不符合题意;
B.第一宇宙速度是地球卫星的最大运行速度,故空间站在轨运行速度不可能大于 ,则B符合题意;
C.地球卫星发射速度在第一宇宙速度到第二宇宙速度之间,则C不符合题意;
D.完成对接。应先进入较小轨道,再在适当位置加速变轨完成对接,则D不符合题意。
8.D
【解析】由几何关系可知,扫过的面积与扫过的面积成正比,设探测器与地球球心连线在
时间扫过的圆心角为
,则有
由
可得
同理可得
探测器绕地球做匀速圆周运动有
解得
联立可得
同理可得
则
9.B
【解析】A.航天员也相当于一颗卫星,轻轻放手,航天员会和卫星一起相伴做圆周运动,A不符合题意;
B.正常飞行时,飞船的万有引力恰好提供向心力,飞船如果要返回地球,则要通过减速来降低轨道高度,B符合题意;
C.设神州十三号飞船的周期为T1,轨道半径为r1,同步卫星周期为T2,轨道半径为r2。由题意
由开普勒第三定律
又因为向心加速度为
故
故加速度之比不等于1∶16。C不符合题意;
D.由于一袋水和一支笔的质量不一样,产生1m/s的加速度所需要的力是不等大的,D不符合题意。
10.D
【解析】A.卫星a是同步卫星,只能定点在赤道的上空,不可以经过昆明正上空,A不符合题意;
B.根据
可知
由图可知,卫星a与卫星b的半径相等,故卫星a运行角速度与c卫星的角速度相等,B不符合题意;
C.根据
可知,卫星b的轨道半径大于地球的半径,则卫星b的运行速率小于7.9km/s,C不符合题意;
D.卫星ac的轨道半径相同,则两卫星的周期相同,即卫星c的运行周期为24小时,D符合题意。
11.B
【解析】A.根据
可知图像斜率代表重力加速度大小,A、B两星球表面重力加速度之比3:1,A不符合题意;
B.由公式
解得
得A、B星球密度之比为3:1,即A的密度是B的密度的3倍,B符合题意;
C.由图像得P、Q竖直上抛初速度之比
,A、B两星球表面重力加速度之比3:1,根据
所以运动时间之比为
,C不符合题意;
D.根据
解得
A、B两星球表面重力加速度之比3:1,A、B星球第一宇宙速度之比为
,所以A的第一宇宙速度是B的第一宇宙速度的
倍 ,D不符合题意。
12.D
【解析】A.由题可知轨道I的半径与轨道Ⅱ的半长轴之比为
根据开普勒第三定律
解得
A不符合题意;
B.根据
如果b点在过该点的圆形轨道上绕地球做匀速圆周运动,如图所示
卫星经过a点的速率为经过b点的
倍,而轨道Ⅱ是椭圆,因此在轨道Ⅱ上b点的速度不等于圆轨道的速度,B不符合题意;
C.根据公式
可知,卫星在a点的加速度大小为在c点的4倍,C不符合题意;
D.卫星从轨道Ⅱ变到轨道Ⅲ需要点火加速,因此再同一点加速动能增大也就是机械能增大,而同一轨道机械能守恒,因此b点的机械能小于在c点的机械能,D符合题意。
13.D
【解析】A.设砝码在最低点时细线的拉力为
,速度为
,设绳长为L,则
设砝码在最高点细线的拉力为
,速度为
,则
由机械能守恒定律得
解得
因为
所以该星球表面的重力加速度为
A不符合题意;
BC.根据万有引力提供向心力得
卫星绕该星球的第一宇宙速度为
在星球表面,万有引力近似等于重力
解得
星球的密度
卫星绕该星球的第一宇宙速度为
BC不符合题意;
D.卫星绕该星球运行的最小周期,则
解得
D符合题意。
14.C
【解析】由题意可知,火星自转周期约为24小时37分钟,与地球自转周期近似相等,故设火星与地球自转周期为T,根据万有引力提供向心力,可得
解得
故
联立可得
。
15.A
【解析】A.因为行星Ⅱ的运行半径与行星Ⅲ的运行半长轴
则由开普勒第三定律知
则
行星Ⅱ与行星Ⅲ的运行周期相等,A符合题意;
B.由题意知
由
知行星Ⅱ在P点与行星Ⅲ在D点时的加速度大小相等,但方向不同,B不符合题意;
CD.由
得
所以行星Ⅲ的速率小于行星Ⅰ的速率,又因为行星Ⅱ在B点加速才能到达轨道Ⅱ,故行星Ⅱ在B点的速率大于行星Ⅰ在B点的速率,故行星Ⅲ的速率小于行星Ⅱ在B点的速率,CD不符合题意;
16.400.9;AB
【解析】其随地球自转的线速度为
A的向心加速度方向一定指向圆心,不指向地心,沿AB方向。
17.24.3;小于
【解析】 据开普勒第二定律得
周期T2约为24.3天,根据
轨道半径小,线速度大,所以卫星2线速度小于卫星1的线速度。
18.(1);
(2);
【解析】(1)根据向心加速度公式得
向心力为
(2)根据向心加速度公式得
向心力为
19.;;电场强度类比为磁感应强度,则可得电通量为 表达式中E表示电场强度,S表示面积,θ表示面积与电场垂直方向投影面积的夹角。
【解析】电场强度的定义式为
万有引力类比为电场力,质量类比为电荷量,地球在B点的引力场强度大小为 当面积为S的线圈与电场垂直方向投影面积的夹角为θ时,线圈在磁场垂直方向投影面积为Scosθ,磁通量为
电场强度类比为磁感应强度,则可得电通量为 表达式中E表示电场强度,S表示面积,θ表示面积与电场垂直方向投影面积的夹角。
20.2∶1;16∶1;8∶1
【解析】人造地球卫星的万有引力充当向心力,即 ①
体积为 ②
解得密度为 ③
A和B密度之比为 ∶ =16∶1
由 ④
联立②③④得 ⑤
所以 ∶ =2∶1 ⑥忽略行星自转的影响,根据万有引力等于重力列出等式 ⑦
由①⑦解得 ⑧
所以两行星表面处重力加速度之比为 ⑨
21.由太阳对行星的吸引力满足F= 知:F=3.56X1022N.
【解析】由太阳对行星的吸引力满足F=知:F=3.56X1022N
【分析】牢记万有引力定律
22.他们之间的相互作用力充当向心力,所以有:
r1+r2=L
联立三式可得
【解析】他们之间的相互作用力充当向心力,所以有:
r1+r2=L
联立三式可得
23.月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天;同步卫星的周围为1天;根据开普勒第三定律,有:解得:R月= R同= R同=9R同由于R月=60R地,故R同= R地,故:h= R地= x6400KM=36267km.答:在赤道平面内离地36267km高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样.
【解析】月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天;同步卫星的周围为1天;
根据开普勒第三定律,有:
解得:
R月= R同= R同=9R同
由于R月=60R地,故R同= R地,故:
h=R地= x6400KM=36267km.
答:在赤道平面内离地36267km高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样.
一、单选题
1.下列说法中正确的是( )
A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力
B.根据表达式可知,当r趋近于零时,万有引力趋近于无穷大
C.牛顿发现了万有引力定律,并测出了引力常量G
D.开普勒第三定律得出的表达式,其中k是一个与中心天体无关的常量
2.两颗人造卫星A、B绕地球做圆周运动,周期之比为,则轨道半径之比和运动速率之比分别为( )
A., B.,
C., D.,
3.有一卫星绕地球沿椭圆轨道运行。卫星从近地点向远地点运动过程中,受地球引力的大小变化情况是( )
A.不变 B.一直减小
C.一直增大 D.先增大后减小
4.中国探月工程又称嫦娥工程,实现月球探测将是我国航天深空探测突破的开端。在地球和月球的连线上有一个非常特殊的点,物体(大小可以忽略)在该点时,地球和月球对该物体的万有引力大小相等、方向相反。已知地球质量约为月球质量的81倍,地球半径约为月球半径的4倍,则该点距离地球中心和月球中心的距离之比为( )
A.9:1 B.18:1 C.1∶2 D.324:1
5.某星球可视为质量均匀分布的球体,已知该星球表面的重力加速度在两极的大小为 ,在赤道的大小为 ,星球自转周期为T,则该星球的半径R为( )
A. B.
C. D.
6.牛顿在发现万有引力定律后曾思考过这样一个问题:假设地球是一个质量均匀分布的球体,已知质量分布均匀的球壳对球壳内物体的引力为零.沿地球的南北极打一个内壁光滑的洞,在洞的上端无初速释放一个小球(小球的直径略小于洞的直径),在小球向下端运动的过程中,你可能不会推导小球速度随时间变化的表示式,但是你可以用所学过的物理知识定性画出小球的速度与时间图象,取向下为正方向,则下列图象中正确的是( )
A. B.
C. D.
7.2021年6月17日,神舟十二号载人飞船与长征二号F遥十二运载火箭组合体搭载航天员聂海胜、刘伯明、汤洪波先后进入“天和核心舱”,中国人首次进入自己的空间站。已知空间站在离地面约为 的圆轨道做匀速圆周运动,则下列说法正确的是( )
A.空间站在轨运行周期约为
B.空间站在轨运行速度一定小于
C.发射运载火箭的速度需要超过第二宇宙速度才能完成对接
D.航天员乘坐的载人飞船需先进入空间站轨道,再加速追上空间站完成对接
8.2021年5月15日,中国首次火星探测任务“天问一号”着陆巡视器安全“到站”,着陆乌托邦平原,红色火星第一次留下了中国印迹。在发射探测器的过程中,探测器绕地球在轨道1上做匀速圆周运动的轨道半径为R1(图a),绕火星在轨道2上做匀速圆周运动的轨道半径为R2(图b)。地球与火星的质量分别为M1、M2,二者均可视为质量分布均匀的球体。在相同时间内,探测器与地球球心连线扫过的面积为S1与火星中心连线扫过的面积为S2,则是( )
A. B. C. D.
9.神舟十三号航天员翟志刚出舱执行任务,此时航天员王亚平、叶光富还在舱内,飞船正在离地面大约360km高度处绕地球做匀速圆周运动,周期约为90分钟,对此分析正确的是( )
A.此时,航天员翟志刚必须紧紧抓住飞船舱外的金属杆,一旦放手,便一定会迅速脱离飞船而飞入茫茫太空
B.正常飞行时,飞船的万有引力恰好提供向心力,飞船如果要返回地球,则要通过减速来降低轨道高度
C.同步卫星的周期为24h,是飞船周期的16倍,所以同步卫星与飞船的加速度之比为1∶16
D.由于完全失重,所以舱内的王亚平要想使一袋水和一支笔都产生1m/s的加速度所需要的力是等大的
10.北斗导航系统是我国自主研制的全球卫星导航系统。如图所示是其中三颗卫星a、b、c的轨道示意图,a、b、c三颗卫星均绕地球做圆周运动,a是地球同步卫星。则( )
A.卫星a可以经过昆明正上空 B.卫星a运行角速度比c卫星的大
C.卫星b的运行速率为7.9km/s D.卫星c的运行周期为24小时
11.在星球A上将一小物块P竖直向上抛出,P的速度的二次方v2与位移x间的关系如图中实线所示;在另一星球B上将另一小物块Q竖直向上抛出,Q的v2-x关系如图中虚线所示。已知星球A、B的半径相等,若两星球均为质量均匀分布的球体,两星球上均没有空气,不考虑两星球的自转,则下列说法正确的是( )
A.星球A表面的重力加速度是星球B表面的重力加速度的
B.A的密度是B的密度的3倍
C.P抛出后落回原处的时间是Q抛出后落回原处的时间的
D.A的第一宇宙速度是B的第一宇宙速度的倍
12.如图所示,虚线I、II、III分别表示地球卫星的三条轨道,其中轨道I为与第一宇宙速度7.9km/s对应的近地环绕圆轨道,轨道II为椭圆轨道,轨道III为与第二宇宙速度11.2km/s对应的脱离轨道,a、b、c三点分别位于三条轨道上,b点为轨道II的远地点,b、c点与地心的距离均为轨道I半径的2倍,则( )
A.卫星在轨道II的运行周期为轨道I周期的2倍
B.卫星经过a点的速率为经过b点速率的倍
C.卫星在a点的加速度大小为在c点加速度大小的2倍
D.质量相同的卫星在b点的机械能小于在c点的机械能
13.一宇航员到达半径为R、密度均匀的某星球表面,做了如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定于O点,如图甲所示。在最低点给小球一初速度,使其绕O点在竖直面内做圆周运动,测得轻绳拉力F的大小随时间t的变化规律如图乙所示,,设R、m、引力常量G和均为已知量,忽略各种阻力。下列说法正确的是( )
A.该星球表面的重力加速度为
B.该星球的密度为
C.该星球的第一宇宙速度为
D.卫星绕该星球运行的最小周期为
14.我国首个火星探测器“天问一号”在2021年5月15日成功着陆于火星表面,开始对火星进行探测。已知火星的质量约为地球质量的十分之一,半径约为地球半径的二分之一,自转周期大约为24小时37分钟,则火星的同步卫星与地球同步卫星轨道半径之比约为( )
A.2 B.3 C.0.5 D.0.3
15.宇宙用有一孤立星系,中心天体对周围有三颗行星,如图所示,中心天体质量大于行星质量,不考虑行星之间的万有引力,行星Ⅰ、Ⅲ为圆轨道,半径分别为,,行星Ⅱ为椭圆轨道,半长轴为a,,与行星Ⅰ轨道在B点相切,下列说法正确的是( )
A.行星Ⅱ与行星Ⅲ的运行周期相等
B.行星Ⅱ在P点与行星Ⅲ在D点时的加速度相同
C.行星Ⅲ的速率大于行星Ⅱ在B点的速率
D.行星Ⅰ的速率与行星Ⅱ在B点的速率相等
二、填空题
16.已知地球半径R=6.37×103km,假设地球是一个标准的圆球体,位于北纬30°附近的某地有一质点A,其随地球自转的线速度为 m/s,A的向心加速度方向沿 方向(选填AO、AB、AC)。
17.天文学家发现冥王星的小卫星,其中卫星1绕冥王星运行轨道半径r1 = 19600 km,周期T1 = 6.34天。卫星2绕冥王星运行轨道半径r2 = 48000 km,则其周期T2约为 天,其线速度 卫星1的线速度(选填“大于”、“等于”或“小于”)。
18.圆周运动的一些知识将是接下来学习万有引力与宇宙航行的基础。请回答以下问题:
(1)人骑着自行车在水平面内做半径为R的匀速圆周运动,由于圆周运动的R较大,人和车都可以视为质点,自行车的线速度为v,则自行车的向心加速度可表示为 ,若人的质量为 ,则人所需的向心力大小为 。
(2)月球绕地球的运动可以近似看作匀速圆周运动,轨道半径为r,周期为T,则月球中心的向心加速度可表示为 ,月球的质量为 ,则月球做圆周运动的向心力为 。
19.如图,假设地球质量分布均匀,距地心O为r处的B点,有一质量为m的质点。已知地球质量为M,引力常量为G,类比电场强度的定义式,可推知地球在B点的引力场强度大小为 ;类比磁场中的磁通量,若要在电场中引入电通量 的概念,你认为可用 表示,并对你的表达式中的物理量符号进行说明: 。
20.两行星A和B是两个均匀球体,行星A的卫星a沿圆轨道运行的周期为 ;行星B的卫星b沿圆轨道运行的周期为 。设两卫星均为各自中心星体的近地卫星,而且 ,行星A和行星B的半径之比为 ,两行星的质量之比MA:MB = ,则行星A和行星B的密度之比 = ,行星表面的重力加速度之比 = 。
三、计算题
21.已知地球的质量为6.0x1024kg,太阳的质量为2.0x1030kg ,它们之间的距离为1.5x1011m. 试计算地球和太阳之间的万有引力的大小?(数量级正确即可,G=6.67x10-11Nm2/kg2)
22.两颗靠的较近的天体称为双星,它们以两者的连线上某点为圆心做匀速圆周运动,而不会由于万有引力作用,使它们吸在一起(不考虑其他天体对它们的影响),已知两天体质量分别为m1和m2,相距为L,求它们运转的角速度 。
23.月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天,应用开普勒定律计算:在赤道平面内离地多高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样?(R地=6400km)
答案部分
1.A 2.C 3.B 4.A 5.A
6.B 7.B 8.D 9.B 10.D
11.B 12.D 13.D 14.C 15.A
16.400.9;AB
17.24.3;小于
18.(1);
(2);
19.;;电场强度类比为磁感应强度,则可得电通量为 表达式中E表示电场强度,S表示面积,θ表示面积与电场垂直方向投影面积的夹角。
20.2∶1;16∶1;8∶1
21.由太阳对行星的吸引力满足F= 知:F=3.56X1022N.
22.他们之间的相互作用力充当向心力,所以有:
r1+r2=L
联立三式可得
23.月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天;同步卫星的周围为1天;根据开普勒第三定律,有:解得:R月= R同= R同=9R同由于R月=60R地,故R同= R地,故:h= R地= x6400KM=36267km.答:在赤道平面内离地36267km高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样.
解析部分
1.A
【解析】A.两物体间的万有引力总是大小相等、方向相反,是一对作用力与反作用力,A符合题意;
B.根据表达式
可知,当r趋近于零时,万有引力定律不再适用,B不符合题意;
C.牛顿发现了万有引力定律,卡文迪许测出了引力常量G,C不符合题意;
D.开普勒第三定律得出的表达式
其中k是一个与中心天体有关的常量,D不符合题意。
2.C
【解析】根据开普勒第三定律可知
解得
根据
解得
3.B
【解析】根据万有引力定律可知,卫星从近地点向远地点运动过程中,卫星与地球之间的距离逐渐变大,可知卫星受地球引力一直减小。
4.A
【解析】设该点到地心的距离为r1,到月心的距离为r2,由万有引力定律可得
整理得
A符合题意。
5.A
【解析】在两极
在赤道
联立可解
6.B
【解析】由题意可知,小球在光滑的洞中运动时,所受万有引力的合力先变小后变大,速度先增大后减小,在地心处时速度最大,加速度为零。
7.B
【解析】A.由
得
由于空间站轨道半径小于同步地球卫星轨道半径,则运行周期小于 ,则A不符合题意;
B.第一宇宙速度是地球卫星的最大运行速度,故空间站在轨运行速度不可能大于 ,则B符合题意;
C.地球卫星发射速度在第一宇宙速度到第二宇宙速度之间,则C不符合题意;
D.完成对接。应先进入较小轨道,再在适当位置加速变轨完成对接,则D不符合题意。
8.D
【解析】由几何关系可知,扫过的面积与扫过的面积成正比,设探测器与地球球心连线在
时间扫过的圆心角为
,则有
由
可得
同理可得
探测器绕地球做匀速圆周运动有
解得
联立可得
同理可得
则
9.B
【解析】A.航天员也相当于一颗卫星,轻轻放手,航天员会和卫星一起相伴做圆周运动,A不符合题意;
B.正常飞行时,飞船的万有引力恰好提供向心力,飞船如果要返回地球,则要通过减速来降低轨道高度,B符合题意;
C.设神州十三号飞船的周期为T1,轨道半径为r1,同步卫星周期为T2,轨道半径为r2。由题意
由开普勒第三定律
又因为向心加速度为
故
故加速度之比不等于1∶16。C不符合题意;
D.由于一袋水和一支笔的质量不一样,产生1m/s的加速度所需要的力是不等大的,D不符合题意。
10.D
【解析】A.卫星a是同步卫星,只能定点在赤道的上空,不可以经过昆明正上空,A不符合题意;
B.根据
可知
由图可知,卫星a与卫星b的半径相等,故卫星a运行角速度与c卫星的角速度相等,B不符合题意;
C.根据
可知,卫星b的轨道半径大于地球的半径,则卫星b的运行速率小于7.9km/s,C不符合题意;
D.卫星ac的轨道半径相同,则两卫星的周期相同,即卫星c的运行周期为24小时,D符合题意。
11.B
【解析】A.根据
可知图像斜率代表重力加速度大小,A、B两星球表面重力加速度之比3:1,A不符合题意;
B.由公式
解得
得A、B星球密度之比为3:1,即A的密度是B的密度的3倍,B符合题意;
C.由图像得P、Q竖直上抛初速度之比
,A、B两星球表面重力加速度之比3:1,根据
所以运动时间之比为
,C不符合题意;
D.根据
解得
A、B两星球表面重力加速度之比3:1,A、B星球第一宇宙速度之比为
,所以A的第一宇宙速度是B的第一宇宙速度的
倍 ,D不符合题意。
12.D
【解析】A.由题可知轨道I的半径与轨道Ⅱ的半长轴之比为
根据开普勒第三定律
解得
A不符合题意;
B.根据
如果b点在过该点的圆形轨道上绕地球做匀速圆周运动,如图所示
卫星经过a点的速率为经过b点的
倍,而轨道Ⅱ是椭圆,因此在轨道Ⅱ上b点的速度不等于圆轨道的速度,B不符合题意;
C.根据公式
可知,卫星在a点的加速度大小为在c点的4倍,C不符合题意;
D.卫星从轨道Ⅱ变到轨道Ⅲ需要点火加速,因此再同一点加速动能增大也就是机械能增大,而同一轨道机械能守恒,因此b点的机械能小于在c点的机械能,D符合题意。
13.D
【解析】A.设砝码在最低点时细线的拉力为
,速度为
,设绳长为L,则
设砝码在最高点细线的拉力为
,速度为
,则
由机械能守恒定律得
解得
因为
所以该星球表面的重力加速度为
A不符合题意;
BC.根据万有引力提供向心力得
卫星绕该星球的第一宇宙速度为
在星球表面,万有引力近似等于重力
解得
星球的密度
卫星绕该星球的第一宇宙速度为
BC不符合题意;
D.卫星绕该星球运行的最小周期,则
解得
D符合题意。
14.C
【解析】由题意可知,火星自转周期约为24小时37分钟,与地球自转周期近似相等,故设火星与地球自转周期为T,根据万有引力提供向心力,可得
解得
故
联立可得
。
15.A
【解析】A.因为行星Ⅱ的运行半径与行星Ⅲ的运行半长轴
则由开普勒第三定律知
则
行星Ⅱ与行星Ⅲ的运行周期相等,A符合题意;
B.由题意知
由
知行星Ⅱ在P点与行星Ⅲ在D点时的加速度大小相等,但方向不同,B不符合题意;
CD.由
得
所以行星Ⅲ的速率小于行星Ⅰ的速率,又因为行星Ⅱ在B点加速才能到达轨道Ⅱ,故行星Ⅱ在B点的速率大于行星Ⅰ在B点的速率,故行星Ⅲ的速率小于行星Ⅱ在B点的速率,CD不符合题意;
16.400.9;AB
【解析】其随地球自转的线速度为
A的向心加速度方向一定指向圆心,不指向地心,沿AB方向。
17.24.3;小于
【解析】 据开普勒第二定律得
周期T2约为24.3天,根据
轨道半径小,线速度大,所以卫星2线速度小于卫星1的线速度。
18.(1);
(2);
【解析】(1)根据向心加速度公式得
向心力为
(2)根据向心加速度公式得
向心力为
19.;;电场强度类比为磁感应强度,则可得电通量为 表达式中E表示电场强度,S表示面积,θ表示面积与电场垂直方向投影面积的夹角。
【解析】电场强度的定义式为
万有引力类比为电场力,质量类比为电荷量,地球在B点的引力场强度大小为 当面积为S的线圈与电场垂直方向投影面积的夹角为θ时,线圈在磁场垂直方向投影面积为Scosθ,磁通量为
电场强度类比为磁感应强度,则可得电通量为 表达式中E表示电场强度,S表示面积,θ表示面积与电场垂直方向投影面积的夹角。
20.2∶1;16∶1;8∶1
【解析】人造地球卫星的万有引力充当向心力,即 ①
体积为 ②
解得密度为 ③
A和B密度之比为 ∶ =16∶1
由 ④
联立②③④得 ⑤
所以 ∶ =2∶1 ⑥忽略行星自转的影响,根据万有引力等于重力列出等式 ⑦
由①⑦解得 ⑧
所以两行星表面处重力加速度之比为 ⑨
21.由太阳对行星的吸引力满足F= 知:F=3.56X1022N.
【解析】由太阳对行星的吸引力满足F=知:F=3.56X1022N
【分析】牢记万有引力定律
22.他们之间的相互作用力充当向心力,所以有:
r1+r2=L
联立三式可得
【解析】他们之间的相互作用力充当向心力,所以有:
r1+r2=L
联立三式可得
23.月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天;同步卫星的周围为1天;根据开普勒第三定律,有:解得:R月= R同= R同=9R同由于R月=60R地,故R同= R地,故:h= R地= x6400KM=36267km.答:在赤道平面内离地36267km高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样.
【解析】月球环绕地球运动的轨道半径为地球半径的60倍,运行周期约为27天;同步卫星的周围为1天;
根据开普勒第三定律,有:
解得:
R月= R同= R同=9R同
由于R月=60R地,故R同= R地,故:
h=R地= x6400KM=36267km.
答:在赤道平面内离地36267km高时,人造地球卫星随地球一起转动,就像停留在天空中不动一样.
