测量课件
图片预览







文档简介
课件20张PPT。§25.1 测量学习目标1,通过探究,明确测量的不同方法。
2,会用相似三角形的相关知识,用不 同的方法解决同一实际问题。
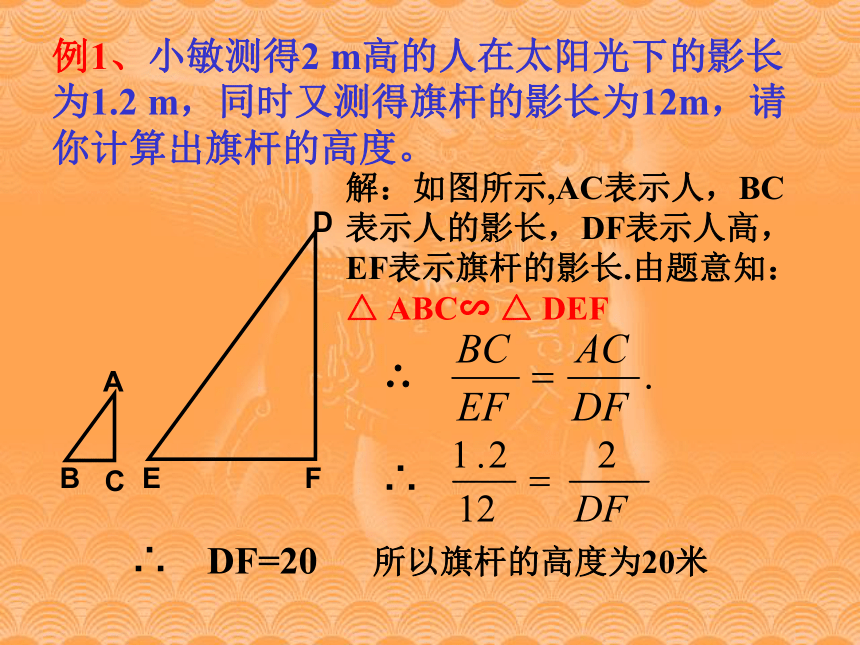
3,明确测量过程中,为了达到目的, 通常将高度分成两部分,使一部分 在直角三角形中,另一部分在四边 形中。实践应用拓展思维 同学们,怎样利用相似三角形的有关知识测量旗杆(或路灯,或树,或烟囱)的高度 ? 利用太阳光求出旗杆的高度。方法1:利用阳光下的影子 为了测量旗杆的高度,除了知道有太阳光线外,还需要测量出哪些值?方法1:利用阳光下的影子 例1、小敏测得2 m高的人在太阳光下的影长为1.2 m,同时又测得旗杆的影长为12m,请你计算出旗杆的高度。解:如图所示,AC表示人,BC表示人的影长,DF表示人高,EF表示旗杆的影长.由题意知:
△ ABC∽ △ DEF∴
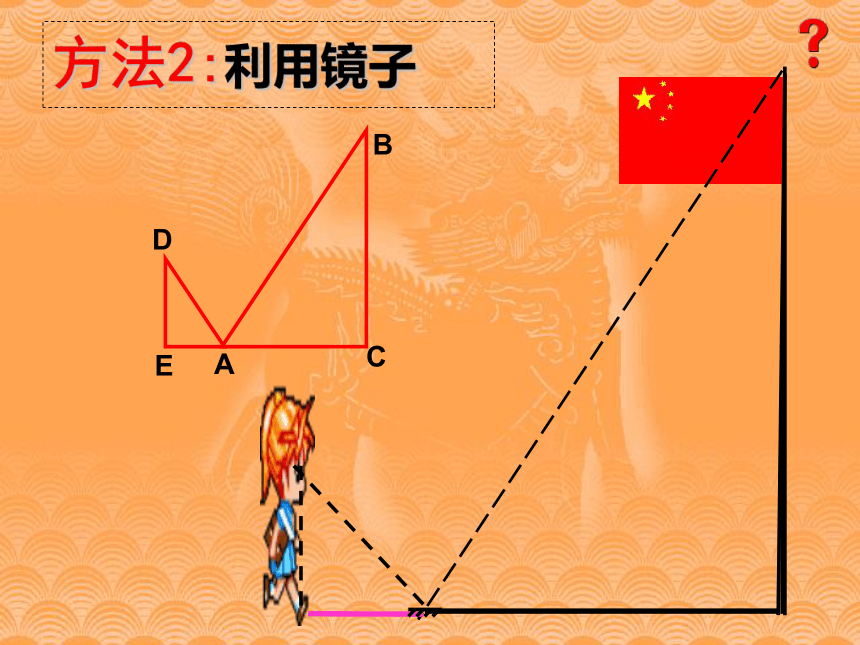
∴ ∴ DF=20所以旗杆的高度为20米 如果是阴天,你还有什么方法可以测量出旗杆的高度呢?思考:方法2:利用镜子例2、如图,在距离旗杆高AB 27米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见旗杆顶。若人眼距地面1.4米,求旗杆高。DBACE 解:由题意知:BE=27米、DE=2.1米、CD=1.4米,且△ ABE∽ △ CDE
∴F答:旗杆高为12米方法3:利用标杆例3.如图,在距离旗杆10米远处放一2米高的标杆,人在离标杆的4米处,此人正好看见标杆的顶端与旗杆的顶端在同一条直线上,此人的眼距地面1.4米,求旗杆的高度?解.由题意知: △ AEF∽ △ABC∴ BC=2.1米 BM=BC+CM=2.1+1.4=3.5米EF=2-1.4=0.6米,AF=DN=4米 MN=CF=10米 AC=AF+FC=10+4=14米答:旗杆的高度是3.5米学习小结 充分利用相似三角形的相关知识在测量中采用不同的方法或者设计不同的方案解决实际问题。34。ABDECA'C'B'方法3也可这样做算一算34。ADECBA'C'B'10米1米旗杆有多高?课外思考 在本节课中,我们利用了相似三角形; 在测量中不用相似三角形的知识,能否利用直角三角形的相关知识来解决呢?请同学们想一想。1. 如图,在距离树AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶。若人眼距地面1.4米,求树高。DBACE当堂训练18米2.1米1.4米 2. 如图,A、B两点分别位于一个池塘的两端,小颖想用绳子测量A、B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A、B点的点C,找到AC、BC的中点D、E,并且DE的长为5m,则A、B两点的距离是多少? 3. 一油桶高0.8m,桶内有油,一根木棒长1米,从桶盖小口斜插入桶内一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.8m,则桶内油面的高度为多少米?4.如图,阳光通过窗口照到室内的地面上2.7m宽的亮区,已知亮区一边到窗下的墙脚距离CE=8.7m,窗口AB=1.8m,那么窗口底边离地面的高BC的长度是多少?再见
2,会用相似三角形的相关知识,用不 同的方法解决同一实际问题。
3,明确测量过程中,为了达到目的, 通常将高度分成两部分,使一部分 在直角三角形中,另一部分在四边 形中。实践应用拓展思维 同学们,怎样利用相似三角形的有关知识测量旗杆(或路灯,或树,或烟囱)的高度 ? 利用太阳光求出旗杆的高度。方法1:利用阳光下的影子 为了测量旗杆的高度,除了知道有太阳光线外,还需要测量出哪些值?方法1:利用阳光下的影子 例1、小敏测得2 m高的人在太阳光下的影长为1.2 m,同时又测得旗杆的影长为12m,请你计算出旗杆的高度。解:如图所示,AC表示人,BC表示人的影长,DF表示人高,EF表示旗杆的影长.由题意知:
△ ABC∽ △ DEF∴
∴ ∴ DF=20所以旗杆的高度为20米 如果是阴天,你还有什么方法可以测量出旗杆的高度呢?思考:方法2:利用镜子例2、如图,在距离旗杆高AB 27米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见旗杆顶。若人眼距地面1.4米,求旗杆高。DBACE 解:由题意知:BE=27米、DE=2.1米、CD=1.4米,且△ ABE∽ △ CDE
∴F答:旗杆高为12米方法3:利用标杆例3.如图,在距离旗杆10米远处放一2米高的标杆,人在离标杆的4米处,此人正好看见标杆的顶端与旗杆的顶端在同一条直线上,此人的眼距地面1.4米,求旗杆的高度?解.由题意知: △ AEF∽ △ABC∴ BC=2.1米 BM=BC+CM=2.1+1.4=3.5米EF=2-1.4=0.6米,AF=DN=4米 MN=CF=10米 AC=AF+FC=10+4=14米答:旗杆的高度是3.5米学习小结 充分利用相似三角形的相关知识在测量中采用不同的方法或者设计不同的方案解决实际问题。34。ABDECA'C'B'方法3也可这样做算一算34。ADECBA'C'B'10米1米旗杆有多高?课外思考 在本节课中,我们利用了相似三角形; 在测量中不用相似三角形的知识,能否利用直角三角形的相关知识来解决呢?请同学们想一想。1. 如图,在距离树AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶。若人眼距地面1.4米,求树高。DBACE当堂训练18米2.1米1.4米 2. 如图,A、B两点分别位于一个池塘的两端,小颖想用绳子测量A、B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A、B点的点C,找到AC、BC的中点D、E,并且DE的长为5m,则A、B两点的距离是多少? 3. 一油桶高0.8m,桶内有油,一根木棒长1米,从桶盖小口斜插入桶内一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.8m,则桶内油面的高度为多少米?4.如图,阳光通过窗口照到室内的地面上2.7m宽的亮区,已知亮区一边到窗下的墙脚距离CE=8.7m,窗口AB=1.8m,那么窗口底边离地面的高BC的长度是多少?再见
