27.2.2相似三角形应用举例
文档属性
| 名称 | 27.2.2相似三角形应用举例 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-15 13:33:42 | ||
图片预览







文档简介
课件24张PPT。乐山大佛新课导入世界上最高的树
—— 红杉世界上最高的楼
——台北101大楼怎样测量这些非常高大物体的高度?世界上最宽的河
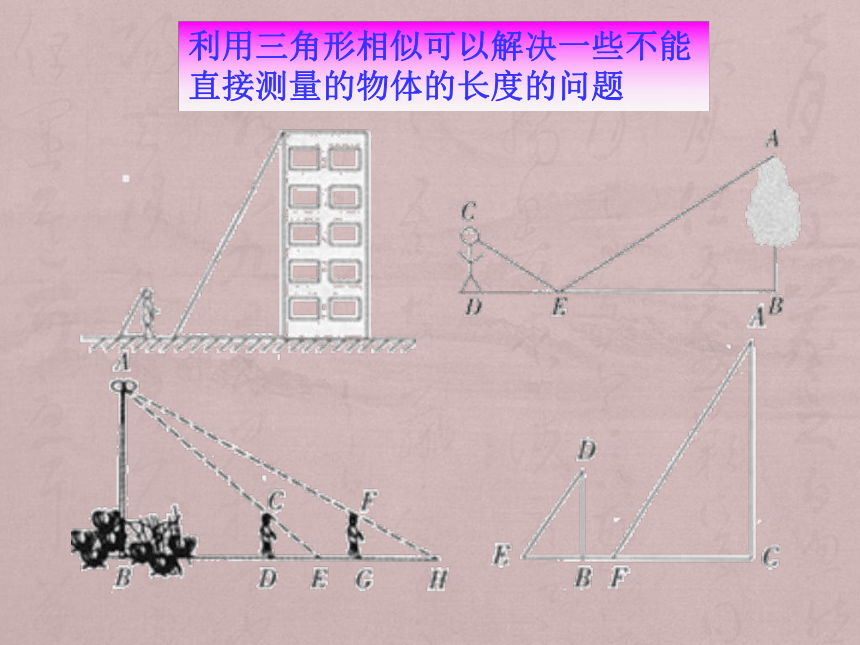
——亚马孙河怎样测量河宽?利用三角形相似可以解决一些不能直接测量的物体的长度的问题 古希腊数学家、天文学家泰勒斯利用相似三角形的原理,测量金字塔的高度。DEA(F)BO2m3m201m解:太阳光是平行线, 因此∠BAO= ∠EDF又 ∠AOB= ∠DFE=90°
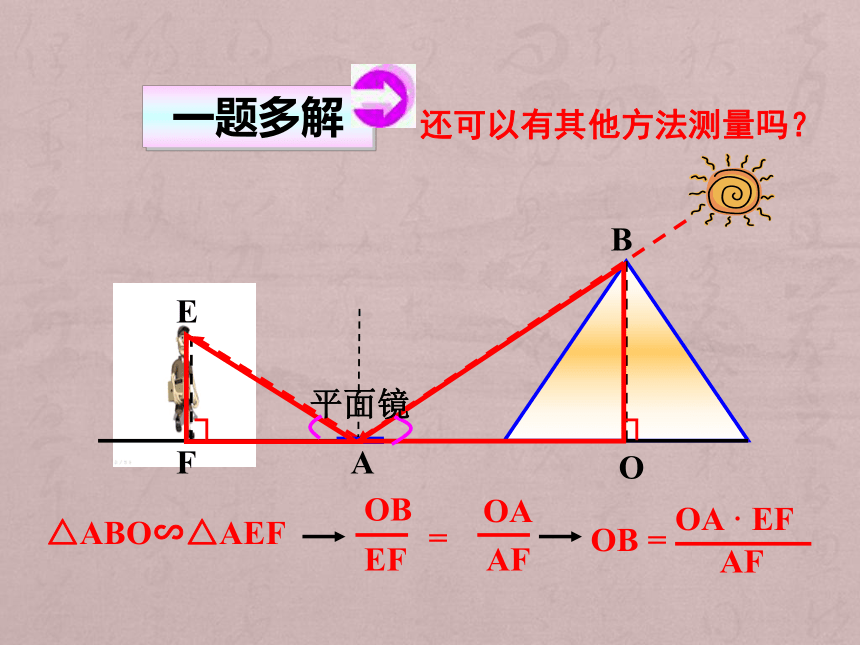
∴△ABO∽△DEF=BO == 134AFEBO┐┐还可以有其他方法测量吗?=△ABO∽△AEFOB =平面镜怎样测量旗杆的高度?6m1.2m1.6m物1高 :物2高 = 影1长 :影2长测高的方法 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。 ∠P=∠P 分析:∵∠PQR=∠PST= 90° STPQRba得 PQ=90求河宽?∴ △PQR ∽△PST∴45m60m90m∴测距的方法 测量不能到达两点间的距离,常构造相似三角形求解。 1. 相似三角形的应用主要有两个方面:(1) 测高 测量不能到达两点间的距离,常构造相似三角形求解。(不能直接使用皮尺或刻度尺量的)(不能直接测量的两点间的距离) 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。(2) 测距课堂小结2. 解相似三角形实际问题的一般步骤:(1)审题。
(2)构建图形。
(3)利用相似解决问题。随堂练习 1. 铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m。 8 2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______。 4 3. △ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为 x 毫米。
因为PN∥BC,所以△APN∽ △ABC
所以 4. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)ADBCE┏┏0.8m5m10m?2.4m 5. 在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为90米,那么高楼的高度是多少米? 6. 为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 如图,测得BD=120m,DC=60m,EC=
50m,求河宽AB。解:∵∠B=∠C=90°,
∠ADB=∠EDC,
∴△ABD∽△ECD,
AB:EC=BD:DC,
AB=50×120÷60
=100(m)
已知左、右并排的两棵大树的高分别是
AB=8m和CD=12m,两树的根部的距离
BD=5m,一个身高1.6m的人沿着正
对这两棵树的一条水平直路ι
从左向右前进,当他与左边
较低的树的距离小于多少时,
就不能看到右边较高的树的顶
端点C?
设观察者眼晴的位置(视点)
为F,∠CFK和∠AFH分别是
观察点C、A的仰角,区域Ⅰ
和区域Ⅱ都在观察者看不到
的区域(盲区)之内。解:假设观察者从左向右走到点E时,他的眼睛的
位置点F与两棵树的顶端点A、C在一条直线上。
∵AB⊥ι,CD⊥ι,
∴AB∥CD,△AFH∽△CFK,
∴FH:FK=AH:CK,
即
,
解得FH=8.当他与左边较低的树的距离小
于8m时,就不能看到右边较高
的树的顶端点C。
—— 红杉世界上最高的楼
——台北101大楼怎样测量这些非常高大物体的高度?世界上最宽的河
——亚马孙河怎样测量河宽?利用三角形相似可以解决一些不能直接测量的物体的长度的问题 古希腊数学家、天文学家泰勒斯利用相似三角形的原理,测量金字塔的高度。DEA(F)BO2m3m201m解:太阳光是平行线, 因此∠BAO= ∠EDF又 ∠AOB= ∠DFE=90°
∴△ABO∽△DEF=BO == 134AFEBO┐┐还可以有其他方法测量吗?=△ABO∽△AEFOB =平面镜怎样测量旗杆的高度?6m1.2m1.6m物1高 :物2高 = 影1长 :影2长测高的方法 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决。 ∠P=∠P 分析:∵∠PQR=∠PST= 90° STPQRba得 PQ=90求河宽?∴ △PQR ∽△PST∴45m60m90m∴测距的方法 测量不能到达两点间的距离,常构造相似三角形求解。 1. 相似三角形的应用主要有两个方面:(1) 测高 测量不能到达两点间的距离,常构造相似三角形求解。(不能直接使用皮尺或刻度尺量的)(不能直接测量的两点间的距离) 测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决。(2) 测距课堂小结2. 解相似三角形实际问题的一般步骤:(1)审题。
(2)构建图形。
(3)利用相似解决问题。随堂练习 1. 铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高______m。 8 2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______。 4 3. △ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为 x 毫米。
因为PN∥BC,所以△APN∽ △ABC
所以 4. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)ADBCE┏┏0.8m5m10m?2.4m 5. 在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为90米,那么高楼的高度是多少米? 6. 为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 如图,测得BD=120m,DC=60m,EC=
50m,求河宽AB。解:∵∠B=∠C=90°,
∠ADB=∠EDC,
∴△ABD∽△ECD,
AB:EC=BD:DC,
AB=50×120÷60
=100(m)
已知左、右并排的两棵大树的高分别是
AB=8m和CD=12m,两树的根部的距离
BD=5m,一个身高1.6m的人沿着正
对这两棵树的一条水平直路ι
从左向右前进,当他与左边
较低的树的距离小于多少时,
就不能看到右边较高的树的顶
端点C?
设观察者眼晴的位置(视点)
为F,∠CFK和∠AFH分别是
观察点C、A的仰角,区域Ⅰ
和区域Ⅱ都在观察者看不到
的区域(盲区)之内。解:假设观察者从左向右走到点E时,他的眼睛的
位置点F与两棵树的顶端点A、C在一条直线上。
∵AB⊥ι,CD⊥ι,
∴AB∥CD,△AFH∽△CFK,
∴FH:FK=AH:CK,
即
,
解得FH=8.当他与左边较低的树的距离小
于8m时,就不能看到右边较高
的树的顶端点C。
