15.2.2添括号
图片预览








文档简介
课件22张PPT。添括号复习1.去括号的法则是什么?
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号。2.去括号(口答):解:引入:
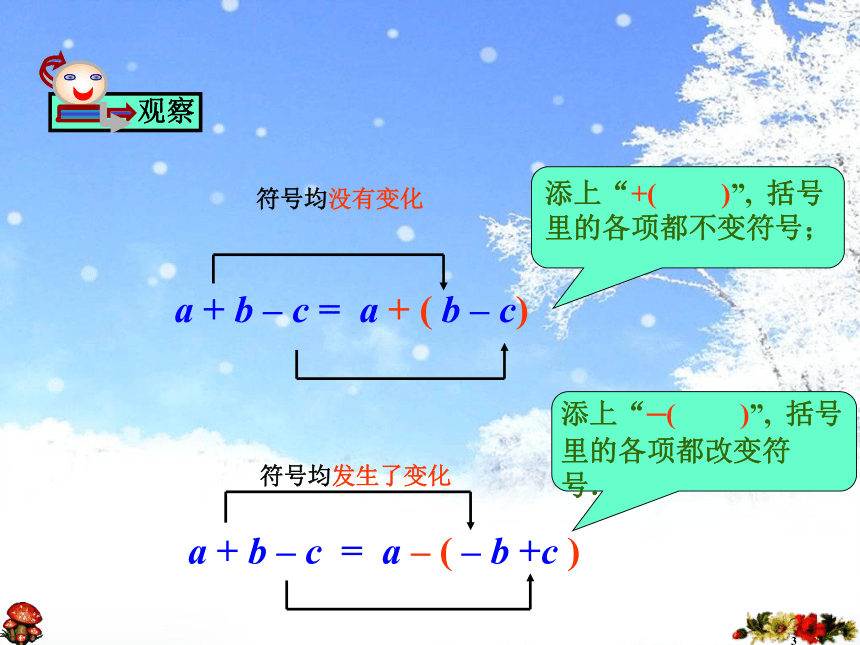
上面是根据去括号法则,由左边式子得右边式子,现在我们把上面四个式子反过来(1) a+b-c=a+(b-c)
(2) a-b-c=a+(-b-c)
(3) a+b-c=a-(-b+c)
(4) a-b+c=a-(b-c)3a + b – c = a + ( b – c)符号均没有变化 a + b – c = a – ( – b +c )符号均发生了变化 (1)a-b+c-d=a+( )
(2)a-b-c+d=a-( )
(3)a-b+c-d=a-b+( )
(4)a-b+c-d=-( )-b+c-db+c-dc-d-a+b-c+d针对性练习添括号法则 对添括号法则的理解及注意事项如下:(1)添括号是添上括号和括号前面的符号。也就是说,添括号时,括号前面的“+”或“-”也是新添的不是原来多项式的某一项的符号“移”出来的。(2)添括号的过程与去括号的过程正好相反,添括号是否正确,可用去括号检验。 总之。无论去括号还是添括号,只改变式子的形式,不改变式子的值,这就是多项式的恒等变形。“负”变“正”不变!!例1.在下列各式的括号内填上适当的项: (1)x3-3x2y+3xy2-y3=x3+( )
(2)2-x2+2xy-y2=2-( ) 评析:根据添括号法则,若括号前是“+”,括到括号里的各项都不变号,即保持原来的符号不变,如果第(1)小题。如果括号前是“-”号,括到括号里的各项都要变号,即“+”变“-”,“-”变“+”,如第(2)小题。注意“各项”是指括号里面“所有的项”。-3x2y+3xy2-y3x2-2xy+y2例 2.判断下列添括号是否正确(正确的打“∨”,错误的打“×”)(1)m-n-x+y=m-(n-x+y) ( )
(2)m-a+b-1=m+(a+b-1) ( )
(3)2x-y+z-1=-(2x+y-z+1) ( )
(4)x-y-z+1=(x-y)-(z-1) ( )×××∨m-(n+x-y)m+(-a+b-1)-(-2x+y-z+1)例3.不改变代数式a2-(2a+b+c)的值,把它括号前面的符号变为相反的符号,应为( ) (A)a2+(-2a+b+c) (B)a2+(-2a-b-c)
(C)a2+(-2a)+b+c (D)a2-(-2a-b-c)评析:此题既要用去括号,又要用添括号法则,即先去括号,再添括号,然后选择正确答案。B例4. 填空: 2xy2 – x3 – y3 + 3x2y
=+( )
= –( )
= 2xy2 – ( )+ 3x2y
= 2xy2 + ( )+ 3x2y
= 2xy2 – ( ) – x3 2xy2 – x3 – y3 + 3x2y– 2xy2 + x3 + y3 – 3x2yx3 + y3– x3 – y3y3 – 3x2y(1) 3x2 y2 – 2 x3 + y3
(2) – a3 + 2a2 – a +1
(3) 3x2 – 2xy2 + 2y2例5. 给下列多项式添括号,使它们的最高次项系数为正数.如: – x2 + x = –(x2 – x); x2 – x = + (x2 – x)= +( )= –( )= –( )= –( )93x2 y2 – 2 x3 + y3a3 – 2a2 + a – 1– 3x2 + 2xy2 – 2y22xy2– 3x2 – 2y2 把多项式x3-6x2y+12xy2-8y3+1,写成两个整式的和,使其中一个不含字母x。例6.[思考] 解: x3-6x2y+12xy2-8y3+1
=(x3-6x2y+12xy2)+(-8y3+1)添括号法则的应用 添括号一个最简单的应用就是简便计算,根据加法的交换律和结合律,把一些特殊的项括到括号里先计算,从而使整个式子的计算大为简便。
另外还可以按照题目的要求,把多项式中具有某些特征的项重新排列或分组,达到预定的要求,此时就要添括号了。例7. 化简求值:2x2y –3xy2 + 4x2y–5 xy2其中x=1,y=-1解:2x2y –3xy2 + 4x2y–5 xy2=(2x2y + 4x2y) –(3xy2 + 5 xy2)=6x2y–8xy2当x=1,y=-1时原式=6×12×(–1)–8×1×( –1 )2= –6–8= –14例8. 用简便方法计算:
(1)214a+47a+53a;(2)214a – 39a – 61a.7解:(1) 214a+47a+53a= 214a+(47a+53a)= 214a+100a= 314a(2) 214a – 39a – 61a=214a – (39a + 61a)=214a – 100a=114a例9.已知2x+3y-1=0,求3-6x-9y的值。解:∵2x+3y-1=0,∴2x+3y=1。
∴3-6x-9y=3-(6x+9y)=3-3(2x+3y)=3-3×1=0
答:所求代数式的值为0。评析:学习了添括号法则后,对于某些求值问题灵活应用添括号的方法,可化难为易。如本题,虽然没有给出x、y的取值,但利用添括号和整体代入,求值问题迎刃而解。注意体会和掌握这种方法。[练习] 已知3x2-x=1,求7-9x2+3x的值。解 7-9x2+3x=7-(9x2-3x)=7-3(3x2-x)=7-3×1=4例10.设x2+xy=3,xy+y2=-2,求2x2-xy-3y2的值。解:∵x2+xy=3,∴2(x2+xy)=6,即2x2+2xy=6
∴ 2x2-xy-3y2=2x2+2xy-3xy-3y2
=(2x2+2xy)-(3xy+3y2)
=(2x2+2xy)-3(xy+y2)
=6-3×(-2)=6+6=12评析:利用所给条件,对多项式进行拆项、重新分组是解此类题的关键。分组时要添括号,按添括号法则进行,注意符号的变化及分配律的应用。思考:已知a-b=6,c-b=5,求a-c的值.解 a-c=a-b+b-c=(a-b)-(c-b)=8-5=1例11.已知A=4x2-4xy+y2,B=x2+xy-5y2,求A-B。评析:本题产生错误的原因是把A、B代入所求式子时,丢掉了括号,导致后两项的符号错误。因为A、B表示两个多项式,它是一个整体,代入式子时必须用括号表示,尤其是括号前面是“-”时,如果丢掉了括号就会发生符号错误,今后遇到这类问题,一定要记住“添括号”。错解:A-B=4x2-4xy+y2-x2+xy-5y2=3x2-3xy-4y2正解:A-B=(4x2-4xy+y2)-(x2+xy-5y2)
=4x2-4xy+y2-x2-xy+5y2
=3x2-5xy+6y2易错题精讲 例12.求多项式x2-7x-2与-2x2+4x-1的差。解:(x2-7x-2)-(-2x2+4x-1)
= x2-7x-2+2x2-4x+1
=(x2+2x2)+(-7x-4x)+(-2+1)
=3x2-11x-1我们的收获……结合本堂课内容:我学会了……
我明白了……
我会用……
布置作业,巩固提高1.设x2-xy=5,xy+3y2=3,求x2-2xy-3y2的值。2. 求多项式2x2-xy+3y2与x2-xy-2y2的差。
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号。2.去括号(口答):解:引入:
上面是根据去括号法则,由左边式子得右边式子,现在我们把上面四个式子反过来(1) a+b-c=a+(b-c)
(2) a-b-c=a+(-b-c)
(3) a+b-c=a-(-b+c)
(4) a-b+c=a-(b-c)3a + b – c = a + ( b – c)符号均没有变化 a + b – c = a – ( – b +c )符号均发生了变化 (1)a-b+c-d=a+( )
(2)a-b-c+d=a-( )
(3)a-b+c-d=a-b+( )
(4)a-b+c-d=-( )-b+c-db+c-dc-d-a+b-c+d针对性练习添括号法则 对添括号法则的理解及注意事项如下:(1)添括号是添上括号和括号前面的符号。也就是说,添括号时,括号前面的“+”或“-”也是新添的不是原来多项式的某一项的符号“移”出来的。(2)添括号的过程与去括号的过程正好相反,添括号是否正确,可用去括号检验。 总之。无论去括号还是添括号,只改变式子的形式,不改变式子的值,这就是多项式的恒等变形。“负”变“正”不变!!例1.在下列各式的括号内填上适当的项: (1)x3-3x2y+3xy2-y3=x3+( )
(2)2-x2+2xy-y2=2-( ) 评析:根据添括号法则,若括号前是“+”,括到括号里的各项都不变号,即保持原来的符号不变,如果第(1)小题。如果括号前是“-”号,括到括号里的各项都要变号,即“+”变“-”,“-”变“+”,如第(2)小题。注意“各项”是指括号里面“所有的项”。-3x2y+3xy2-y3x2-2xy+y2例 2.判断下列添括号是否正确(正确的打“∨”,错误的打“×”)(1)m-n-x+y=m-(n-x+y) ( )
(2)m-a+b-1=m+(a+b-1) ( )
(3)2x-y+z-1=-(2x+y-z+1) ( )
(4)x-y-z+1=(x-y)-(z-1) ( )×××∨m-(n+x-y)m+(-a+b-1)-(-2x+y-z+1)例3.不改变代数式a2-(2a+b+c)的值,把它括号前面的符号变为相反的符号,应为( ) (A)a2+(-2a+b+c) (B)a2+(-2a-b-c)
(C)a2+(-2a)+b+c (D)a2-(-2a-b-c)评析:此题既要用去括号,又要用添括号法则,即先去括号,再添括号,然后选择正确答案。B例4. 填空: 2xy2 – x3 – y3 + 3x2y
=+( )
= –( )
= 2xy2 – ( )+ 3x2y
= 2xy2 + ( )+ 3x2y
= 2xy2 – ( ) – x3 2xy2 – x3 – y3 + 3x2y– 2xy2 + x3 + y3 – 3x2yx3 + y3– x3 – y3y3 – 3x2y(1) 3x2 y2 – 2 x3 + y3
(2) – a3 + 2a2 – a +1
(3) 3x2 – 2xy2 + 2y2例5. 给下列多项式添括号,使它们的最高次项系数为正数.如: – x2 + x = –(x2 – x); x2 – x = + (x2 – x)= +( )= –( )= –( )= –( )93x2 y2 – 2 x3 + y3a3 – 2a2 + a – 1– 3x2 + 2xy2 – 2y22xy2– 3x2 – 2y2 把多项式x3-6x2y+12xy2-8y3+1,写成两个整式的和,使其中一个不含字母x。例6.[思考] 解: x3-6x2y+12xy2-8y3+1
=(x3-6x2y+12xy2)+(-8y3+1)添括号法则的应用 添括号一个最简单的应用就是简便计算,根据加法的交换律和结合律,把一些特殊的项括到括号里先计算,从而使整个式子的计算大为简便。
另外还可以按照题目的要求,把多项式中具有某些特征的项重新排列或分组,达到预定的要求,此时就要添括号了。例7. 化简求值:2x2y –3xy2 + 4x2y–5 xy2其中x=1,y=-1解:2x2y –3xy2 + 4x2y–5 xy2=(2x2y + 4x2y) –(3xy2 + 5 xy2)=6x2y–8xy2当x=1,y=-1时原式=6×12×(–1)–8×1×( –1 )2= –6–8= –14例8. 用简便方法计算:
(1)214a+47a+53a;(2)214a – 39a – 61a.7解:(1) 214a+47a+53a= 214a+(47a+53a)= 214a+100a= 314a(2) 214a – 39a – 61a=214a – (39a + 61a)=214a – 100a=114a例9.已知2x+3y-1=0,求3-6x-9y的值。解:∵2x+3y-1=0,∴2x+3y=1。
∴3-6x-9y=3-(6x+9y)=3-3(2x+3y)=3-3×1=0
答:所求代数式的值为0。评析:学习了添括号法则后,对于某些求值问题灵活应用添括号的方法,可化难为易。如本题,虽然没有给出x、y的取值,但利用添括号和整体代入,求值问题迎刃而解。注意体会和掌握这种方法。[练习] 已知3x2-x=1,求7-9x2+3x的值。解 7-9x2+3x=7-(9x2-3x)=7-3(3x2-x)=7-3×1=4例10.设x2+xy=3,xy+y2=-2,求2x2-xy-3y2的值。解:∵x2+xy=3,∴2(x2+xy)=6,即2x2+2xy=6
∴ 2x2-xy-3y2=2x2+2xy-3xy-3y2
=(2x2+2xy)-(3xy+3y2)
=(2x2+2xy)-3(xy+y2)
=6-3×(-2)=6+6=12评析:利用所给条件,对多项式进行拆项、重新分组是解此类题的关键。分组时要添括号,按添括号法则进行,注意符号的变化及分配律的应用。思考:已知a-b=6,c-b=5,求a-c的值.解 a-c=a-b+b-c=(a-b)-(c-b)=8-5=1例11.已知A=4x2-4xy+y2,B=x2+xy-5y2,求A-B。评析:本题产生错误的原因是把A、B代入所求式子时,丢掉了括号,导致后两项的符号错误。因为A、B表示两个多项式,它是一个整体,代入式子时必须用括号表示,尤其是括号前面是“-”时,如果丢掉了括号就会发生符号错误,今后遇到这类问题,一定要记住“添括号”。错解:A-B=4x2-4xy+y2-x2+xy-5y2=3x2-3xy-4y2正解:A-B=(4x2-4xy+y2)-(x2+xy-5y2)
=4x2-4xy+y2-x2-xy+5y2
=3x2-5xy+6y2易错题精讲 例12.求多项式x2-7x-2与-2x2+4x-1的差。解:(x2-7x-2)-(-2x2+4x-1)
= x2-7x-2+2x2-4x+1
=(x2+2x2)+(-7x-4x)+(-2+1)
=3x2-11x-1我们的收获……结合本堂课内容:我学会了……
我明白了……
我会用……
布置作业,巩固提高1.设x2-xy=5,xy+3y2=3,求x2-2xy-3y2的值。2. 求多项式2x2-xy+3y2与x2-xy-2y2的差。
