4．1生活中的立体图形

【学习目的】
能辨别生活中所遇到的立体图形的区别；能正确识别和判断具体的图形，从而体验数学概念的抽象和形成过程。
【典型例题】
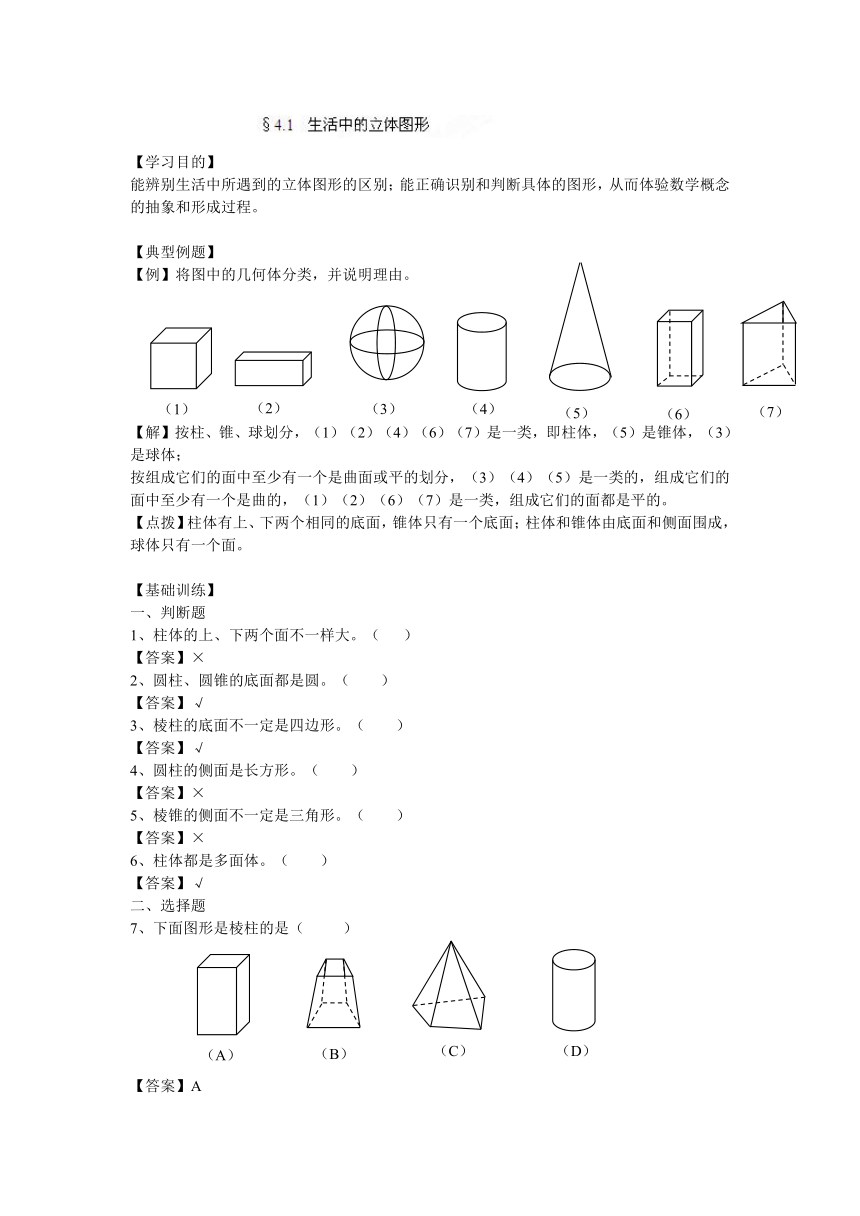
【例】将图中的几何体分类，并说明理由。
【解】按柱、锥、球划分，（1）（2）（4）（6）（7）是一类，即柱体，（5）是锥体，（3）是球体；
按组成它们的面中至少有一个是曲面或平的划分，（3）（4）（5）是一类的，组成它们的面中至少有一个是曲的，（1）（2）（6）（7）是一类，组成它们的面都是平的。
【点拨】柱体有上、下两个相同的底面，锥体只有一个底面；柱体和锥体由底面和侧面围成，球体只有一个面。
【基础训练】
一、判断题
1、柱体的上、下两个面不一样大。（ ）
【答案】×
2、圆柱、圆锥的底面都是圆。（ ）
【答案】√
3、棱柱的底面不一定是四边形。（ ）
【答案】√
4、圆柱的侧面是长方形。（ ）
【答案】×
5、棱锥的侧面不一定是三角形。（ ）
【答案】×
6、柱体都是多面体。（ ）
【答案】√
二、选择题
7、下面图形是棱柱的是（ ）
【答案】A
三、填表
8、完成下表，你能得到什么结论？
多面体
面数（F）
顶点数（V）
棱边数（E）
F+V
（F+V）－E
1
四面体
2
立方体
3
八面体
4
十二面体
5
二十面体
6
三棱柱
7
正四棱柱
8
正四棱锥
你得到的结论： 。
【答案】填表略，（F+V）－E=2
【拓展训练】
9、三棱柱有9条棱，6个顶点，5个面；三棱锥有6条棱，4个顶点，4个面；四棱柱有12条棱，8个顶点，6个面；四棱锥有8条棱，5个顶点，5个面等等。问能否组成一个有24条棱，10个面，15个顶点的多面体？为什么？
【答案】不能，因为这个多面体的棱数、面数、顶点数不满足（F+V）－E=2。
【探究实践】
10、一个四棱柱被一刀切去一个角，请你画图说明剩下的部分的形状。
【答案】略