必修二第一章空间几何体单元测试四(附答案)
文档属性
| 名称 | 必修二第一章空间几何体单元测试四(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 323.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-15 13:57:03 | ||
图片预览




文档简介
必修二第一章空间几何体单元测试四(附答案)
学校:___________姓名:___________班级:___________考号:___________
1.下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是( )
A.(1)(2) B.(2)(3) C. (3)(4) D. (1)(4)
2.一个体积为的正三棱柱的三视图如图所示,则这个三棱柱的侧视图的面积为 ( )
A. B.8 C. D.12
3.在平行四边形ABCD中,,若将其沿BD折成直二面角A-BD-C,则A-BCD的外接球的表面积为( )
A B C d.
4.已知直棱柱的底面是边长为3的正三角形,高为2,则其外接球的表面积( )
A.6仔 B.8仔 C.12仔 D.16仔
5.长方体的长,宽,高分别是3,2,1,则该长方体的体对角线是( )
A. B. C. D.
6.一个体积为的正方体的顶点都在球面上,则球的体积是( )
A. B. C. D.
7. 如果一个水平放置的图形的斜二测直观图是一个底面为,腰和上底均为的等腰梯形,那么原平面图形的面积是( )
A. B. C. D.
8.一个几何体的三视图如图所示,则该几何体是( )
A.圆柱B.四棱柱C.圆台D.棱台
9.设地球是半径为R的球,地球上A、B两地都在北纬45°的纬线上,A在东经20°、B在东经110°的经线上,则A、B两地的球面距离是 ( )
A. B. C. D.
10.如图,正三棱柱的棱长和底面边长均为2,主视图是
边长为2的正方形,则左视图的面积为( )
A. B. C. D.
二、填空题
11.如图是一个几何体的三视图,若它的体积是,则a=________.
12.已知某个几何体的三视图如图所示,根据图中标出的尺寸,则这个几何体的体积是 .
13.在平面内,三角形的面积为S,周长为C,则它的内切圆的半径.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=___________。
14.在的二面角内放入一个球,球与该二面角的两个半平面分别切于两点A,B,且A、B两点的球面距离为2cm,则该球的半径为 .
15.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为2,2,3,则此球的表面积为 .
16.四面体ABCD中,共顶点A的三条棱两两相互垂直,且其长分别为,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
三、解答题
17.(本小题满分14分)
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为。
求f(h)的表达式,并写出h的取值范围是 ;
求三个圆柱体积之和V的最大值;
18.如图,在矩形中,,沿对角线把折起到位置,且在面内的射影恰好落在上
(1)求证: ;
(2)求与平面所成的角的正弦值.
19.如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
求BC1与平面B1C1EF所成的角的正弦值.
20.如图,在四棱锥P—ABCD中,底面是边长为的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=,M,N分别为PB,PD的中点.
(Ⅰ)证明:MN∥平面ABCD;
(Ⅱ) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值.
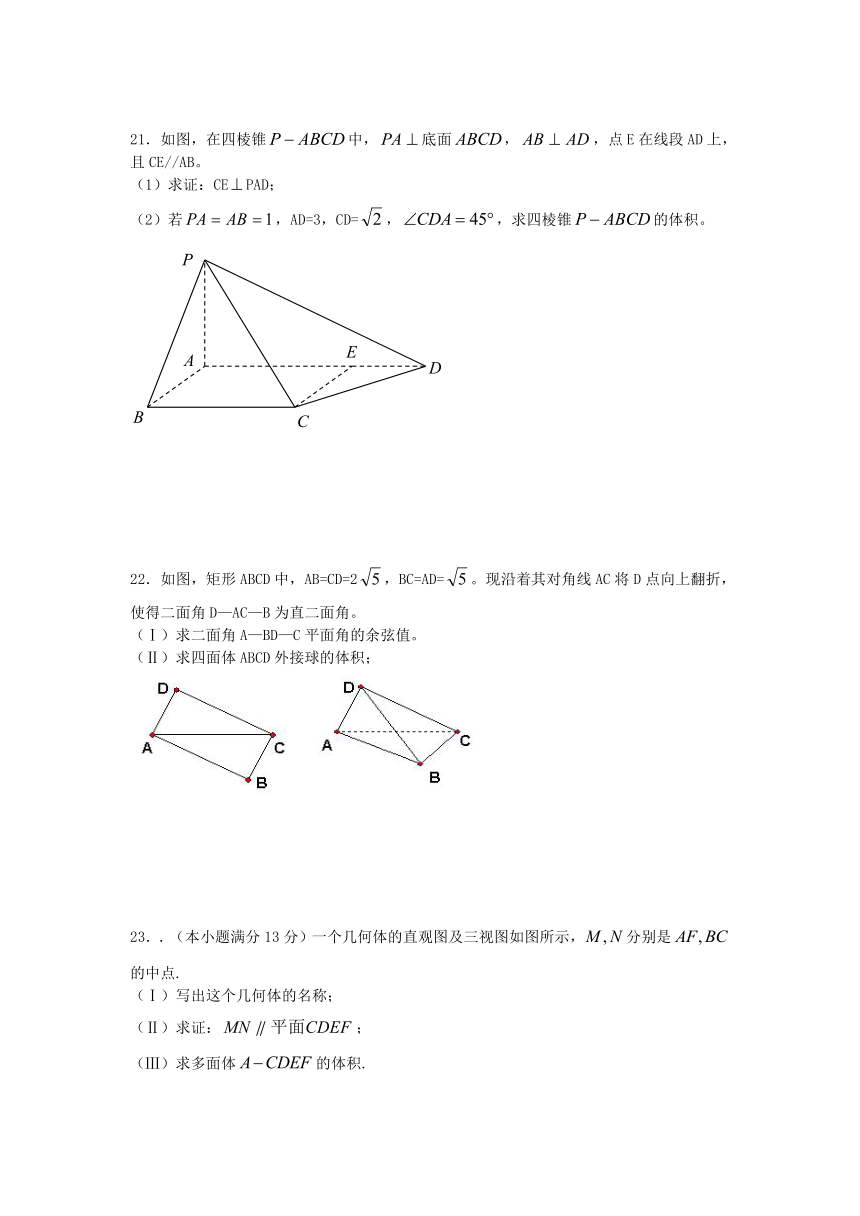
21.如图,在四棱锥中,底面,,点E在线段AD上,且CE//AB。
(1)求证:CEPAD;
(2)若,AD=3,CD=,,求四棱锥的体积。
22.如图,矩形ABCD中,AB=CD=2,BC=AD=。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
(Ⅰ)求二面角A—BD—C平面角的余弦值。
(Ⅱ)求四面体ABCD外接球的体积;
23..(本小题满分13分)一个几何体的直观图及三视图如图所示,分别是的中点.
(Ⅰ)写出这个几何体的名称;
(Ⅱ)求证:;
(Ⅲ)求多面体的体积.
24.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P—EFGH,下半部分是长方体ABCD—EFGH,图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线BD⊥平面PEG
25.本题满分13分如图,三角形ABC中,AC=BC=,ABED是边长为1
的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(I)求证:GF//底面ABC;
(Ⅱ)求证:AC⊥平面EBC;
(Ⅲ)求几何体ADEBC的体积V.
参考答案
1.D
2.A
3.C
4.D
5.A
6.A
7.A
8.C
9.C
10.B
11.
12.
13.
14.3cm
15.
16.
17.(1)的取值范围是;⑵三个圆柱体积和的最大值为.
18.(1)证明略 (2)与平面所成角的正弦值为.
19.(3)
20.(Ⅰ)略(Ⅱ) .
21.(2)5/ 6
22.如图,过点D、B分别向AC引垂线,垂足分别为E、F。易知AE=CF=1,EF=3,DE=BF=2。又DE⊥AC,AC=面ACD∩面ABC,二面角D—AC—B为直二面角,所以DE⊥平面ABC,又因为BF平面ABC,所以DE⊥BF。故DE、AC、BF两两垂直。如图以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系.
则各点的如下A(0,-4,0),B(2,0,0),C(0,1,0),D(0,-3,2). (3分)
(1) =(0,1,2),=(2,4,0),=(-2,1,0),=(0,-4,2)
设平面ABD的法向量为=(x,y,1),则,
即=(4,-2,1)
设平面BCD的法向量为=(1,b,c),则
即=(1,2,4)
Cos<,>==. 21世纪教育网
由图形知二面角A—BD—C平面角的余弦值为-. (8分)
(2)设O为AC的中点,∵⊿ABC与⊿ADC都为直角三角形,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心.
∴四面体ABCD的体积
23.解:(Ⅰ)这个几何体是底面是直角三角形的直三棱柱(写成直三棱柱也给分)…2分
(Ⅱ)解法一:(面面平行线面平行)
由三视图可知,
……………………………………………………………4分
取的中点连,
由、分别为、的中点可得
又,
∴,…………………………………6分
又
∴
而,∴………………………………8分
解法二:(线线平行线面平行)
连续,则,……………………………4分
∵,∴………………………………………………6分
又
∴…………………………………………………8分
(Ⅲ)取的中点.
∵,∴,在直三棱柱中
∴……………………………………………………9分
∴多面体是以为高,以矩形为底面的棱锥…………10分
在中,………………………………11分
∴棱锥的体积…………13分
24.
解:(1)侧视图同正视图,如下图所示。
(2)该安全标识墩的体积为:
=
(3)如图,连结EG,HF及BD,EG与HF相交于O,连结PO,
由正四棱锥的性质可知,PO⊥平面EFGH,∴PO⊥HF
又EG⊥HF ∴HF⊥平面PEG
又BD∥HF ∴BD⊥平面PEG
25.解:(I)证法一:取BE的中点H,连结HF、GH,(如图1)
∵G、F分别是EC和BD的中点
∴HG//BC,HF//DE,……………… 2分
又∵ADEB为正方形 ∴DE//AB,从而HF//AB
∴HF//平面ABC,HG//平面ABC, HF∩HG=H,
∴平面HGF//平面ABC
∴GF//平面ABC………………4分
(Ⅱ)∵ADEB为正方形,∴EB⊥AB,∴GF//平面AB………………5分
又∵平面ABED⊥平面ABC,∴BE⊥平面ABC ………………6分
∴BE⊥AC
又∵CA2+CB2=AB2
∴AC⊥BC,
∵BC∩BE=B,
∴AC⊥平面BCE ………………8分
(Ⅲ)连结CN,因为AC=BC,∴CN⊥AB, ……………… 9分
又平面ABED⊥平面ABC,CN平面ABC,∴CN⊥平面ABED。……………… 10分
∵三角形ABC是等腰直角三角形,∴, ………………11分
∵C—ABED是四棱锥,
∴VC—ABED= ………………13分
学校:___________姓名:___________班级:___________考号:___________
1.下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是( )
A.(1)(2) B.(2)(3) C. (3)(4) D. (1)(4)
2.一个体积为的正三棱柱的三视图如图所示,则这个三棱柱的侧视图的面积为 ( )
A. B.8 C. D.12
3.在平行四边形ABCD中,,若将其沿BD折成直二面角A-BD-C,则A-BCD的外接球的表面积为( )
A B C d.
4.已知直棱柱的底面是边长为3的正三角形,高为2,则其外接球的表面积( )
A.6仔 B.8仔 C.12仔 D.16仔
5.长方体的长,宽,高分别是3,2,1,则该长方体的体对角线是( )
A. B. C. D.
6.一个体积为的正方体的顶点都在球面上,则球的体积是( )
A. B. C. D.
7. 如果一个水平放置的图形的斜二测直观图是一个底面为,腰和上底均为的等腰梯形,那么原平面图形的面积是( )
A. B. C. D.
8.一个几何体的三视图如图所示,则该几何体是( )
A.圆柱B.四棱柱C.圆台D.棱台
9.设地球是半径为R的球,地球上A、B两地都在北纬45°的纬线上,A在东经20°、B在东经110°的经线上,则A、B两地的球面距离是 ( )
A. B. C. D.
10.如图,正三棱柱的棱长和底面边长均为2,主视图是
边长为2的正方形,则左视图的面积为( )
A. B. C. D.
二、填空题
11.如图是一个几何体的三视图,若它的体积是,则a=________.
12.已知某个几何体的三视图如图所示,根据图中标出的尺寸,则这个几何体的体积是 .
13.在平面内,三角形的面积为S,周长为C,则它的内切圆的半径.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R=___________。
14.在的二面角内放入一个球,球与该二面角的两个半平面分别切于两点A,B,且A、B两点的球面距离为2cm,则该球的半径为 .
15.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为2,2,3,则此球的表面积为 .
16.四面体ABCD中,共顶点A的三条棱两两相互垂直,且其长分别为,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
三、解答题
17.(本小题满分14分)
在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为。
求f(h)的表达式,并写出h的取值范围是 ;
求三个圆柱体积之和V的最大值;
18.如图,在矩形中,,沿对角线把折起到位置,且在面内的射影恰好落在上
(1)求证: ;
(2)求与平面所成的角的正弦值.
19.如图,在侧棱垂直底面的四棱柱ABCD-A1B1C1D1中,AD∥BC,AD⊥AB,AB=。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
求BC1与平面B1C1EF所成的角的正弦值.
20.如图,在四棱锥P—ABCD中,底面是边长为的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=,M,N分别为PB,PD的中点.
(Ⅰ)证明:MN∥平面ABCD;
(Ⅱ) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值.
21.如图,在四棱锥中,底面,,点E在线段AD上,且CE//AB。
(1)求证:CEPAD;
(2)若,AD=3,CD=,,求四棱锥的体积。
22.如图,矩形ABCD中,AB=CD=2,BC=AD=。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
(Ⅰ)求二面角A—BD—C平面角的余弦值。
(Ⅱ)求四面体ABCD外接球的体积;
23..(本小题满分13分)一个几何体的直观图及三视图如图所示,分别是的中点.
(Ⅰ)写出这个几何体的名称;
(Ⅱ)求证:;
(Ⅲ)求多面体的体积.
24.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P—EFGH,下半部分是长方体ABCD—EFGH,图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线BD⊥平面PEG
25.本题满分13分如图,三角形ABC中,AC=BC=,ABED是边长为1
的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(I)求证:GF//底面ABC;
(Ⅱ)求证:AC⊥平面EBC;
(Ⅲ)求几何体ADEBC的体积V.
参考答案
1.D
2.A
3.C
4.D
5.A
6.A
7.A
8.C
9.C
10.B
11.
12.
13.
14.3cm
15.
16.
17.(1)的取值范围是;⑵三个圆柱体积和的最大值为.
18.(1)证明略 (2)与平面所成角的正弦值为.
19.(3)
20.(Ⅰ)略(Ⅱ) .
21.(2)5/ 6
22.如图,过点D、B分别向AC引垂线,垂足分别为E、F。易知AE=CF=1,EF=3,DE=BF=2。又DE⊥AC,AC=面ACD∩面ABC,二面角D—AC—B为直二面角,所以DE⊥平面ABC,又因为BF平面ABC,所以DE⊥BF。故DE、AC、BF两两垂直。如图以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系.
则各点的如下A(0,-4,0),B(2,0,0),C(0,1,0),D(0,-3,2). (3分)
(1) =(0,1,2),=(2,4,0),=(-2,1,0),=(0,-4,2)
设平面ABD的法向量为=(x,y,1),则,
即=(4,-2,1)
设平面BCD的法向量为=(1,b,c),则
即=(1,2,4)
Cos<,>==. 21世纪教育网
由图形知二面角A—BD—C平面角的余弦值为-. (8分)
(2)设O为AC的中点,∵⊿ABC与⊿ADC都为直角三角形,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心.
∴四面体ABCD的体积
23.解:(Ⅰ)这个几何体是底面是直角三角形的直三棱柱(写成直三棱柱也给分)…2分
(Ⅱ)解法一:(面面平行线面平行)
由三视图可知,
……………………………………………………………4分
取的中点连,
由、分别为、的中点可得
又,
∴,…………………………………6分
又
∴
而,∴………………………………8分
解法二:(线线平行线面平行)
连续,则,……………………………4分
∵,∴………………………………………………6分
又
∴…………………………………………………8分
(Ⅲ)取的中点.
∵,∴,在直三棱柱中
∴……………………………………………………9分
∴多面体是以为高,以矩形为底面的棱锥…………10分
在中,………………………………11分
∴棱锥的体积…………13分
24.
解:(1)侧视图同正视图,如下图所示。
(2)该安全标识墩的体积为:
=
(3)如图,连结EG,HF及BD,EG与HF相交于O,连结PO,
由正四棱锥的性质可知,PO⊥平面EFGH,∴PO⊥HF
又EG⊥HF ∴HF⊥平面PEG
又BD∥HF ∴BD⊥平面PEG
25.解:(I)证法一:取BE的中点H,连结HF、GH,(如图1)
∵G、F分别是EC和BD的中点
∴HG//BC,HF//DE,……………… 2分
又∵ADEB为正方形 ∴DE//AB,从而HF//AB
∴HF//平面ABC,HG//平面ABC, HF∩HG=H,
∴平面HGF//平面ABC
∴GF//平面ABC………………4分
(Ⅱ)∵ADEB为正方形,∴EB⊥AB,∴GF//平面AB………………5分
又∵平面ABED⊥平面ABC,∴BE⊥平面ABC ………………6分
∴BE⊥AC
又∵CA2+CB2=AB2
∴AC⊥BC,
∵BC∩BE=B,
∴AC⊥平面BCE ………………8分
(Ⅲ)连结CN,因为AC=BC,∴CN⊥AB, ……………… 9分
又平面ABED⊥平面ABC,CN平面ABC,∴CN⊥平面ABED。……………… 10分
∵三角形ABC是等腰直角三角形,∴, ………………11分
∵C—ABED是四棱锥,
∴VC—ABED= ………………13分
