2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.1.2全概率公式课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.1.2全概率公式课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 17:18:52 | ||
图片预览





文档简介
(共17张PPT)
7.1.2 全概率公式
1.求条件概率的方法
(1)减缩样本空间法:
(2)条件概率定义法:
设P(A)>0,则
(3)设B和 互为对立事件,则
2.条件概率的性质:
(2)如果B和C是两个互斥事件,则
请看课本P48:练习2,3
一、温故知新
1.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天的空气质量为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75
C.0.6 D.0.45
A
热身训练——回顾旧知:
2.一个盒子中有6个白球,4个黑球,从中不放回地每次任取1只,连取2次,则第一次取得白球的概率是________,第一次、第二次都取得白球的概率是________
热身训练——回顾旧知:
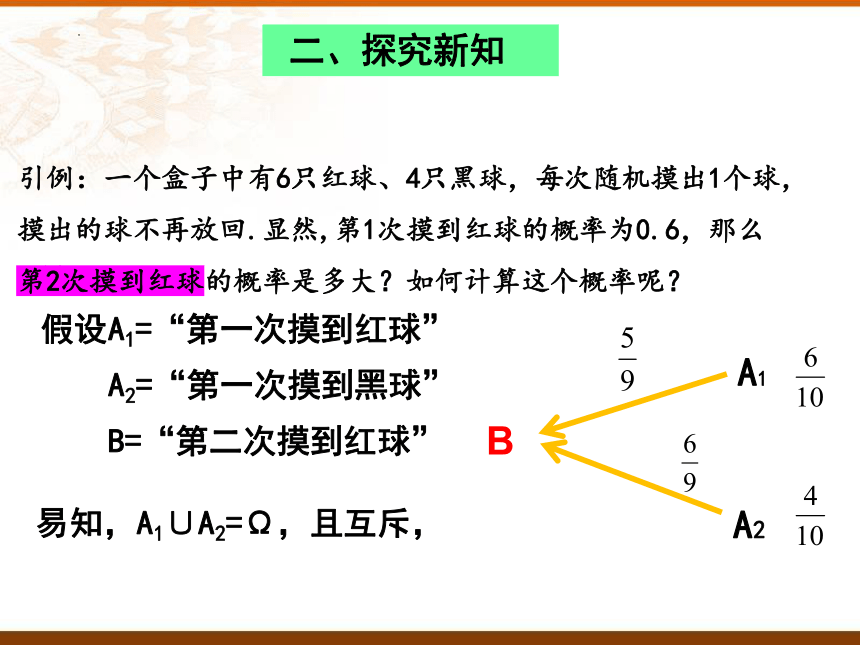
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
假设A1=“第一次摸到红球”
A2=“第一次摸到黑球”
B=“第二次摸到红球”
A2
A1
B
易知,A1∪A2=Ω,且互斥,
二、探究新知
A2
A1
B
二、探究新知
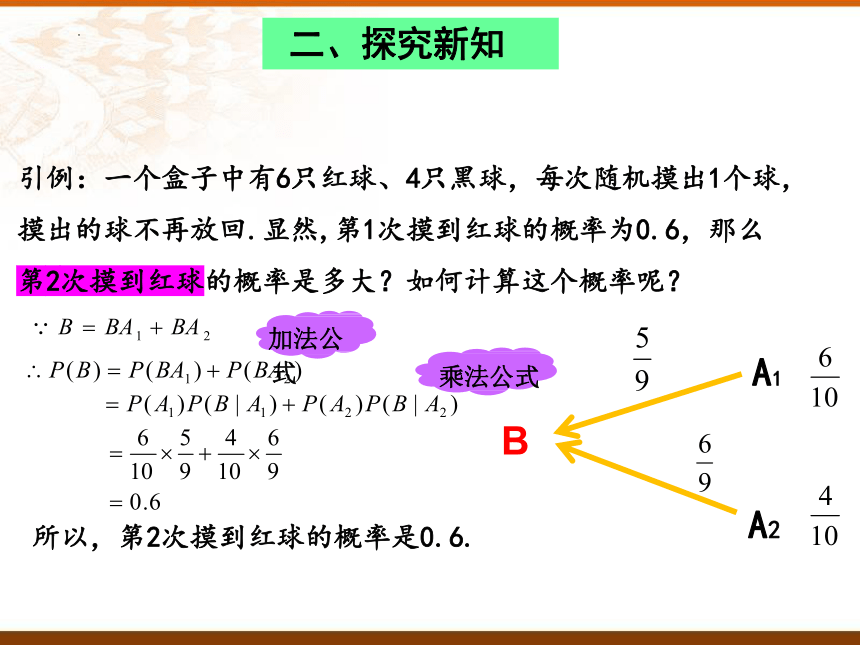
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
A2
A1
B
所以,第2次摸到红球的概率是0.6.
加法公式
乘法公式
二、探究新知
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式,求得这个复杂事件的概率.
B
1.全概率公式
三、巩固新知
例1:
解:
例2:
解:
解:
例2:
思考:
例2:
解:
2*.贝叶斯公式
四、课堂小结
1.全概率公式
2*.贝叶斯公式
1.甲袋里有5只白球,7只红球,乙袋里有4只白球,2只红球,从两个袋中任取一袋,然后从所取到的袋中任取一球,则取到的球是白球的概率为_______
学以致用:
2.李老师一家要外出游玩几天,家里有一盆花交给邻居帮助照顾,如果这几天内邻居记得浇水,那么花存活的概率为0.8,如果这几天邻居忘记浇水,那么花存活的概率为0.3.假设李老师对邻居不了解,即可以认为邻居记得和忘记浇水的概率均为0.5,几天后李老师回来发现花还活着,则邻居记得浇水的概率为________
学以致用:
7.1.2 全概率公式
1.求条件概率的方法
(1)减缩样本空间法:
(2)条件概率定义法:
设P(A)>0,则
(3)设B和 互为对立事件,则
2.条件概率的性质:
(2)如果B和C是两个互斥事件,则
请看课本P48:练习2,3
一、温故知新
1.某地区空气质量监测资料表明,一天的空气质量为优良的概率是0.75,连续两天的空气质量为优良的概率是0.6,已知某天的空气质量为优良,则随后一天的空气质量为优良的概率是 ( )
A.0.8 B.0.75
C.0.6 D.0.45
A
热身训练——回顾旧知:
2.一个盒子中有6个白球,4个黑球,从中不放回地每次任取1只,连取2次,则第一次取得白球的概率是________,第一次、第二次都取得白球的概率是________
热身训练——回顾旧知:
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
假设A1=“第一次摸到红球”
A2=“第一次摸到黑球”
B=“第二次摸到红球”
A2
A1
B
易知,A1∪A2=Ω,且互斥,
二、探究新知
A2
A1
B
二、探究新知
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
A2
A1
B
所以,第2次摸到红球的概率是0.6.
加法公式
乘法公式
二、探究新知
引例:一个盒子中有6只红球、4只黑球,每次随机摸出1个球,摸出的球不再放回.显然,第1次摸到红球的概率为0.6,那么第2次摸到红球的概率是多大?如何计算这个概率呢?
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式,求得这个复杂事件的概率.
B
1.全概率公式
三、巩固新知
例1:
解:
例2:
解:
解:
例2:
思考:
例2:
解:
2*.贝叶斯公式
四、课堂小结
1.全概率公式
2*.贝叶斯公式
1.甲袋里有5只白球,7只红球,乙袋里有4只白球,2只红球,从两个袋中任取一袋,然后从所取到的袋中任取一球,则取到的球是白球的概率为_______
学以致用:
2.李老师一家要外出游玩几天,家里有一盆花交给邻居帮助照顾,如果这几天内邻居记得浇水,那么花存活的概率为0.8,如果这几天邻居忘记浇水,那么花存活的概率为0.3.假设李老师对邻居不了解,即可以认为邻居记得和忘记浇水的概率均为0.5,几天后李老师回来发现花还活着,则邻居记得浇水的概率为________
学以致用:
