最新人教版七年级上数学第四章几何图形初步导学案
文档属性
| 名称 | 最新人教版七年级上数学第四章几何图形初步导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 127.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-16 10:17:26 | ||
图片预览




文档简介
第四章 几何图形初步
课题 4.1.1认识几何图形(1)
课型:新课
学时:1学时
主备人:廖晓阳
审阅人:黄坤权 廖晓阳 周飞 费光锦 刘国芬 苏国庆 吴诗言
一.目标:
1、通过观察生活中的大量图片或实物,经历把实物抽象成几何图形的过程;
2、能由实物形状想象出几何图形,由几何图形想象出实物形状;
3、能识别一些简单几何体,正确区分平面图形与立体图形。
二预习热身
同学们,你仔细观察过我们生活的世界吗?从城市宏伟的建筑到乡村简朴的住宅,从四通八达的立交桥到街头巷尾的交通标志,从古老的剪纸艺术到现代化的城市雕塑,从自然界形态各异的动物到北京的申奥标志……,包含着形态各异的图形。图形的世界是丰富多彩的!那就让我们走进图象的世界去看看吧。
三.活动探究
活动1.(1)仔细观察图4.1-1,让同学们感受是丰富多彩的图形世界;
(2)出示一个长方体的纸盒,让同学们观察图4.1-2回答问题:
从整体上看,它的形状是什么?从不同侧面看,你看到了什么图形?只看棱、顶点等局部,你又看到了什么?
我们见过的长方形、圆柱、圆锥、球、圆、线段、点,以及小学学习过的三角形、四边形等,都是从形形色色的物体外形中得出的。我们把这些图形称为几何图形。
注意:当我们关注物体的形状、大小和位置时,得出了几何图形,它是数学研究的主要对象之一,而物体的颜色、重量、材料等则是其它学科所关注的。
活动2.
思考第115页思考题并出示实物(如茶叶、地球仪、字典及魔方等)及多媒体演示(如谷堆、帐篷、金字塔等),它们与我们学过的哪些图形相类似?
长方体、正方体、球、圆柱、圆锥等它们各部分不都在同一平面内,它们是立体图形。
想一想
生活中还有哪些物体的形状类似于这些立体图形呢?
思考:课本115页图4.1-4中实物的形状对应哪些立体图形?把相应的实物与图形用线连起来。
活动3.
平面图形的概念
线段、角、三角形、长方形、圆等它们的各部分都在同一平面内,它们是平面图形。
思考:课本116页图4.1-5的图中包含哪些简单的平面图形?
请再举出一些平面图形的例子。
长方形、圆、正方形、三角形、……。
思考:立体图形与平面图形是两类不同的几何图形,它们的区别在哪里?它们有什么联系?
立体图形的各部分不都在同一平面内,而平面图形的各部分都在同一平面内;
立体图形中某些部分是平面图形。
四、盘点提升
你在本课中收获了什么?还有疑问吗?
1、
2、平面图形与立体图形的关系:
立体图形的各部分不都在同一平面内,而平面图形的各部分都在同一平面内;
立体图形中某些部分是平面图形。
五、达标检测
1.下列几种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;⑥球.其中属于立体图形的是( )
A. ①②③; B. ③④⑤; C. ① ③⑤; D. ③④⑤⑥
2.课本116页练习
课题4.1.1几何图形(2)
课型:新课
学时:1学时
一.目标:
1.经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果,了解为什么要从不同方向看;
2.能画出从不同方向看一些基本几何体(直棱柱、圆柱、圆锥、球)以及它们的简单组合得到的平面图形;
3.识别一些基本几何体(直棱柱、圆柱、圆锥、球)以及它们的简单组合得到的平面图形
4.画出从正面、左面、上面看正方体及简单组合体的平面图形
二.引入
多媒体演示庐山景观,请学生背诵苏东坡《题西林壁》并说说诗中意境。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
从数学的角度来理解是什么意思呢?
三.活动探究
活动1
1.说一说:分别从正面、左面、上面观察乒乓球、粉笔盒、茶叶盒,各能得到什么平面图形?(出示实物)
2.画一画:长方体、圆锥分别从正面、左面、上面观察,各能得到什么图形?试着画一画.(出示实物)这样,我们将立体图形转化成了平面图形
活动2.
从正面、左面、上面观察得到的平面图形你能画出来吗?(117页图4.1-7)
小组合作学习,动手画一画,并进行展示
探究:分别从正面、左面、上面观察课本117页图4.1-8这个图形,分别画出得到的平面图形。
活动3.
【课堂练习】:
课本118页练习1、
四.盘点提升:
1.本节课我们主要学习了什么?
2. 本节课我们有哪些收获?
3.你还有什么没有解决的问题?
五.达标检测
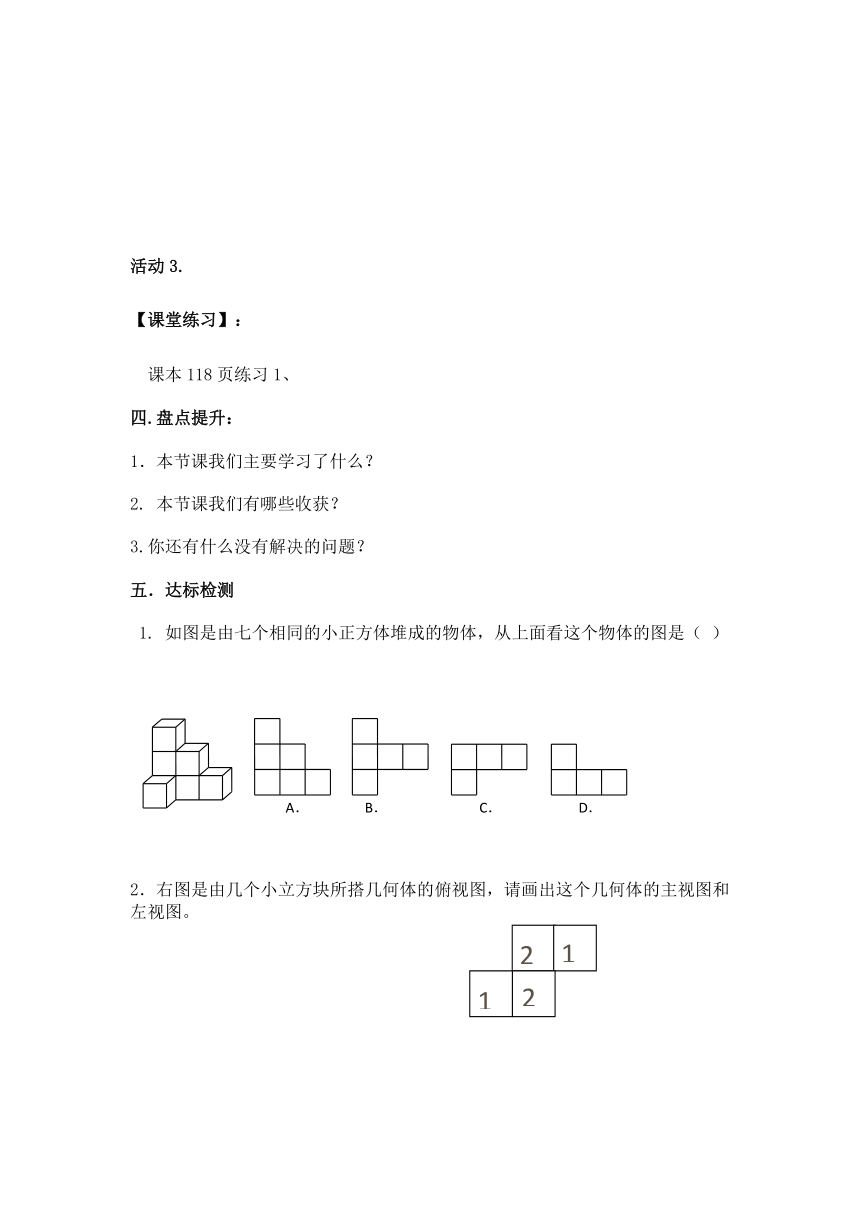
1. 如图是由七个相同的小正方体堆成的物体,从上面看这个物体的图是( )
2.右图是由几个小立方块所搭几何体的俯视图,请画出这个几何体的主视图和左视图。
【总结反思】:
课题4.1.1几何图形(3)
课型:新课
学时:1学时
一.目标:
1.能直观认识立体图形和展开图,了解研究立体图形方法。
2.通过观察和动手操作,经历和体验平面图形和立体图形相互转换的过程,培养动手操作能力,初步建立空间观念,发展几何直觉。
3.了解基本几何体与其展开图之间的关系,体会一个立体按照不同方式展开可得到不同的平面展开图。
4.正确判断哪些平面图形可以折叠为立体图形;某个立体图形的展开图可以是哪些平面图形
二.预习热身
我们把一些像墨水瓶盒、粉笔盒这样的纸盒沿它的表面适当剪开,可以展平成平面图形。这样的平面图形叫做相应立体图形的展开图。
你知道长方体、圆柱、圆锥和三棱柱的展开图是什么样子的吗?想象一下。
三.活动探究
活动1.探究立体图形的展开图
1、试一试:在你想象的基础上,请将准备好的长方体、圆柱、圆锥和三棱柱的纸盒剪开展平,看看与下面的展开图一样吗?
圆柱 圆锥 三棱柱 长方体
思考:请你指出上面展开图各部分与几何体的哪一部分相对应?
剪一剪、画一画:动手把一个立方体的包装盒沿一边剪开,铺平,看看它的展开图由哪些平面图形组成;再把展开的纸板复原,你有什么体会? 再将所有的展开图画出来,
以上画出了部分展开图,除此之外还有5种,共有11种, 请你画出其余5种。
活动2.探究立体图形的折叠
探究:下图是一些立体图形的展开图,用它们能围成怎样的立体图形?
凭想象回答,回答不出来的,就把它画在纸片上,剪下来折叠。
做一做:下面是一些常见几何体的展开图,你能正确说出这些几何体的名字么?
活动3.课堂练习
课本118页练习2
四.盘点提升
1.知道了什么?
2.学会了什么?
3.发现了什么?
五.达标检测
1.下列图形中,不是正方体的表面展开图的是( )(119页练习3题)
2. 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐 C.沾 D.益
反思:
课题 4.1.2点、线、面、体
课型:新课
学时:1学时
一.目标:
1.了解几何体、平面和曲面的意义,能正确判定围成几何体的面是平面还是曲面;
2.了解几何图形构成的基本元素是点、线、面、体及其关系,能正确判定由点、面、体经过运动变化形成的简单的几何图形;
3.判定围成立体图形的面是平面还是曲面,探索点、线、面、体之间的关系。
4.探索点、线、面、体运动变化后形成的图形。
预习
1.出示一个长方体模型,请同学们认真观察。
2.回答问题:这个长方体有几个面?面与面相交成了几条线?线与线相交成几个 点?
三.活动探究
1.经过学生的独立思考,然后在小组中进行交流,在小组讨论中,评价并修正自己的结论。(教师进行巡视,及时给予指导,教师对学生分布的答案作鼓励性评价)。
2.几何体的概念
(1)长方体是一个几何体,我们还学过哪些几何体?
____________________________________________________________;
(2)观察长方体和圆柱体,说出围成这两个几何体的面有哪些?这些面有什么区别?
3.面的分类
通过对上面问题的解决,得出面的分类:____面和___面。
面与面相交成线,线有___线和____线;线与线相交成_____;
4. 点、线、面、体
教师指导学生看课本第119-120页内容,观察图片能发现什么结论?
点、线、面、体的关系:点动成_____,线动成___________,面动成________。
请你再举出生活中的一些实例:
5.点、线、面、体与几何图形关系.
指导学生阅读课本第120页内容,总结出点、线、面、体与几何图形的关系
几何图形都是由_______________________组成的,________是构成图形的基本元素。
【课堂练习】
课本第120页练习1、2;
四.盘点提升
1.本节课我们主要学习了什么?
2. 本节课我们有哪些收获?
达标检测
1.人在雪地上走,他的脚印形成一条_______,这说明了______的数学原理;
2.体是由_______围成的,面和面相交形成_______,线和线相交形成______;
3.点动成________,线动成______,面动成_______;
4.将三角形绕直线L旋转一周,可以得到如下图所示立体图形的是------
课题 4.2直线、射线、线段(1)
课型:新课
学时:1学时
一.目标:
1.能在现实情境中,经历画图的数学活动过程,理解并掌握直线的性质,能用几何语言描述直线性质;
2.会用字母表示直线、射线、线段,会根据语言描述画出图形;
3.理解并掌握直线性质,会用字母表示图形和根据语言描述画出图形;
二、预习热身
1.在小学已经学过了直线、射线、线段.请你画出一条直线、一条射线、一条线段?
直线 射线 线段
2.填写下列表格:
端点个数
延伸方向
能否度量
线段
射线
直线
三、活动探究
活动1、探究直线的性质
(1)如果你想将一根细木条固定在墙上,至少需要几个钉子?操作一下,试试看。 答:
(2)经过一个已知点的直线,可以画多少条直线?请画图说明。
答: O ·
(3)经过两个已知点画直线,可以画多少条直线?请画图试试。
答:
猜想:如果将细木条抽象成直线,将钉子抽象为点,你可以得到什么结论?
1.直线的基本性质:
经过两点有 条直线,并且 条直线;
简述为:
举例说明直线的性质在日常生活中的应用:
(1) 在挂窗帘时,只要在两边钉两颗钉子扯上线即可,这是因为
(2)建筑工人在砌墙时拉参照线,木工师傅锯木板时,用墨盒弹墨线,都是根据
(3)你还能从生活中举出应用直线的基本性质的例子吗?试试看:
2、直线有两种表示方法:①用一个小写字母表示;②用两个大写字母表示。
平面上一个点与一条直线的位置有什么关系?
①点在直线上;②点在直线外。
当两条直线有一个共公点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
3、射线和线段的表示方法:
如图。显然,射线和线段都是直线的一部分。
图①中的线段记作线段AB或线段a;图②中的射线记作射线OA或射线m。
注意:用两个大写字母表示射线时,表示端点的字母一定要写在前面。
思考:直线、射线和线段有什么联系和区别?
(自己小结一下)
活动2.课堂练习
1.下列给线段取名正确的是 ( )
A.线段M B.线段m C.线段Mm D.线段mn
2.如图,若射线AB上有一点C,下列与射线AB是同一条射线的是 ( )
A.射线BA B.射线AC
C.射线BC D.射线CB
3.下列语句中正确的个数有 ( )
①直线MN与直线NM是同一条直线 ②射线AB与射线BA是同一条射线
③线段PQ与线段QP是同一条线段
④直线上一点把这条直线分成的两部分都是射线.
A.1个 B.2个 C.3个 D.4个
4.课本126页练习
四.盘点提升
通过本节课的学习你有什么收获?
五.达标检测
1.如图,线段AB上有两点C、D,则共有 条线段。
2.变形题:往返于甲、乙两地的客车中途要停靠三个车站,有多少种不同的票价?要准备多少种不同的车票?
教学反思:
课题 4.2直线、射线、线段(2)
课型:新课
学时:1学时
一.目标:
1、会用尺规画一条线段等于已知线段;
2、会比较两条线段的长短;
3、理解线段中点的概念,了解“两点之间,线段最短”的性质。
4.线段的中点概念,“两点之间,线段最短”的性质是重点;
5.画一条线段等于已知线段是难点。
二.预习热身
1、过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是对的。
三.活动探究
活动1自主学习
问题:现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:
已知线段a,画一条线段等于已知线段。
1.作一条线段等于已知线段
现在我们来解决这个问题。
作法:
(1)作射线AM
(2)在AM上截取AB= a。
则线段AB为所求。
应用:已知线段a、b,求作线段AB=a+b。
解:(1)作射线AM;
(2)在AM上顺次截取AC=a,CB= b。
则AB= a+b为所求。
做一做:作线段AB=a-b。
活动2.比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?
我们先来回答下面的问题。
怎样比较两个同学的身高?
一是用尺子测量;二是站在一起比(脚在同一高度)。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
(1)度量法:用刻度尺分别量出两条线段的长度从而进行比较。
(2)把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。(如图)
AB<CD AB>CD AB=CD
活动3.线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点;
记作AM=MB或AM=MB=1/2AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的三等分点。类似地,还有四等分点,等等。 请同学们思考课本131页的思考?
结论:两点所连的线中,
简单地说成:___________________________________
你能举出这条性质在生活中的一些应用吗?
两点间的距离的定义:___________________________________
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
【课堂练习】
1、课本128页练习1、2
四.盘点提升
1、画一条线段等于一条已知线段。
2、怎样比较两条线段的长短?
3、线段的性质是什么?
4、什么是两点间的距离?
五.达标检测
1、把弯曲的河道改直后,缩短了河道的长度,这是因为 ;
2、已知,如图,AB=16㎝,C是BC的中点,且AC=10㎝,D是AC的中点,E是BC的中点,求线段DE的长。
3.在直线上顺次取A、B、C三点,使 AB=4㎝,BC=3㎝,点O是线段AC的中点,则线段OB的长是〔 〕
A、2㎝ B、1.5㎝ C、0.5㎝ D、3.5㎝
4.已知线段AB=5㎝,C是直线AB上一点,若BC=2㎝,则线段AC的长为
课题 4.3.1角
课型:新课
学时:1学时
一、目标
1、理解角的概念,会适当表示角
2、认识角的度量单位:度、分、秒
3、会进行简单的换算和角度的计算
二、预习热身
1、观察课本132页图4.3.1;思考问题:
如图,时钟的时针与分针,棱锥相交的两条棱,直尺相交的两条边,给我们什么平面图形的形象?
2、角的定义1: 有__________________的两条射线组成的图形叫做角。
这个公共端点是角的________,这两条射线是角的__________。
3、 角的表示 ① ② ③ ④
4、用适当的方法表示下图中的每个角:
三、活动探究
活动1、
(1)演示:把一条射线由OA的位置绕点O旋转到OB的位置,如图(1),射线开始的位置OA与旋转后的位置OB组成了什么图形?
(2)角的定义2: 角也可以看作由一条射线绕着它的端点旋转面形成的。
如图(2),当射线旋转到起始位置OA与终止位置OB在一条直线上时,形成_____角;
如图(3),继续旋转,OB与OA重合时,又形成________角;
思考:平角是一条直线吗?周角是一条射线吗?为什么?
活动2、角的度量
(1)阅读课本133页;填空:
1周角=_____0 , 1平角=_____0;
10=____′, 1′=_____′′;
如∠a的度数是48度56分37秒,记作∠a=48056′37′′。
(2)度、分、秒是常用的角的度量单位,以度、分、秒为单位的角的度量制,叫做角度制。
注意:角的度、分、秒与时间的时、分、秒一样,都是60进制,计算时,借1当成60,满60进1。
例 计算:(1)53028′+47035′; (2)17027′+3050′;(学生自己完成)
活动3、讨论
1、8时30分,钟表中时针与分针的夹角为多少度?8时45分呢?
2、38015′和38.150相等吗?若不相等,哪个大?
四、盘点提升
你在本课中收获了什么?还有疑问吗?
五、达标检测
1、(37.2)0 = 度 分; 98030′= 度。
2、下午2时30分,钟表中时针与分针的夹角为〔 〕
A、900 B、1050 C、1200 D、1350
3、如图,A、B、C在一直线上,已知1=53°,2=37°;CD与CE垂直吗?
总结反思:
课题 4.3.2角的比较与运算
课型:新课
学时:1学时
一、目标呈现
1、会比较两个角的大小,能分析图中角的和差关系;
2、理解角平分线的概念,会画角平分线。
二、预习热身
1、怎样比较图中线段AB、BC、CA的长短?
方法:1. 方法2.
那么怎样比较∠A、 ∠ B、 ∠ C的大小呢?
三、活动探究
活动1 : 比较角的大小
(1)度量法:用量角器量出角的度数,然后比较它们的大小。
(2)叠合法:把两个角叠合在一起比较大小。
小组合作:
比较大小:∠AOB __ ∠AOB ∠AOB___ ∠AOB′ ∠AOB___ ∠AOB′
活动2:认识角的和差
思考:如图,图中共有几个角?它们之间有什么关系?
图中共有 个角:∠AOB、∠AOC、∠BOC。它们的关系是:
3、用三角板拼角
探究:借助三角尺画出150,750的角。
一副三角板的各个角分别是多少度?___________________________________
你还能画出哪些角?有什么规律吗?
还能画出___________________________________
规律是:凡是 的倍数的角都能画出。
活动3:角平分线
1、在一张纸上画出一个角并剪下,将这个角对折,使其两边重合.想想看,折痕与角两边所成的两个角的大小有什么关系?
如图(1)
角的平分线:从一个角的_____出发,把这个角分成_______的两个角的射线,叫做这个角的平分线。 类似地,还有角的三等分线等。如图(2)中的OB、OC。
OB是∠AOC的一平分线,可以记作:
∠AOC=2∠AOB=2∠BOC或∠AOB=∠BOC= 。
2、怎样画角平分线?
3、合作学习
例1 如图,O是直线AB上一点,∠AOC=53017′,求∠ BOC的度数。
例2 把一个周角7等分,每一份是多少度的角(精确到分)
四、盘点提升
你在本课中收获了什么?还有疑问吗?
五、达标检测
1、课本136页1、2、3(做在书上)
2、如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数。
总结反思
课题:4.3.3 余角和补角(1)
课型:新课
学时:1学时
一、目标呈现
1、能在具体的现实情境中,认识一个角的余角和补角;
2、会求一个角的余角和补角。
二、预习热身
在一副三角板中同一块三角板的两个锐角和等于多少度?
如图1,已知∠1=61°,∠2=29°,那么∠1+∠2= 。
如 图 2,已知点A、O、B在一直线上 ,∠COD=90°,那么∠1+∠2= 。
互为余角
(4)如图3,已知∠1=62°,∠2=118°,那么 ∠1+∠2=
(5)如图4,A、O、B在同一直线上,∠1+∠2=
互为补角
三、活动探究
活动1、(自主完成)
例1、若一个角的补角等于它的余角4倍,求这个角的度数。
例2:如图,∠AOC=∠COB=90°,∠DOE=90°,A、O、B三点在一直线上
(1)写出∠COE的余角,∠AOE的补角;
(2)找出图中一对相等的角,并说明理由;
活动2、(讨论完成)
1、一个角的余角比它的补角的还少,求这个角的度数。
2、若和互余,且:=7:2,求、的度数。
四、盘点提升: 你在本课中收获了什么?还有疑问吗?
五、达标检测
完成课本139页练习1、2、3;
总结反思
课题:4.3.3余角和补角(2)
课型:新课
学时:1学时
一、目标呈现
1、掌握余角和补角的性质。
2、了解方位角,能确定具体物体的方位。
二、预习热身
1.70°的余角是 ,补角是 ;
2.∠((∠( <90°)的它的余角是 ,它的补角是 ;
三、活动探究
活动1、 探究补角的性质:
例3、如图, ∠1与∠2互补,∠3与∠4互补, ∠1= ∠3,那么∠2与∠4相等吗?为什么?
分析:(1)∠1与∠2互补,∠2等于什么?∠2=1800 - ,
∠3与∠4互补,∠4等于什么? ∠4=1800 - 。
(2)当∠1= ∠3时,∠2与∠4有什么关系?为什么?
∠2=∠4(等量减等量,差相等)
上面的结论,用文字怎么叙述?
补角的性质:等角的 相等。
探究余角的性质:
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
余角性质:等角的 相等
活动2、方位角:
(1)认识方位:
正东、正南、正西、正北、东南、西南、西北、东北。
(2)找方位角:
例4:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线。
(师生共同完成)
活动3、完成练习
1.如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,
请说出∠1与∠3之间的关系?并试着说明理由?
2.在同一图上画出表示下列方向的射线。
(1)北偏西30°(2)东南方向 (3)被骗东15° (4)南偏西75°
四、盘点提升: 你在本课中收获了什么?还有疑问吗?
五、达标检测
1、和都是的补角,则 ;
2、如果,则的关系是 ,
理由是 ;
3、A看B的方向是北偏东21°,那么B看A的方向( )
A 南偏东69° B 南偏西69° C 南偏东21° D 南偏西21°
4、在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,
则∠AOB的度 数是( )
A 100° B 70° C 180° D 140°
5. 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,
请说出∠1与∠3之间的关系?并试着说明理由?
总结反思
课题: 第四章 图形认识初步复习(两课时)
课型:新课
学时:2学时
一、目标呈现
1.直观认识立体图形,掌握平面图形(线段、射线、直线)的基本知识;
2.掌握角的基本概念,能利用角的知识解决一些实际问题。
二、知识回顾
(一)几何图形的认识
1、下面是我们学习过的一些数学名词,你能用自己的语言简短地描述它们吗?
立体图形 平面图形 展开图
两点间的距离 余角 补角
2、与以前相比,你对直线、射线、线段和角有什么新的认识?
(二)直线的性质:
经过两点有一条直线,并且只有一条直线。即: __________确定一条直线。
(三)线段的性质和两点间的距离
1、线段的性质:两点之间,_______________。
2、两点间的距离:连接两点的_______________,叫做两点间的距离。
3、线段的中点及等分点的意义
若点C把线段AB分为________的两条线段AC和BC,则点C叫做线段的中点。
(四)角的概念
1、角的定义和表示
(1)有_______________的两条射线组成图形叫做角。这是从静止的角度来定义的。
由一条射线绕着_______________旋转而成的图形叫做角。这是从运动的角度来定义的。
(2)角的表示:
①用三个大写字母表示;②用一个大写字母表示;③用阿拉伯数字或希腊字母表示。
2、角的度量
10=60′;1′=60′′.
3、角的比较
比较角的方法:度量法和叠合法。
4、角的平分线
从一个角的顶点出发,把这个角分成________的两个角的射线,叫做这个角的平分线。
表示为
∠AOC= ∠COB
或∠ AOC=∠COB= 1/2∠AOB
或2∠ AOC=2∠COB= ∠AOB
5、余角和补角
(1)定义:如果两个角的和等于______,就说这两个角互为余角。
如果两个角的和等于______,就说这两个角互为补角。
注意:余角和补角是两个角之间的关系;只与数量有有关,而与位置无关。
(2)余角和补角的性质:
同角(等角)的余角相等。
同角(等角)的补角相等。
6、方位角
三、合作学习
1、 如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,画出从不同方向看到的平面图形。
2、(1)如图,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点,求线段MN的长;
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由。
(3)若C在线段AB的延长线上,且满足ACBC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由。
3、如图,∠AOB是直角, ∠ AOC=50°,ON是∠ AOC的平分线,OM是∠ BOC的平分线。
(1)求∠ MON的大小;
(2)当∠ AOC= 时, ∠ MON等于多少度?
(3)当锐角∠ AOC的大小发生改变时, ∠ MON的大小也会发生改变吗?为什么?
达标检测
一、选择题:
1、下列说法正确的是( )
A.射线AB与射线BA表示同一条射线。 B.连结两点的线段叫做两点之间的距离。
C.平角是一条直线。 D.若∠1+∠2=900,∠1+∠3=900,则∠2=∠3;
2、5点整时,时钟上时针与分钟 之间的夹角是〔 〕
A.210° B.30° C.150° D.60°
3、如图,射线OA表示〔 〕
A、南偏东700 B、北偏东300
C、南偏东300 D、北偏东700
4、下列图形不是正方体展开图的是〔 〕
5、若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则〔 〕
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠
二、填空题:
6、 38°41′的余角等于_____,123°59′的补角等于_____;
7、根据下列多面体的平面展开图,填写多面体的名称。
(1)__________,(2)__________,(3)_________。
8、互为余角的两个角之差为35°,则较大角的补角是_____;
9、 45°52′48″=_________度, 126.31°=____°____′____″;
25°18′÷3=__________;
10、如图,已知CB=4,DB=7,D是AC的中点,
则求AC的长度。
11、如图①直线l表示一条笔直的公路,在公路两旁有两上村庄A和B,要在公路边修建一个车站C,使车站C到村庄A和B的距离之和最小,请找出村庄C点的位置,并说明理由。
五.盘点提升
1.如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
(1)指出图中∠AOD的补角,∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
2、观察下列图形,并阅读图形下面的相关文字:
猜想:(1)5条直线最多有几个交点?6条直线呢?
(2)n条直线相交最多有几个 交点
第四章 图形认识初步 检测试卷(45分钟完成满分100分)
班级 姓名 成绩
一、填空题(每空4分,共40分)
1.圆柱的侧面展开图是 ;
2.已知与互余,且,则为 ;
3.如果一个角的补角是,那么这个角的余角是________;
4.乘火车从A站出发,沿途经过3个车站可到达B站,那么在AB两站之间最多共有________种不同的票价;
5.如图,若是中点,是中点,若,,_________。
6.要在墙上固定一根木条,至少要 个钉子,根据的原理是 。
7.________度________分; 8. ________;
9.小明每天下午5:30回家,这时分针与时针所成的角的度数为____度。
二、选择题(每题4分,共20分)
10.下列判断正确的是( )
A.平角是一条直线 B.凡是直角都相等
C.两个锐角的和一定是锐角 D.角的大小与两条边的长短有关
11.下列哪个角不能由一副三角板作出( )
A. B. C. D.
12.若,则∠α与∠β的关系是( )
A.互补 B.互余 C.和为钝角 D.和为周角
13.平面上A、B两点间的距离是指( )
A.经过A、B两点的直线 B. 射线AB
C. A、B两点间的线段 D. A、B两点间线段的长度
14.一个立体图形的三视图如图所示,那么它是 ( )
A.圆锥 B.圆柱 C.三棱锥 D.四棱锥
三、解答题:(共40分)
15.根据下列要求画图:(10分)
(1)连接线段AB;
(2)画射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一点D(点C、D不与点A重合),画直线CD,使直线CD与射线OB交于点E。
16、如图所示的几何体是由5个相同的正方体搭成的, 请画出它的主视图、左视图和俯视图(9分)
17.如图所示,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,若∠AOC=68°,则∠BOF和∠EOF是多少度?(9分)
18.(1)如下图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的的长度.
(2)在(1)中,如果AC=acm,,其它条件不变,你能猜出MN的长度吗?请你用 一句简洁的话表述你发现的规律.
(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M、N分别是AC、BC的中点,求MN的长度。”结果会有变化吗?如果有,求出结果。(12分)
课题 4.1.1认识几何图形(1)
课型:新课
学时:1学时
主备人:廖晓阳
审阅人:黄坤权 廖晓阳 周飞 费光锦 刘国芬 苏国庆 吴诗言
一.目标:
1、通过观察生活中的大量图片或实物,经历把实物抽象成几何图形的过程;
2、能由实物形状想象出几何图形,由几何图形想象出实物形状;
3、能识别一些简单几何体,正确区分平面图形与立体图形。
二预习热身
同学们,你仔细观察过我们生活的世界吗?从城市宏伟的建筑到乡村简朴的住宅,从四通八达的立交桥到街头巷尾的交通标志,从古老的剪纸艺术到现代化的城市雕塑,从自然界形态各异的动物到北京的申奥标志……,包含着形态各异的图形。图形的世界是丰富多彩的!那就让我们走进图象的世界去看看吧。
三.活动探究
活动1.(1)仔细观察图4.1-1,让同学们感受是丰富多彩的图形世界;
(2)出示一个长方体的纸盒,让同学们观察图4.1-2回答问题:
从整体上看,它的形状是什么?从不同侧面看,你看到了什么图形?只看棱、顶点等局部,你又看到了什么?
我们见过的长方形、圆柱、圆锥、球、圆、线段、点,以及小学学习过的三角形、四边形等,都是从形形色色的物体外形中得出的。我们把这些图形称为几何图形。
注意:当我们关注物体的形状、大小和位置时,得出了几何图形,它是数学研究的主要对象之一,而物体的颜色、重量、材料等则是其它学科所关注的。
活动2.
思考第115页思考题并出示实物(如茶叶、地球仪、字典及魔方等)及多媒体演示(如谷堆、帐篷、金字塔等),它们与我们学过的哪些图形相类似?
长方体、正方体、球、圆柱、圆锥等它们各部分不都在同一平面内,它们是立体图形。
想一想
生活中还有哪些物体的形状类似于这些立体图形呢?
思考:课本115页图4.1-4中实物的形状对应哪些立体图形?把相应的实物与图形用线连起来。
活动3.
平面图形的概念
线段、角、三角形、长方形、圆等它们的各部分都在同一平面内,它们是平面图形。
思考:课本116页图4.1-5的图中包含哪些简单的平面图形?
请再举出一些平面图形的例子。
长方形、圆、正方形、三角形、……。
思考:立体图形与平面图形是两类不同的几何图形,它们的区别在哪里?它们有什么联系?
立体图形的各部分不都在同一平面内,而平面图形的各部分都在同一平面内;
立体图形中某些部分是平面图形。
四、盘点提升
你在本课中收获了什么?还有疑问吗?
1、
2、平面图形与立体图形的关系:
立体图形的各部分不都在同一平面内,而平面图形的各部分都在同一平面内;
立体图形中某些部分是平面图形。
五、达标检测
1.下列几种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;⑥球.其中属于立体图形的是( )
A. ①②③; B. ③④⑤; C. ① ③⑤; D. ③④⑤⑥
2.课本116页练习
课题4.1.1几何图形(2)
课型:新课
学时:1学时
一.目标:
1.经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果,了解为什么要从不同方向看;
2.能画出从不同方向看一些基本几何体(直棱柱、圆柱、圆锥、球)以及它们的简单组合得到的平面图形;
3.识别一些基本几何体(直棱柱、圆柱、圆锥、球)以及它们的简单组合得到的平面图形
4.画出从正面、左面、上面看正方体及简单组合体的平面图形
二.引入
多媒体演示庐山景观,请学生背诵苏东坡《题西林壁》并说说诗中意境。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
从数学的角度来理解是什么意思呢?
三.活动探究
活动1
1.说一说:分别从正面、左面、上面观察乒乓球、粉笔盒、茶叶盒,各能得到什么平面图形?(出示实物)
2.画一画:长方体、圆锥分别从正面、左面、上面观察,各能得到什么图形?试着画一画.(出示实物)这样,我们将立体图形转化成了平面图形
活动2.
从正面、左面、上面观察得到的平面图形你能画出来吗?(117页图4.1-7)
小组合作学习,动手画一画,并进行展示
探究:分别从正面、左面、上面观察课本117页图4.1-8这个图形,分别画出得到的平面图形。
活动3.
【课堂练习】:
课本118页练习1、
四.盘点提升:
1.本节课我们主要学习了什么?
2. 本节课我们有哪些收获?
3.你还有什么没有解决的问题?
五.达标检测
1. 如图是由七个相同的小正方体堆成的物体,从上面看这个物体的图是( )
2.右图是由几个小立方块所搭几何体的俯视图,请画出这个几何体的主视图和左视图。
【总结反思】:
课题4.1.1几何图形(3)
课型:新课
学时:1学时
一.目标:
1.能直观认识立体图形和展开图,了解研究立体图形方法。
2.通过观察和动手操作,经历和体验平面图形和立体图形相互转换的过程,培养动手操作能力,初步建立空间观念,发展几何直觉。
3.了解基本几何体与其展开图之间的关系,体会一个立体按照不同方式展开可得到不同的平面展开图。
4.正确判断哪些平面图形可以折叠为立体图形;某个立体图形的展开图可以是哪些平面图形
二.预习热身
我们把一些像墨水瓶盒、粉笔盒这样的纸盒沿它的表面适当剪开,可以展平成平面图形。这样的平面图形叫做相应立体图形的展开图。
你知道长方体、圆柱、圆锥和三棱柱的展开图是什么样子的吗?想象一下。
三.活动探究
活动1.探究立体图形的展开图
1、试一试:在你想象的基础上,请将准备好的长方体、圆柱、圆锥和三棱柱的纸盒剪开展平,看看与下面的展开图一样吗?
圆柱 圆锥 三棱柱 长方体
思考:请你指出上面展开图各部分与几何体的哪一部分相对应?
剪一剪、画一画:动手把一个立方体的包装盒沿一边剪开,铺平,看看它的展开图由哪些平面图形组成;再把展开的纸板复原,你有什么体会? 再将所有的展开图画出来,
以上画出了部分展开图,除此之外还有5种,共有11种, 请你画出其余5种。
活动2.探究立体图形的折叠
探究:下图是一些立体图形的展开图,用它们能围成怎样的立体图形?
凭想象回答,回答不出来的,就把它画在纸片上,剪下来折叠。
做一做:下面是一些常见几何体的展开图,你能正确说出这些几何体的名字么?
活动3.课堂练习
课本118页练习2
四.盘点提升
1.知道了什么?
2.学会了什么?
3.发现了什么?
五.达标检测
1.下列图形中,不是正方体的表面展开图的是( )(119页练习3题)
2. 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐 C.沾 D.益
反思:
课题 4.1.2点、线、面、体
课型:新课
学时:1学时
一.目标:
1.了解几何体、平面和曲面的意义,能正确判定围成几何体的面是平面还是曲面;
2.了解几何图形构成的基本元素是点、线、面、体及其关系,能正确判定由点、面、体经过运动变化形成的简单的几何图形;
3.判定围成立体图形的面是平面还是曲面,探索点、线、面、体之间的关系。
4.探索点、线、面、体运动变化后形成的图形。
预习
1.出示一个长方体模型,请同学们认真观察。
2.回答问题:这个长方体有几个面?面与面相交成了几条线?线与线相交成几个 点?
三.活动探究
1.经过学生的独立思考,然后在小组中进行交流,在小组讨论中,评价并修正自己的结论。(教师进行巡视,及时给予指导,教师对学生分布的答案作鼓励性评价)。
2.几何体的概念
(1)长方体是一个几何体,我们还学过哪些几何体?
____________________________________________________________;
(2)观察长方体和圆柱体,说出围成这两个几何体的面有哪些?这些面有什么区别?
3.面的分类
通过对上面问题的解决,得出面的分类:____面和___面。
面与面相交成线,线有___线和____线;线与线相交成_____;
4. 点、线、面、体
教师指导学生看课本第119-120页内容,观察图片能发现什么结论?
点、线、面、体的关系:点动成_____,线动成___________,面动成________。
请你再举出生活中的一些实例:
5.点、线、面、体与几何图形关系.
指导学生阅读课本第120页内容,总结出点、线、面、体与几何图形的关系
几何图形都是由_______________________组成的,________是构成图形的基本元素。
【课堂练习】
课本第120页练习1、2;
四.盘点提升
1.本节课我们主要学习了什么?
2. 本节课我们有哪些收获?
达标检测
1.人在雪地上走,他的脚印形成一条_______,这说明了______的数学原理;
2.体是由_______围成的,面和面相交形成_______,线和线相交形成______;
3.点动成________,线动成______,面动成_______;
4.将三角形绕直线L旋转一周,可以得到如下图所示立体图形的是------
课题 4.2直线、射线、线段(1)
课型:新课
学时:1学时
一.目标:
1.能在现实情境中,经历画图的数学活动过程,理解并掌握直线的性质,能用几何语言描述直线性质;
2.会用字母表示直线、射线、线段,会根据语言描述画出图形;
3.理解并掌握直线性质,会用字母表示图形和根据语言描述画出图形;
二、预习热身
1.在小学已经学过了直线、射线、线段.请你画出一条直线、一条射线、一条线段?
直线 射线 线段
2.填写下列表格:
端点个数
延伸方向
能否度量
线段
射线
直线
三、活动探究
活动1、探究直线的性质
(1)如果你想将一根细木条固定在墙上,至少需要几个钉子?操作一下,试试看。 答:
(2)经过一个已知点的直线,可以画多少条直线?请画图说明。
答: O ·
(3)经过两个已知点画直线,可以画多少条直线?请画图试试。
答:
猜想:如果将细木条抽象成直线,将钉子抽象为点,你可以得到什么结论?
1.直线的基本性质:
经过两点有 条直线,并且 条直线;
简述为:
举例说明直线的性质在日常生活中的应用:
(1) 在挂窗帘时,只要在两边钉两颗钉子扯上线即可,这是因为
(2)建筑工人在砌墙时拉参照线,木工师傅锯木板时,用墨盒弹墨线,都是根据
(3)你还能从生活中举出应用直线的基本性质的例子吗?试试看:
2、直线有两种表示方法:①用一个小写字母表示;②用两个大写字母表示。
平面上一个点与一条直线的位置有什么关系?
①点在直线上;②点在直线外。
当两条直线有一个共公点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
3、射线和线段的表示方法:
如图。显然,射线和线段都是直线的一部分。
图①中的线段记作线段AB或线段a;图②中的射线记作射线OA或射线m。
注意:用两个大写字母表示射线时,表示端点的字母一定要写在前面。
思考:直线、射线和线段有什么联系和区别?
(自己小结一下)
活动2.课堂练习
1.下列给线段取名正确的是 ( )
A.线段M B.线段m C.线段Mm D.线段mn
2.如图,若射线AB上有一点C,下列与射线AB是同一条射线的是 ( )
A.射线BA B.射线AC
C.射线BC D.射线CB
3.下列语句中正确的个数有 ( )
①直线MN与直线NM是同一条直线 ②射线AB与射线BA是同一条射线
③线段PQ与线段QP是同一条线段
④直线上一点把这条直线分成的两部分都是射线.
A.1个 B.2个 C.3个 D.4个
4.课本126页练习
四.盘点提升
通过本节课的学习你有什么收获?
五.达标检测
1.如图,线段AB上有两点C、D,则共有 条线段。
2.变形题:往返于甲、乙两地的客车中途要停靠三个车站,有多少种不同的票价?要准备多少种不同的车票?
教学反思:
课题 4.2直线、射线、线段(2)
课型:新课
学时:1学时
一.目标:
1、会用尺规画一条线段等于已知线段;
2、会比较两条线段的长短;
3、理解线段中点的概念,了解“两点之间,线段最短”的性质。
4.线段的中点概念,“两点之间,线段最短”的性质是重点;
5.画一条线段等于已知线段是难点。
二.预习热身
1、过A、B、C三点作直线,小明说有三条,小颖说有一条,小林说不是一条就是三条,你认为 的说法是对的。
三.活动探究
活动1自主学习
问题:现有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根木棒的长?
上面的实际问题可以转化为下面的数学问题:
已知线段a,画一条线段等于已知线段。
1.作一条线段等于已知线段
现在我们来解决这个问题。
作法:
(1)作射线AM
(2)在AM上截取AB= a。
则线段AB为所求。
应用:已知线段a、b,求作线段AB=a+b。
解:(1)作射线AM;
(2)在AM上顺次截取AC=a,CB= b。
则AB= a+b为所求。
做一做:作线段AB=a-b。
活动2.比较两条线段的长短
两条线段可能相等,也可能不相等,那么怎样比较两条线段的长短呢?
我们先来回答下面的问题。
怎样比较两个同学的身高?
一是用尺子测量;二是站在一起比(脚在同一高度)。
如果把两个同学看成两条线段,那么比较两条线段就有两种方法。
(1)度量法:用刻度尺分别量出两条线段的长度从而进行比较。
(2)把一条线段移到另一条线段上,使一端对齐,从而进行比较,我们称为叠合法。(如图)
AB<CD AB>CD AB=CD
活动3.线段的中点及等分点
如图(1),点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点;
记作AM=MB或AM=MB=1/2AB或2AM=2MB=AB。
如图(2),点M、N把线段AB分成相等的三段AM、MN、NB,点M、N叫做线段AB的三等分点。类似地,还有四等分点,等等。 请同学们思考课本131页的思考?
结论:两点所连的线中,
简单地说成:___________________________________
你能举出这条性质在生活中的一些应用吗?
两点间的距离的定义:___________________________________
注意:距离是用“数”来度量的,它是线段的长度,而不是线段本身。
【课堂练习】
1、课本128页练习1、2
四.盘点提升
1、画一条线段等于一条已知线段。
2、怎样比较两条线段的长短?
3、线段的性质是什么?
4、什么是两点间的距离?
五.达标检测
1、把弯曲的河道改直后,缩短了河道的长度,这是因为 ;
2、已知,如图,AB=16㎝,C是BC的中点,且AC=10㎝,D是AC的中点,E是BC的中点,求线段DE的长。
3.在直线上顺次取A、B、C三点,使 AB=4㎝,BC=3㎝,点O是线段AC的中点,则线段OB的长是〔 〕
A、2㎝ B、1.5㎝ C、0.5㎝ D、3.5㎝
4.已知线段AB=5㎝,C是直线AB上一点,若BC=2㎝,则线段AC的长为
课题 4.3.1角
课型:新课
学时:1学时
一、目标
1、理解角的概念,会适当表示角
2、认识角的度量单位:度、分、秒
3、会进行简单的换算和角度的计算
二、预习热身
1、观察课本132页图4.3.1;思考问题:
如图,时钟的时针与分针,棱锥相交的两条棱,直尺相交的两条边,给我们什么平面图形的形象?
2、角的定义1: 有__________________的两条射线组成的图形叫做角。
这个公共端点是角的________,这两条射线是角的__________。
3、 角的表示 ① ② ③ ④
4、用适当的方法表示下图中的每个角:
三、活动探究
活动1、
(1)演示:把一条射线由OA的位置绕点O旋转到OB的位置,如图(1),射线开始的位置OA与旋转后的位置OB组成了什么图形?
(2)角的定义2: 角也可以看作由一条射线绕着它的端点旋转面形成的。
如图(2),当射线旋转到起始位置OA与终止位置OB在一条直线上时,形成_____角;
如图(3),继续旋转,OB与OA重合时,又形成________角;
思考:平角是一条直线吗?周角是一条射线吗?为什么?
活动2、角的度量
(1)阅读课本133页;填空:
1周角=_____0 , 1平角=_____0;
10=____′, 1′=_____′′;
如∠a的度数是48度56分37秒,记作∠a=48056′37′′。
(2)度、分、秒是常用的角的度量单位,以度、分、秒为单位的角的度量制,叫做角度制。
注意:角的度、分、秒与时间的时、分、秒一样,都是60进制,计算时,借1当成60,满60进1。
例 计算:(1)53028′+47035′; (2)17027′+3050′;(学生自己完成)
活动3、讨论
1、8时30分,钟表中时针与分针的夹角为多少度?8时45分呢?
2、38015′和38.150相等吗?若不相等,哪个大?
四、盘点提升
你在本课中收获了什么?还有疑问吗?
五、达标检测
1、(37.2)0 = 度 分; 98030′= 度。
2、下午2时30分,钟表中时针与分针的夹角为〔 〕
A、900 B、1050 C、1200 D、1350
3、如图,A、B、C在一直线上,已知1=53°,2=37°;CD与CE垂直吗?
总结反思:
课题 4.3.2角的比较与运算
课型:新课
学时:1学时
一、目标呈现
1、会比较两个角的大小,能分析图中角的和差关系;
2、理解角平分线的概念,会画角平分线。
二、预习热身
1、怎样比较图中线段AB、BC、CA的长短?
方法:1. 方法2.
那么怎样比较∠A、 ∠ B、 ∠ C的大小呢?
三、活动探究
活动1 : 比较角的大小
(1)度量法:用量角器量出角的度数,然后比较它们的大小。
(2)叠合法:把两个角叠合在一起比较大小。
小组合作:
比较大小:∠AOB __ ∠AOB ∠AOB___ ∠AOB′ ∠AOB___ ∠AOB′
活动2:认识角的和差
思考:如图,图中共有几个角?它们之间有什么关系?
图中共有 个角:∠AOB、∠AOC、∠BOC。它们的关系是:
3、用三角板拼角
探究:借助三角尺画出150,750的角。
一副三角板的各个角分别是多少度?___________________________________
你还能画出哪些角?有什么规律吗?
还能画出___________________________________
规律是:凡是 的倍数的角都能画出。
活动3:角平分线
1、在一张纸上画出一个角并剪下,将这个角对折,使其两边重合.想想看,折痕与角两边所成的两个角的大小有什么关系?
如图(1)
角的平分线:从一个角的_____出发,把这个角分成_______的两个角的射线,叫做这个角的平分线。 类似地,还有角的三等分线等。如图(2)中的OB、OC。
OB是∠AOC的一平分线,可以记作:
∠AOC=2∠AOB=2∠BOC或∠AOB=∠BOC= 。
2、怎样画角平分线?
3、合作学习
例1 如图,O是直线AB上一点,∠AOC=53017′,求∠ BOC的度数。
例2 把一个周角7等分,每一份是多少度的角(精确到分)
四、盘点提升
你在本课中收获了什么?还有疑问吗?
五、达标检测
1、课本136页1、2、3(做在书上)
2、如图,O为直线AB上一点,射线OD、OE分别平分∠AOC、∠BOC,求∠DOE的度数。
总结反思
课题:4.3.3 余角和补角(1)
课型:新课
学时:1学时
一、目标呈现
1、能在具体的现实情境中,认识一个角的余角和补角;
2、会求一个角的余角和补角。
二、预习热身
在一副三角板中同一块三角板的两个锐角和等于多少度?
如图1,已知∠1=61°,∠2=29°,那么∠1+∠2= 。
如 图 2,已知点A、O、B在一直线上 ,∠COD=90°,那么∠1+∠2= 。
互为余角
(4)如图3,已知∠1=62°,∠2=118°,那么 ∠1+∠2=
(5)如图4,A、O、B在同一直线上,∠1+∠2=
互为补角
三、活动探究
活动1、(自主完成)
例1、若一个角的补角等于它的余角4倍,求这个角的度数。
例2:如图,∠AOC=∠COB=90°,∠DOE=90°,A、O、B三点在一直线上
(1)写出∠COE的余角,∠AOE的补角;
(2)找出图中一对相等的角,并说明理由;
活动2、(讨论完成)
1、一个角的余角比它的补角的还少,求这个角的度数。
2、若和互余,且:=7:2,求、的度数。
四、盘点提升: 你在本课中收获了什么?还有疑问吗?
五、达标检测
完成课本139页练习1、2、3;
总结反思
课题:4.3.3余角和补角(2)
课型:新课
学时:1学时
一、目标呈现
1、掌握余角和补角的性质。
2、了解方位角,能确定具体物体的方位。
二、预习热身
1.70°的余角是 ,补角是 ;
2.∠((∠( <90°)的它的余角是 ,它的补角是 ;
三、活动探究
活动1、 探究补角的性质:
例3、如图, ∠1与∠2互补,∠3与∠4互补, ∠1= ∠3,那么∠2与∠4相等吗?为什么?
分析:(1)∠1与∠2互补,∠2等于什么?∠2=1800 - ,
∠3与∠4互补,∠4等于什么? ∠4=1800 - 。
(2)当∠1= ∠3时,∠2与∠4有什么关系?为什么?
∠2=∠4(等量减等量,差相等)
上面的结论,用文字怎么叙述?
补角的性质:等角的 相等。
探究余角的性质:
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
余角性质:等角的 相等
活动2、方位角:
(1)认识方位:
正东、正南、正西、正北、东南、西南、西北、东北。
(2)找方位角:
例4:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线。
(师生共同完成)
活动3、完成练习
1.如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,
请说出∠1与∠3之间的关系?并试着说明理由?
2.在同一图上画出表示下列方向的射线。
(1)北偏西30°(2)东南方向 (3)被骗东15° (4)南偏西75°
四、盘点提升: 你在本课中收获了什么?还有疑问吗?
五、达标检测
1、和都是的补角,则 ;
2、如果,则的关系是 ,
理由是 ;
3、A看B的方向是北偏东21°,那么B看A的方向( )
A 南偏东69° B 南偏西69° C 南偏东21° D 南偏西21°
4、在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,
则∠AOB的度 数是( )
A 100° B 70° C 180° D 140°
5. 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,
请说出∠1与∠3之间的关系?并试着说明理由?
总结反思
课题: 第四章 图形认识初步复习(两课时)
课型:新课
学时:2学时
一、目标呈现
1.直观认识立体图形,掌握平面图形(线段、射线、直线)的基本知识;
2.掌握角的基本概念,能利用角的知识解决一些实际问题。
二、知识回顾
(一)几何图形的认识
1、下面是我们学习过的一些数学名词,你能用自己的语言简短地描述它们吗?
立体图形 平面图形 展开图
两点间的距离 余角 补角
2、与以前相比,你对直线、射线、线段和角有什么新的认识?
(二)直线的性质:
经过两点有一条直线,并且只有一条直线。即: __________确定一条直线。
(三)线段的性质和两点间的距离
1、线段的性质:两点之间,_______________。
2、两点间的距离:连接两点的_______________,叫做两点间的距离。
3、线段的中点及等分点的意义
若点C把线段AB分为________的两条线段AC和BC,则点C叫做线段的中点。
(四)角的概念
1、角的定义和表示
(1)有_______________的两条射线组成图形叫做角。这是从静止的角度来定义的。
由一条射线绕着_______________旋转而成的图形叫做角。这是从运动的角度来定义的。
(2)角的表示:
①用三个大写字母表示;②用一个大写字母表示;③用阿拉伯数字或希腊字母表示。
2、角的度量
10=60′;1′=60′′.
3、角的比较
比较角的方法:度量法和叠合法。
4、角的平分线
从一个角的顶点出发,把这个角分成________的两个角的射线,叫做这个角的平分线。
表示为
∠AOC= ∠COB
或∠ AOC=∠COB= 1/2∠AOB
或2∠ AOC=2∠COB= ∠AOB
5、余角和补角
(1)定义:如果两个角的和等于______,就说这两个角互为余角。
如果两个角的和等于______,就说这两个角互为补角。
注意:余角和补角是两个角之间的关系;只与数量有有关,而与位置无关。
(2)余角和补角的性质:
同角(等角)的余角相等。
同角(等角)的补角相等。
6、方位角
三、合作学习
1、 如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,画出从不同方向看到的平面图形。
2、(1)如图,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点,求线段MN的长;
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由。
(3)若C在线段AB的延长线上,且满足ACBC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由。
3、如图,∠AOB是直角, ∠ AOC=50°,ON是∠ AOC的平分线,OM是∠ BOC的平分线。
(1)求∠ MON的大小;
(2)当∠ AOC= 时, ∠ MON等于多少度?
(3)当锐角∠ AOC的大小发生改变时, ∠ MON的大小也会发生改变吗?为什么?
达标检测
一、选择题:
1、下列说法正确的是( )
A.射线AB与射线BA表示同一条射线。 B.连结两点的线段叫做两点之间的距离。
C.平角是一条直线。 D.若∠1+∠2=900,∠1+∠3=900,则∠2=∠3;
2、5点整时,时钟上时针与分钟 之间的夹角是〔 〕
A.210° B.30° C.150° D.60°
3、如图,射线OA表示〔 〕
A、南偏东700 B、北偏东300
C、南偏东300 D、北偏东700
4、下列图形不是正方体展开图的是〔 〕
5、若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则〔 〕
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠
二、填空题:
6、 38°41′的余角等于_____,123°59′的补角等于_____;
7、根据下列多面体的平面展开图,填写多面体的名称。
(1)__________,(2)__________,(3)_________。
8、互为余角的两个角之差为35°,则较大角的补角是_____;
9、 45°52′48″=_________度, 126.31°=____°____′____″;
25°18′÷3=__________;
10、如图,已知CB=4,DB=7,D是AC的中点,
则求AC的长度。
11、如图①直线l表示一条笔直的公路,在公路两旁有两上村庄A和B,要在公路边修建一个车站C,使车站C到村庄A和B的距离之和最小,请找出村庄C点的位置,并说明理由。
五.盘点提升
1.如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
(1)指出图中∠AOD的补角,∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
2、观察下列图形,并阅读图形下面的相关文字:
猜想:(1)5条直线最多有几个交点?6条直线呢?
(2)n条直线相交最多有几个 交点
第四章 图形认识初步 检测试卷(45分钟完成满分100分)
班级 姓名 成绩
一、填空题(每空4分,共40分)
1.圆柱的侧面展开图是 ;
2.已知与互余,且,则为 ;
3.如果一个角的补角是,那么这个角的余角是________;
4.乘火车从A站出发,沿途经过3个车站可到达B站,那么在AB两站之间最多共有________种不同的票价;
5.如图,若是中点,是中点,若,,_________。
6.要在墙上固定一根木条,至少要 个钉子,根据的原理是 。
7.________度________分; 8. ________;
9.小明每天下午5:30回家,这时分针与时针所成的角的度数为____度。
二、选择题(每题4分,共20分)
10.下列判断正确的是( )
A.平角是一条直线 B.凡是直角都相等
C.两个锐角的和一定是锐角 D.角的大小与两条边的长短有关
11.下列哪个角不能由一副三角板作出( )
A. B. C. D.
12.若,则∠α与∠β的关系是( )
A.互补 B.互余 C.和为钝角 D.和为周角
13.平面上A、B两点间的距离是指( )
A.经过A、B两点的直线 B. 射线AB
C. A、B两点间的线段 D. A、B两点间线段的长度
14.一个立体图形的三视图如图所示,那么它是 ( )
A.圆锥 B.圆柱 C.三棱锥 D.四棱锥
三、解答题:(共40分)
15.根据下列要求画图:(10分)
(1)连接线段AB;
(2)画射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一点D(点C、D不与点A重合),画直线CD,使直线CD与射线OB交于点E。
16、如图所示的几何体是由5个相同的正方体搭成的, 请画出它的主视图、左视图和俯视图(9分)
17.如图所示,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,若∠AOC=68°,则∠BOF和∠EOF是多少度?(9分)
18.(1)如下图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的的长度.
(2)在(1)中,如果AC=acm,,其它条件不变,你能猜出MN的长度吗?请你用 一句简洁的话表述你发现的规律.
(3)对于(1)题,如果我们这样叙述它:“已知线段AC=6cm,BC=4cm,点C在直线AB上,点M、N分别是AC、BC的中点,求MN的长度。”结果会有变化吗?如果有,求出结果。(12分)
