青岛版八年级数学下册7.2勾股定理课件(共34张PPT)
文档属性
| 名称 | 青岛版八年级数学下册7.2勾股定理课件(共34张PPT) | 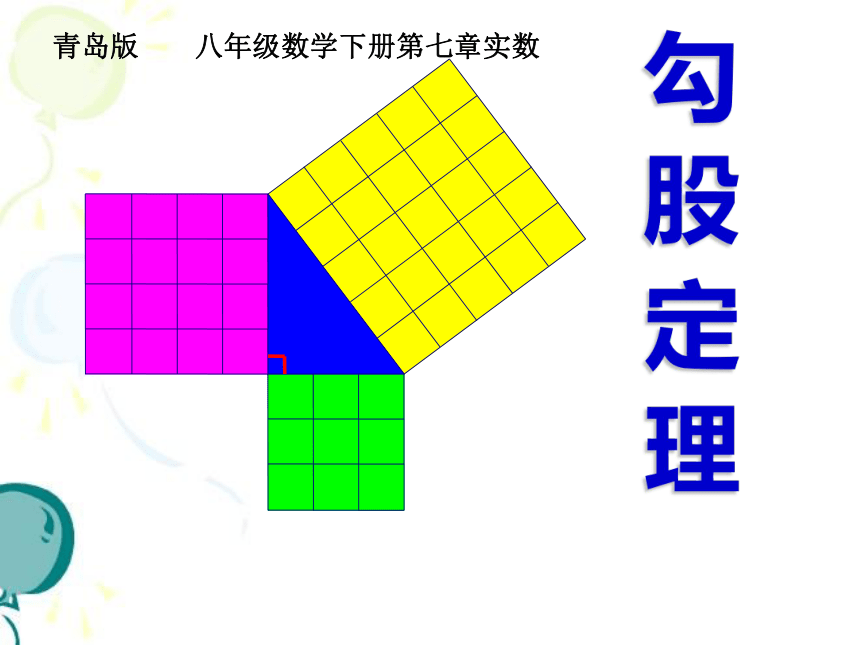 | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 15:49:19 | ||
图片预览





文档简介
(共34张PPT)
勾 股 定 理
青岛版 八年级数学下册第七章实数
情景导航
北京欢迎您!
学习目标:
1、经历勾股定理的探索过程,感受数形结合的思想,积
累数学活动的经验。
2、掌握勾股定理,会用勾股定理解决与直角三角形有
关 的问题。
3、尝试用多种方法验证勾股定理,体验解决问题策略
的多样化,发展推理能力。
重难点:
利用图形面积验证勾股定理
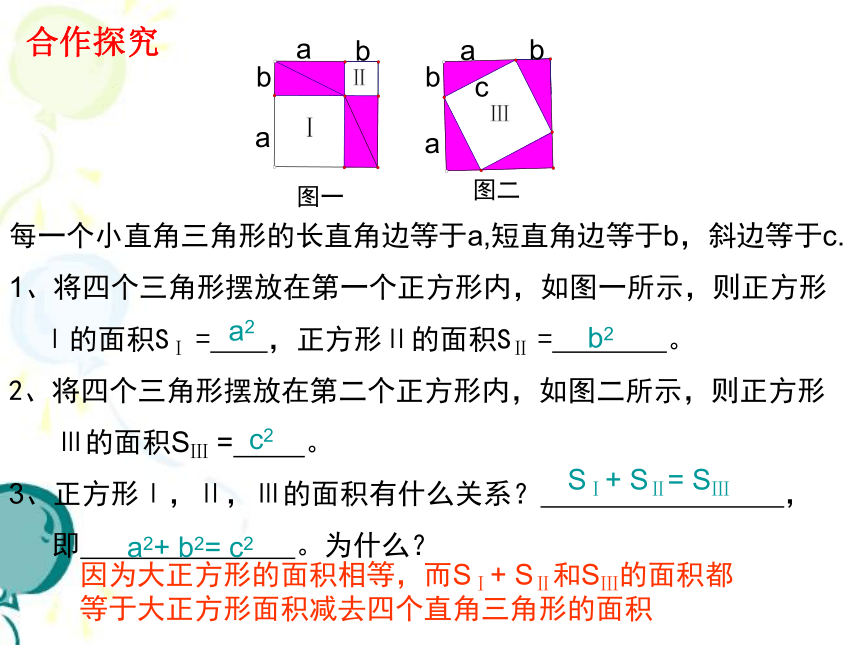
每一个小直角三角形的长直角边等于a,短直角边等于b,斜边等于c.
1、将四个三角形摆放在第一个正方形内,如图一所示,则正方形
Ⅰ的面积SⅠ = ,正方形Ⅱ的面积SⅡ = 。
2、将四个三角形摆放在第二个正方形内,如图二所示,则正方形
Ⅲ的面积SⅢ = 。
3、正方形Ⅰ,Ⅱ,Ⅲ的面积有什么关系? ,
即 。为什么?
。
a2
b2
c2
SⅠ+ SⅡ= SⅢ
a2+ b2= c2
因为大正方形的面积相等,而SⅠ+ SⅡ和SⅢ的面积都等于大正方形面积减去四个直角三角形的面积
图一
图二
合作探究
B
A
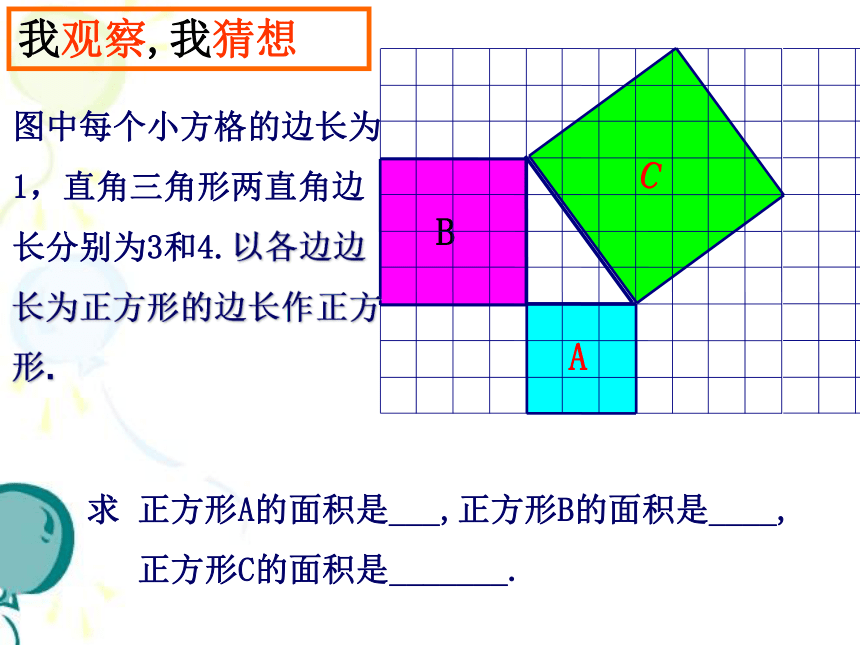
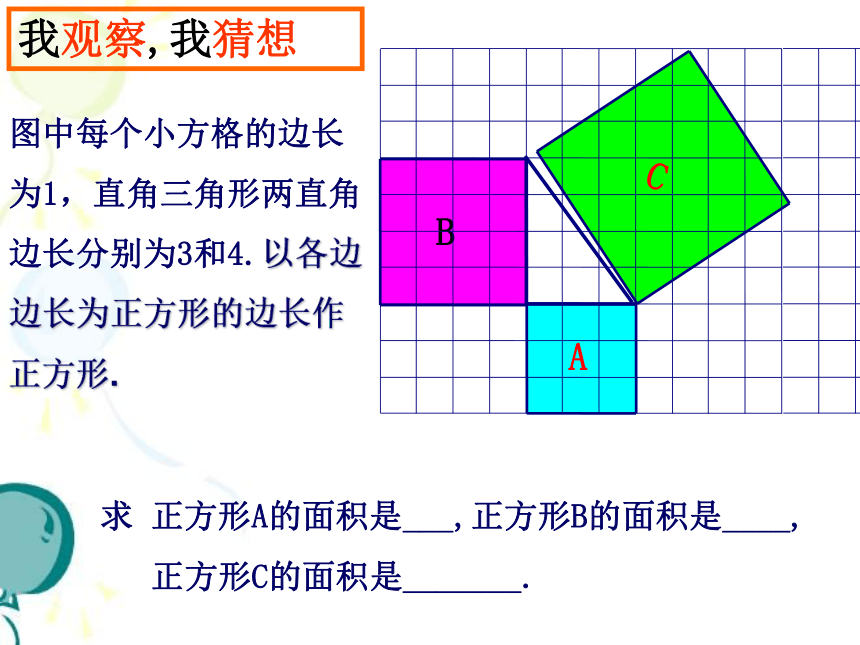
图中每个小方格的边长为 1,直角三角形两直角边长分别
为 3 和 4 .分别以直角三角形各边长向外作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
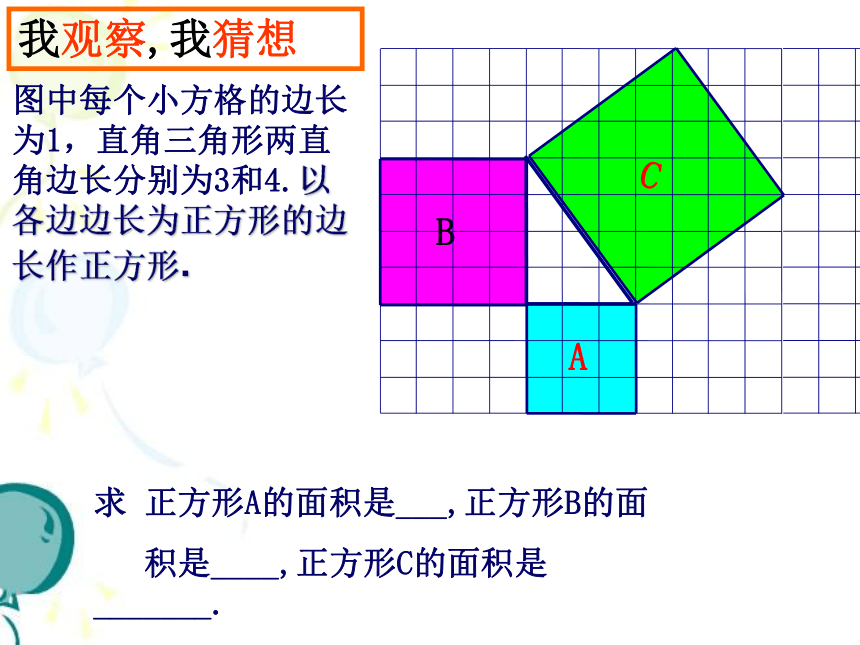
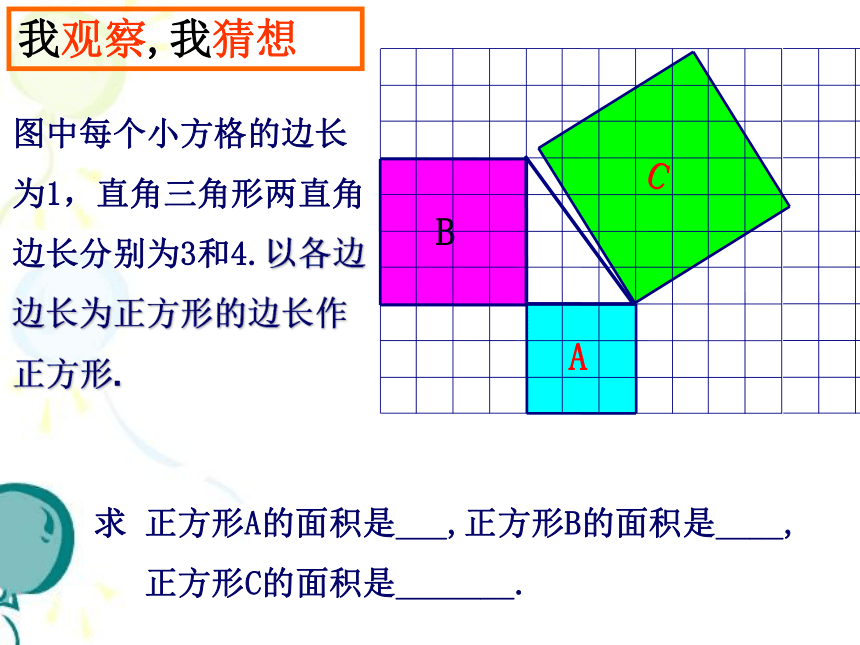
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
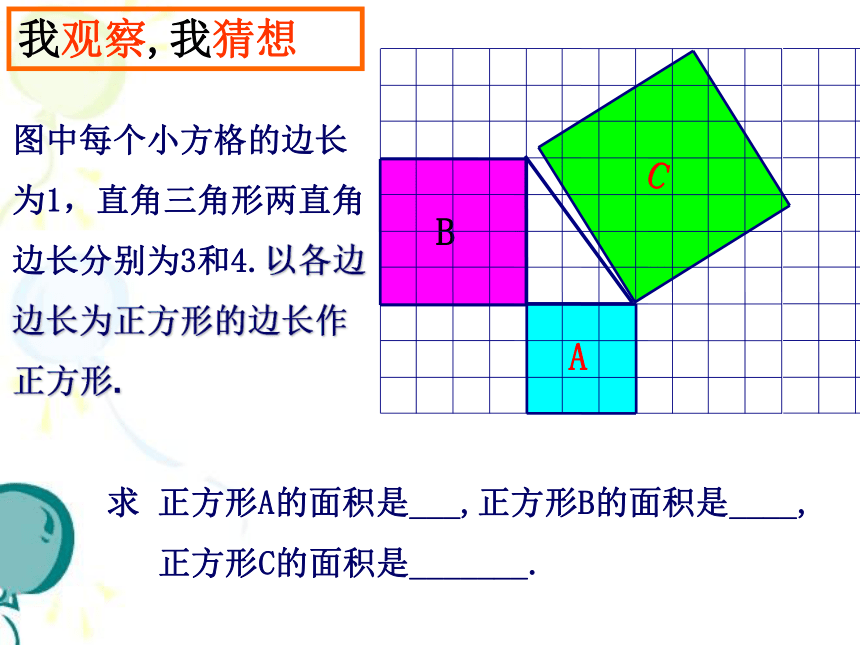
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面
积是____,正方形C的面积是_______.
我观察,我猜想
C
B
A
C
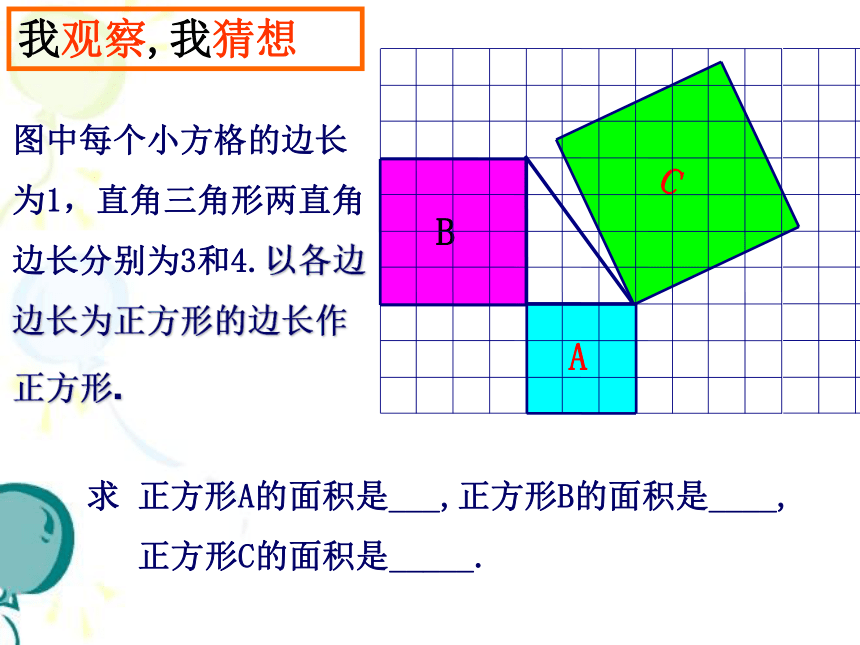
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_____.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求正方形A的面积是___,正方形B的面积是____,正方形C的面积是_______.
我观察,我猜想
C
B
A
C
a
c
b
SA+SB=SC
观察所得到的数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
我观察,我猜想
3
4
5
32+42=52
命题:如果直角三角形的两直角边长分
别为a、b,斜边长为c,那么
a2+b2=c2.
我实践,我验证
a
b
c
方法一
a
b
c
a
b
c
a
b
c
b
a
c
我实践,我验证
因为:S大正方形=(a+b)2
方法二
a
a
b
b
c
c
我实践,我验证
S梯形= (a+b)(a+b)
1
2
S梯形= (a+b)(a+b)
1
2
勾
股
定
理
:
如果直角三角形两直角边为a、b
斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和
等于斜边的平方。
我国古代把
直角三角形
中较短的直
角边称为勾,
较长的直角
边称为股,
斜边称为弦。
勾
股
弦
我总结,我获得
勾股定理
直角三角形中,两直角边的平方和等于斜边平方.
用数学式子表示:a2+b2=c2
a 勾
股
c 弦
b
⑵ a2 = c2 - b2
⑶ b2 = c2- a2
⑴ c2 = a2 + b2
勾股定理 直角三角形两直角边的平方和等于斜边的平方
请说出下列直角三角形中三边之间的关系。
(3)
我会用,我挑战
(1)
c
b
a
x
z
(2)
x
d
s
f
比一比看看谁算得快!
1.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
12
5
x
我会用,我挑战
8
x
17
A.8 米 B.9 米 C.10米 D.14米
2.一个长8 米,宽6 米的矩形草地,需在相对角的顶点间加一条小路,则小路的长为 ( )
8m
6m
别踩我,我怕疼!
我会用,我挑战
3、某楼房三楼失火,消防队员赶来救火,楼梯已被火封住上不去,了解到着火点距地面10米。消防队员取来9米长的云梯,已知梯子的底部到墙基的水平距离为4米,到地面的高度为2米,问消防队员能否进入三楼灭火?
学以致用
C
A
B
E
D
4
2
8
10
拓展延伸
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处,要爬行的最短路程(∏取3)是多少?
A
B
查阅有关勾股定理的历史资料,关注 验证勾股定理的其它证明方法方法.
勾股世界
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五.即“勾三、股四、弦五”.它被记载于我国古代著名的数学著作《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.
在西方,相传二千多年前,古希腊数学家毕达哥拉斯发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理.毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”.
毕达哥拉斯(Pythagoras 公元前582年一前497年 )是古希腊数学家,比商高晚出生五百多年。
请欣赏
美丽的勾股树
勾 股 定 理
青岛版 八年级数学下册第七章实数
情景导航
北京欢迎您!
学习目标:
1、经历勾股定理的探索过程,感受数形结合的思想,积
累数学活动的经验。
2、掌握勾股定理,会用勾股定理解决与直角三角形有
关 的问题。
3、尝试用多种方法验证勾股定理,体验解决问题策略
的多样化,发展推理能力。
重难点:
利用图形面积验证勾股定理
每一个小直角三角形的长直角边等于a,短直角边等于b,斜边等于c.
1、将四个三角形摆放在第一个正方形内,如图一所示,则正方形
Ⅰ的面积SⅠ = ,正方形Ⅱ的面积SⅡ = 。
2、将四个三角形摆放在第二个正方形内,如图二所示,则正方形
Ⅲ的面积SⅢ = 。
3、正方形Ⅰ,Ⅱ,Ⅲ的面积有什么关系? ,
即 。为什么?
。
a2
b2
c2
SⅠ+ SⅡ= SⅢ
a2+ b2= c2
因为大正方形的面积相等,而SⅠ+ SⅡ和SⅢ的面积都等于大正方形面积减去四个直角三角形的面积
图一
图二
合作探究
B
A
图中每个小方格的边长为 1,直角三角形两直角边长分别
为 3 和 4 .分别以直角三角形各边长向外作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面
积是____,正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_____.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
B
A
C
求 正方形A的面积是___,正方形B的面积是____,
正方形C的面积是_______.
我观察,我猜想
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
B
A
C
图中每个小方格的边长为1,直角三角形两直角边长分别为3和4.以各边边长为正方形的边长作正方形.
求正方形A的面积是___,正方形B的面积是____,正方形C的面积是_______.
我观察,我猜想
C
B
A
C
a
c
b
SA+SB=SC
观察所得到的数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
我观察,我猜想
3
4
5
32+42=52
命题:如果直角三角形的两直角边长分
别为a、b,斜边长为c,那么
a2+b2=c2.
我实践,我验证
a
b
c
方法一
a
b
c
a
b
c
a
b
c
b
a
c
我实践,我验证
因为:S大正方形=(a+b)2
方法二
a
a
b
b
c
c
我实践,我验证
S梯形= (a+b)(a+b)
1
2
S梯形= (a+b)(a+b)
1
2
勾
股
定
理
:
如果直角三角形两直角边为a、b
斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和
等于斜边的平方。
我国古代把
直角三角形
中较短的直
角边称为勾,
较长的直角
边称为股,
斜边称为弦。
勾
股
弦
我总结,我获得
勾股定理
直角三角形中,两直角边的平方和等于斜边平方.
用数学式子表示:a2+b2=c2
a 勾
股
c 弦
b
⑵ a2 = c2 - b2
⑶ b2 = c2- a2
⑴ c2 = a2 + b2
勾股定理 直角三角形两直角边的平方和等于斜边的平方
请说出下列直角三角形中三边之间的关系。
(3)
我会用,我挑战
(1)
c
b
a
x
z
(2)
x
d
s
f
比一比看看谁算得快!
1.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
12
5
x
我会用,我挑战
8
x
17
A.8 米 B.9 米 C.10米 D.14米
2.一个长8 米,宽6 米的矩形草地,需在相对角的顶点间加一条小路,则小路的长为 ( )
8m
6m
别踩我,我怕疼!
我会用,我挑战
3、某楼房三楼失火,消防队员赶来救火,楼梯已被火封住上不去,了解到着火点距地面10米。消防队员取来9米长的云梯,已知梯子的底部到墙基的水平距离为4米,到地面的高度为2米,问消防队员能否进入三楼灭火?
学以致用
C
A
B
E
D
4
2
8
10
拓展延伸
如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处,要爬行的最短路程(∏取3)是多少?
A
B
查阅有关勾股定理的历史资料,关注 验证勾股定理的其它证明方法方法.
勾股世界
我国是最早了解勾股定理的国家之一.早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五.即“勾三、股四、弦五”.它被记载于我国古代著名的数学著作《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.
在西方,相传二千多年前,古希腊数学家毕达哥拉斯发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理.毕达哥拉斯发现了勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”.
毕达哥拉斯(Pythagoras 公元前582年一前497年 )是古希腊数学家,比商高晚出生五百多年。
请欣赏
美丽的勾股树
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
