青岛版八年级数学下册6.4 三角形中位线定理课件(共18张PPT)
文档属性
| 名称 | 青岛版八年级数学下册6.4 三角形中位线定理课件(共18张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 537.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 16:17:43 | ||
图片预览




文档简介
(共18张PPT)
A
B
C
D
E
A
。B
C 。
D 。
。
E
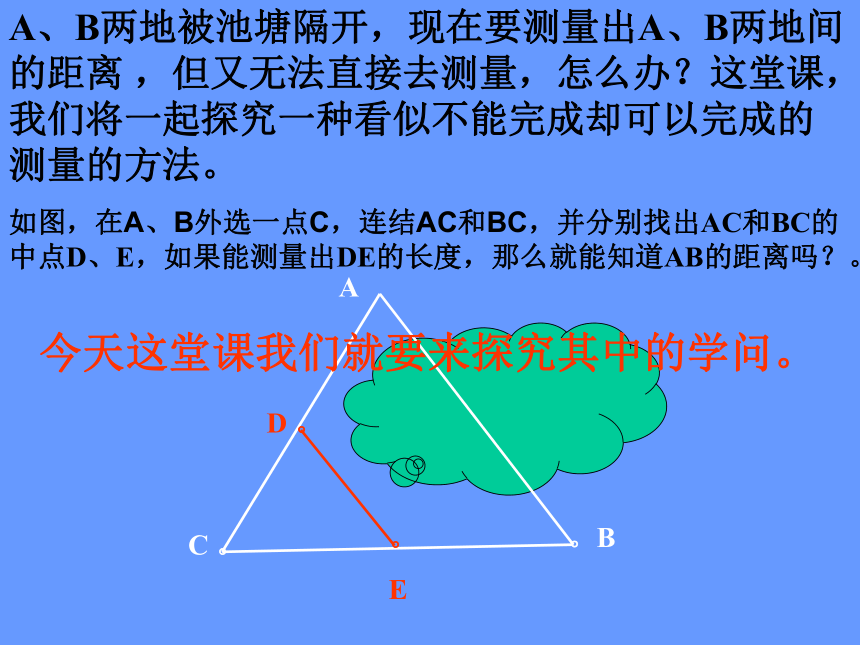
A、B两地被池塘隔开,现在要测量出A、B两地间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将一起探究一种看似不能完成却可以完成的测量的方法。
如图,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,那么就能知道AB的距离吗?。
今天这堂课我们就要来探究其中的学问。
补充:(1)平行线等分线段定理推论
经过三角形一边的中点与另一边平行的直线,必平分第三边。
几何语言:
在△ ABC中
∵ AD=DB,DE//BC
∴ AE=EC
A
B
C
中点
D
中点
E
F
C
B
A
E
D
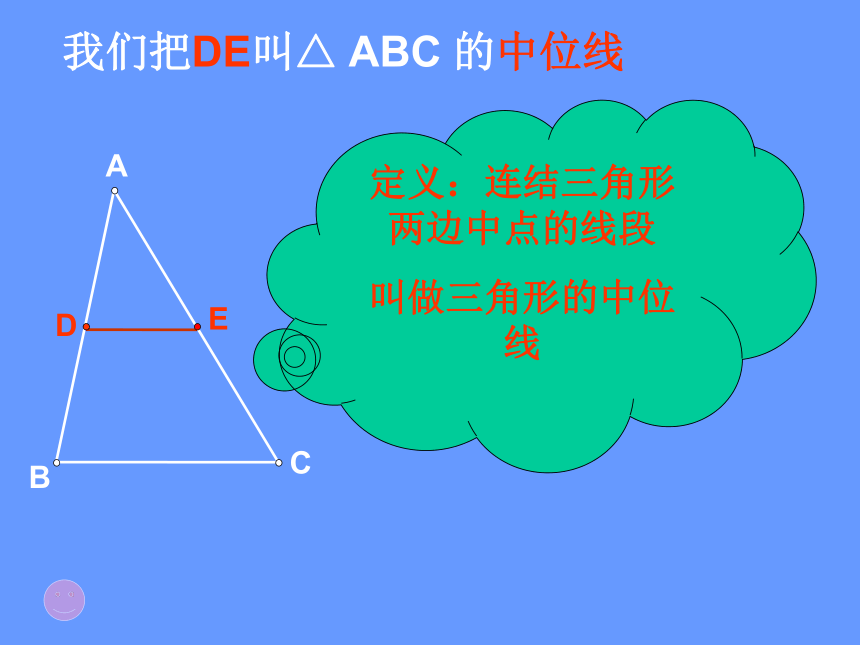
定义:连结三角形两边中点的线段
叫做三角形的中位线
我们把DE叫△ ABC 的中位线
注意:
三角形的中位线是连结三角形两边中点的线段
三角形的中线是连结一个顶点和它的对边中点的线段
三角形的中位线和中线区别:
理解三角形的中位线定义的两层含义:
② ∵ DE为△ABC的中位线
① ∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线
∴ D、E分别为AB、AC的中点
一个三角形共有三条中位线。
定义
A
B
C
D。
。E
。F
A
B
C
D
E
经过三角形一边的中点与另一边平行的直线必平分第三边
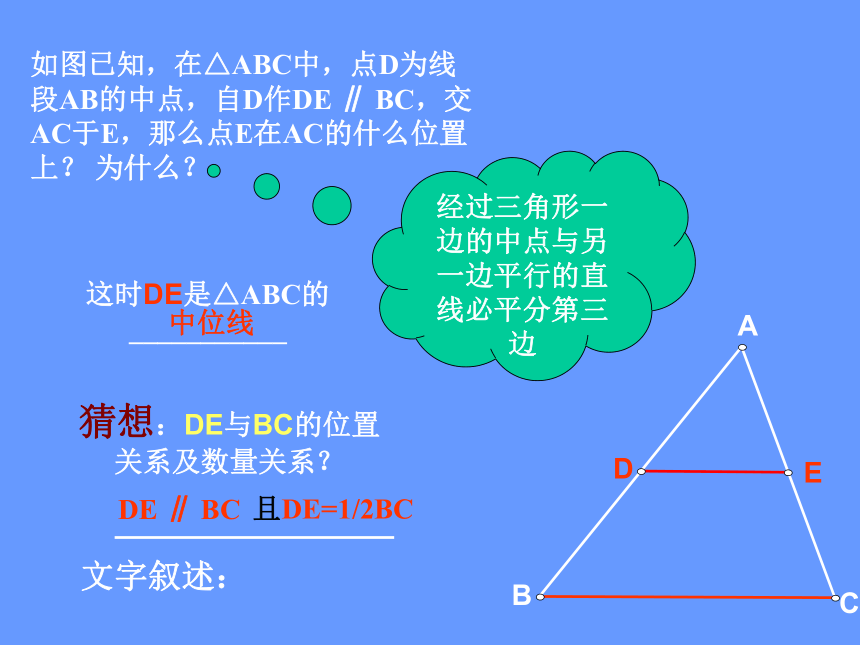
如图已知,在△ABC中,点D为线段AB的中点,自D作DE ∥ BC,交AC于E,那么点E在AC的什么位置上? 为什么?
这时DE是△ABC的___________
中位线
猜想:DE与BC的位置关系及数量关系?
DE ∥ BC
且DE=1/2BC
文字叙述:
过D作DE’∥BC,交AC于E’点
∵D为AB边上的中点
所以DE’与DE重合,因此DE∥BC
同样过D作DF∥AC,交BC于F
∴BF=FC= 1/2BC (经过三角形一边的中点与
另一边平行的直线必平分第三边)
∴四边形DECF是平行四边形
∴DE=FC ∴ DE=1/2BC
∴E’是AC的中点(经过三角形一
边的中点与另一边平行的直线必
平分第三边)
A
B
C
D
E
E’
F
证明方法1.
三角形的中位线平行于第三边,并且等于第三边的 一半
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC
A
B
C
D
E
F
证明方法2.:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥= CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC
A
B
C
E
D
F
A
B
C
E
D
F
常见的三种证法
A
B
C
D
E’
E
F
如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC
① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
用 途
A
B
C
D
E
***中点想到
中线、中位线
1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
2.如图2:在△ABC中,D、E、F分别
是各边中点
EF=3cm,DF=4cm,DE=5cm,
则△ABC的周长= cm
图1
图2
60
4
24
A
B
C
D。
。E
B
A
C
D 。
。E
。F
5
4
3
A 。
。B
C 。
D。
。
E
3. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
20
40
4.例:求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形
求证:四边形EFGH是平行四边形
A
D
C
B
E
F
G
H
证明:连结AC
∵AH=HD CG=GD
∴HG∥AC
(三角形的中位线平行于第三边,并且等于它的一半)
同理EF∥AC
∴HG∥EF且HG=EF
∴四边形EFGH是平行四边形
分别是AB、BC、CD、DA的中点.
已知:在四边形ABCD中,E.F.G.H
【例题】求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。
A
B
C
D
E
F
G
H
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
证明:
连结AC
∵AH=HD,CG=GD
∴HG//AC,HG= AC
(三角形中位线定理)
同理:
EF//AC,EF= AC
且EF=HG
所以四边形EFGH是平行四边形
∴ EF//HG,
(1) 如图,AF=FD=DB,
FG∥DE∥BC,PE=1.5。
则DP= ———,BC= ———。
3
4.5
9
1.5
P
A
B
F
G
E
C
D
(2)已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△ HPN的周长等于—————,为△ ABC周长的——, 面积为△ABC面积的——
B
C
A
D
E
F
H
P
N
提高练习:
4.5
9
3、证明线段倍分关系的方法常有三种:
A
B
C
D
E
中点
中点
(1)三角形中位线定理。
A
B
C
D
中点
(2)直角三角形斜边上的中线等于斜边的一半。
A
B
C
300
(3)直角三角形300角所对的直角边等于斜边的一半。
CD = AB
DE = CB
BC = AB
D
C
B
A
H
G
F
E
⑴在四边形ABCD另加条件AC=BD, 四边形EFGH是_______,为什么?
⑵在四边形ABCD另加条件AC⊥BD,四边形EFGH是_____?为什么?
⑶若四边形EFGH是正方形,AC与BD应满足什么条件?
1. 连结BD 证:EH ∥= FG
2.连结AC、BD ,证:EF∥HG, EH∥FG
3.连结AC、BD, 证:EF=HG,EH=FG
A
B
C
D
E
A
。B
C 。
D 。
。
E
A、B两地被池塘隔开,现在要测量出A、B两地间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将一起探究一种看似不能完成却可以完成的测量的方法。
如图,在A、B外选一点C,连结AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,那么就能知道AB的距离吗?。
今天这堂课我们就要来探究其中的学问。
补充:(1)平行线等分线段定理推论
经过三角形一边的中点与另一边平行的直线,必平分第三边。
几何语言:
在△ ABC中
∵ AD=DB,DE//BC
∴ AE=EC
A
B
C
中点
D
中点
E
F
C
B
A
E
D
定义:连结三角形两边中点的线段
叫做三角形的中位线
我们把DE叫△ ABC 的中位线
注意:
三角形的中位线是连结三角形两边中点的线段
三角形的中线是连结一个顶点和它的对边中点的线段
三角形的中位线和中线区别:
理解三角形的中位线定义的两层含义:
② ∵ DE为△ABC的中位线
① ∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线
∴ D、E分别为AB、AC的中点
一个三角形共有三条中位线。
定义
A
B
C
D。
。E
。F
A
B
C
D
E
经过三角形一边的中点与另一边平行的直线必平分第三边
如图已知,在△ABC中,点D为线段AB的中点,自D作DE ∥ BC,交AC于E,那么点E在AC的什么位置上? 为什么?
这时DE是△ABC的___________
中位线
猜想:DE与BC的位置关系及数量关系?
DE ∥ BC
且DE=1/2BC
文字叙述:
过D作DE’∥BC,交AC于E’点
∵D为AB边上的中点
所以DE’与DE重合,因此DE∥BC
同样过D作DF∥AC,交BC于F
∴BF=FC= 1/2BC (经过三角形一边的中点与
另一边平行的直线必平分第三边)
∴四边形DECF是平行四边形
∴DE=FC ∴ DE=1/2BC
∴E’是AC的中点(经过三角形一
边的中点与另一边平行的直线必
平分第三边)
A
B
C
D
E
E’
F
证明方法1.
三角形的中位线平行于第三边,并且等于第三边的 一半
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC
A
B
C
D
E
F
证明方法2.:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥= CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC
A
B
C
E
D
F
A
B
C
E
D
F
常见的三种证法
A
B
C
D
E’
E
F
如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC
① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2
用 途
A
B
C
D
E
***中点想到
中线、中位线
1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
2.如图2:在△ABC中,D、E、F分别
是各边中点
EF=3cm,DF=4cm,DE=5cm,
则△ABC的周长= cm
图1
图2
60
4
24
A
B
C
D。
。E
B
A
C
D 。
。E
。F
5
4
3
A 。
。B
C 。
D。
。
E
3. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
20
40
4.例:求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形
求证:四边形EFGH是平行四边形
A
D
C
B
E
F
G
H
证明:连结AC
∵AH=HD CG=GD
∴HG∥AC
(三角形的中位线平行于第三边,并且等于它的一半)
同理EF∥AC
∴HG∥EF且HG=EF
∴四边形EFGH是平行四边形
分别是AB、BC、CD、DA的中点.
已知:在四边形ABCD中,E.F.G.H
【例题】求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。
A
B
C
D
E
F
G
H
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
证明:
连结AC
∵AH=HD,CG=GD
∴HG//AC,HG= AC
(三角形中位线定理)
同理:
EF//AC,EF= AC
且EF=HG
所以四边形EFGH是平行四边形
∴ EF//HG,
(1) 如图,AF=FD=DB,
FG∥DE∥BC,PE=1.5。
则DP= ———,BC= ———。
3
4.5
9
1.5
P
A
B
F
G
E
C
D
(2)已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△ HPN的周长等于—————,为△ ABC周长的——, 面积为△ABC面积的——
B
C
A
D
E
F
H
P
N
提高练习:
4.5
9
3、证明线段倍分关系的方法常有三种:
A
B
C
D
E
中点
中点
(1)三角形中位线定理。
A
B
C
D
中点
(2)直角三角形斜边上的中线等于斜边的一半。
A
B
C
300
(3)直角三角形300角所对的直角边等于斜边的一半。
CD = AB
DE = CB
BC = AB
D
C
B
A
H
G
F
E
⑴在四边形ABCD另加条件AC=BD, 四边形EFGH是_______,为什么?
⑵在四边形ABCD另加条件AC⊥BD,四边形EFGH是_____?为什么?
⑶若四边形EFGH是正方形,AC与BD应满足什么条件?
1. 连结BD 证:EH ∥= FG
2.连结AC、BD ,证:EF∥HG, EH∥FG
3.连结AC、BD, 证:EF=HG,EH=FG
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
