青岛版八年级数学下册6.4三角形中位线定理 课件 (共19张PPT)
文档属性
| 名称 | 青岛版八年级数学下册6.4三角形中位线定理 课件 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 16:22:32 | ||
图片预览





文档简介
(共19张PPT)
三角形的中位线
6.4三角形的中位线定理
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。
旧知回顾:
平行四边形的判定方法:
(1)一组对边平行且相等的四边形是平行四边形
(2)两组对边分别相等的四边形是平行四边形
(3)两条对角线互相平分的四边形是平行四边形
(4)两组对边分别平行的四边形是平行四边形
温馨提示
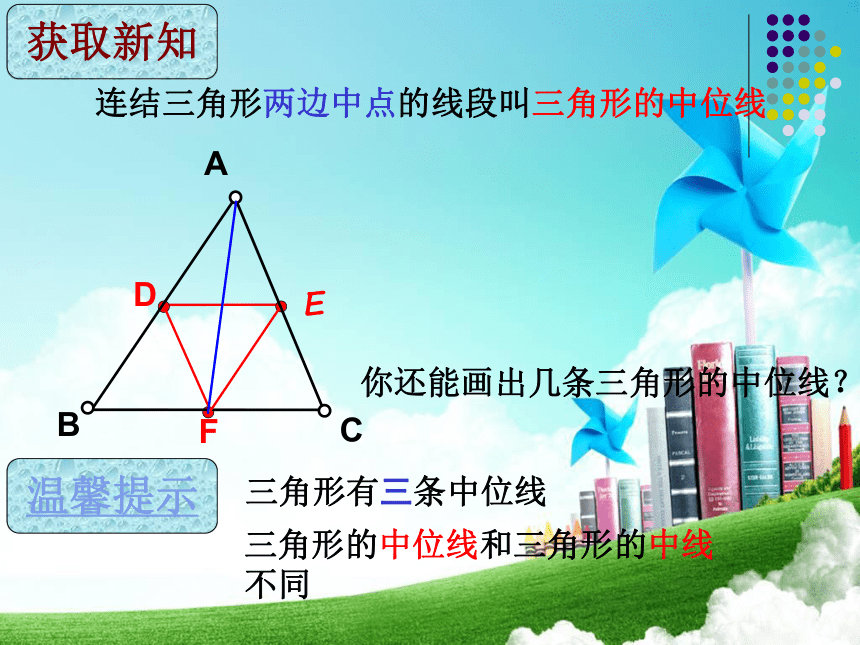
连结三角形两边中点的线段叫三角形的中位线
三角形有三条中位线
三角形的中位线和三角形的中线不同
E
D
F
A
C
B
获取新知
你还能画出几条三角形的中位线?
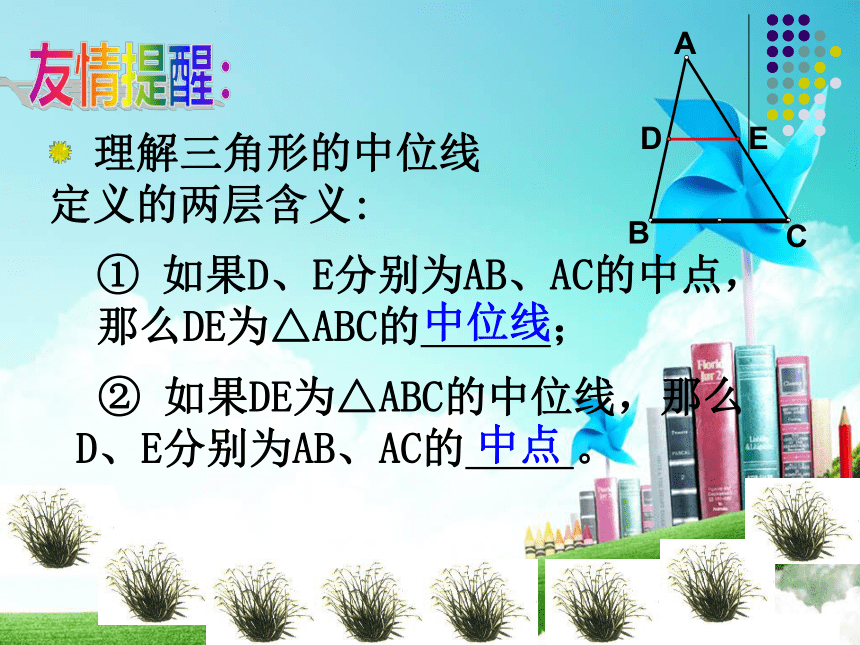
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
A
B
C
将一张三角形硬纸片沿一条中位线剪成两部分,使分成的两部分能拼成一个四边形 是什么形状?
F
四边形BCFD是平行四边形吗 说说你的理由!
三角形的中位线平行且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线
C
E
D
B
A
① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半
用 途
A
C
B
E
D
F
初试身手
若∠ADE=65°,则∠B= 度,为什么?
若BC=8cm,则DE= cm,为什么?
65
4
若AC=4cm,BC=6cmAB=8cm,
则△DEF的周长=______
.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
1、 三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?
探究活动
2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系?
图中有_____个平行四边形
若△ABC的面积为24,△DEF的面积是_____
3
6
已知:如图,在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明。
A
B
C
D
E
F
G
H
E,F是AB,BC的中点,你联想到什么?
要使EF成为一个三角形的中位线应怎样添加辅助线?
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
典例示范
答: 四边形EFGH为平行四边形。
已知: 在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.
求证∠PMN=∠PNM.
已知 ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点。求 证:∠HEF= ∠FGH。
拓展:已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
判断四边形ADFE的形状。
(1)请增加一个条件使得四边形ADFE为菱形。
(2) 请增加一个条件使得四边形ADFE为矩形。
A
B
C
D
E
F
G
H
(3)能不能只增加一个条件使得四边形ADFE为正方形。
结 论
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
它的对角线是否垂直
或者是否相等
它的对角线是否垂直
或者是否相等
(1)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(3)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(2)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
A
B
C
D
A
B
C
D
F
E
G
H
(1) 顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
平行四边形
矩形
(3)顺次连结正方形各边中点所得的四边形是什么?
正方形
(4)顺次连结矩形各边中点所得的四边形是什么?
三角形的中位线
6.4三角形的中位线定理
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。
旧知回顾:
平行四边形的判定方法:
(1)一组对边平行且相等的四边形是平行四边形
(2)两组对边分别相等的四边形是平行四边形
(3)两条对角线互相平分的四边形是平行四边形
(4)两组对边分别平行的四边形是平行四边形
温馨提示
连结三角形两边中点的线段叫三角形的中位线
三角形有三条中位线
三角形的中位线和三角形的中线不同
E
D
F
A
C
B
获取新知
你还能画出几条三角形的中位线?
理解三角形的中位线定义的两层含义:
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;
C
B
A
E
D
中位线
中点
A
B
C
将一张三角形硬纸片沿一条中位线剪成两部分,使分成的两部分能拼成一个四边形 是什么形状?
F
四边形BCFD是平行四边形吗 说说你的理由!
三角形的中位线平行且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线
C
E
D
B
A
① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半
用 途
A
C
B
E
D
F
初试身手
若∠ADE=65°,则∠B= 度,为什么?
若BC=8cm,则DE= cm,为什么?
65
4
若AC=4cm,BC=6cmAB=8cm,
则△DEF的周长=______
.如图,在△ABC中,D、E、F分别是AB、AC、BC的中点
9cm
若△ABC的周长为24,△DEF的周长是_____
12
1、 三角形三条中位线围成的三角形的周长与原三角形的周长有什么关系?
探究活动
2、三角形三条中位线围成的三角形的面积与原三角形的面积有什么关系?
图中有_____个平行四边形
若△ABC的面积为24,△DEF的面积是_____
3
6
已知:如图,在四边形ABCD中,E、F、G、H分别是 AB、BC、CD、DA的中点.
猜想四边形EFGH的形状并证明。
A
B
C
D
E
F
G
H
E,F是AB,BC的中点,你联想到什么?
要使EF成为一个三角形的中位线应怎样添加辅助线?
证明:如图,连接AC
∵EF是△ABC的中位线
同理得:
∴四边形EFGH是平行四边形
典例示范
答: 四边形EFGH为平行四边形。
已知: 在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.
求证∠PMN=∠PNM.
已知 ABCD中,AC、BD相交于点O,E、F、G、H分别是AB、OB、CD、OD的中点。求 证:∠HEF= ∠FGH。
拓展:已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
判断四边形ADFE的形状。
(1)请增加一个条件使得四边形ADFE为菱形。
(2) 请增加一个条件使得四边形ADFE为矩形。
A
B
C
D
E
F
G
H
(3)能不能只增加一个条件使得四边形ADFE为正方形。
结 论
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关.
它的对角线是否垂直
或者是否相等
它的对角线是否垂直
或者是否相等
(1)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(3)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(2)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
A
B
C
D
A
B
C
D
F
E
G
H
(1) 顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
平行四边形
矩形
(3)顺次连结正方形各边中点所得的四边形是什么?
正方形
(4)顺次连结矩形各边中点所得的四边形是什么?
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
