青岛版八年级数学下册6.3特殊的平行四边形 课件(共25张PPT)
文档属性
| 名称 | 青岛版八年级数学下册6.3特殊的平行四边形 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 16:32:22 | ||
图片预览






文档简介
(共25张PPT)
第6章 平行四边形
6.3 特殊的平行四边形(3)
—菱形的性质及判定定理
1. 经历菱形的概念、性质、判定定理的发现过程,掌握菱形的性质定理 “菱形的四条边都相等” ,“菱形的对角线互相垂直, 并且每条对角线平分一组对角” ;
2. 掌握菱形的判定定理“四条边相等的四边形是菱形”,“对角线互相垂直的平行四边形是菱形” ;
3. 能够运用菱形的知识解决简单的具体问题.
前面我们学行四边形和矩形,知道如果平行四边形有一个角是直角时, 成为什么图形
矩形, 由角变化得到
如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢
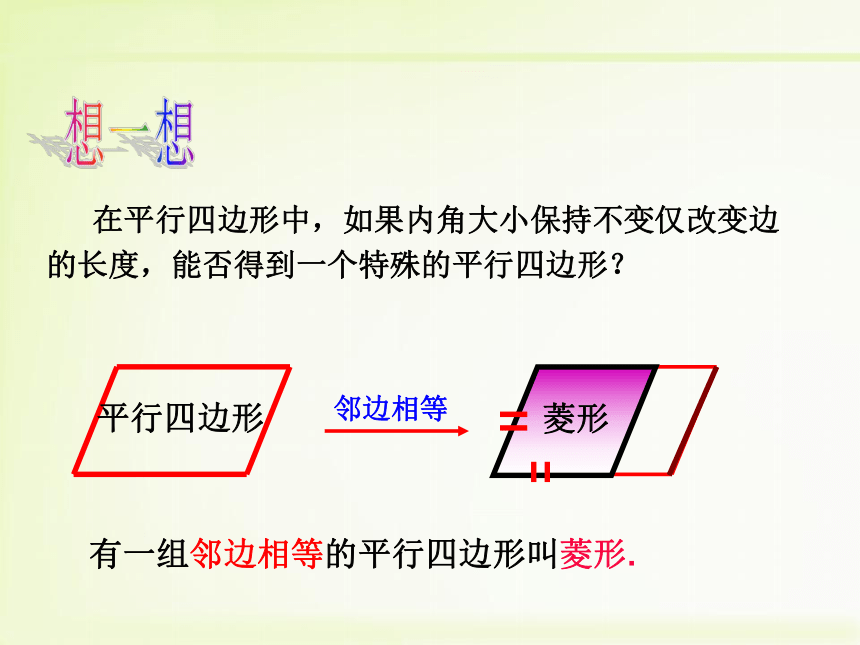
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
有一组邻边相等的平行四边形叫菱形.
菱形
邻边相等
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
B
D
A
C
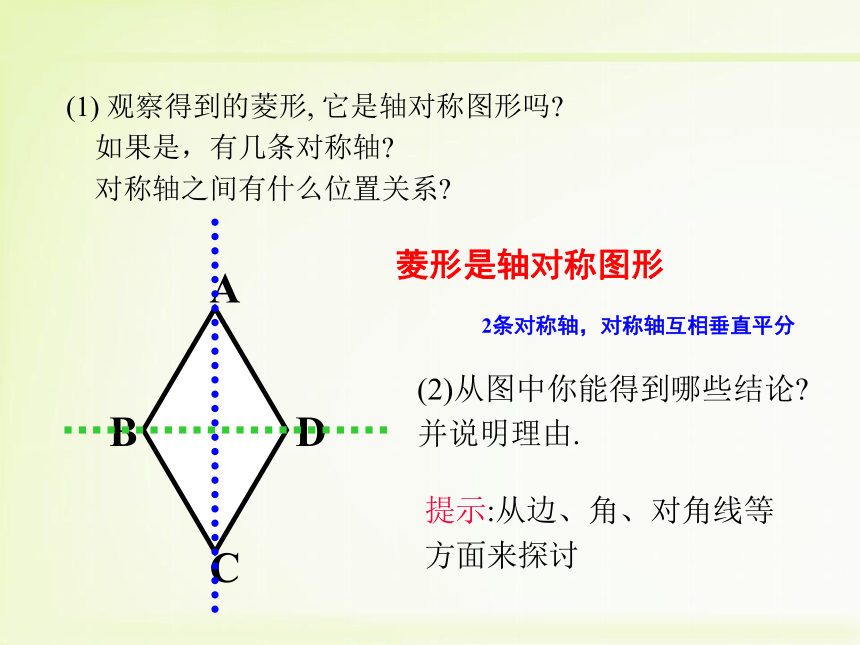
菱形是轴对称图形
(2)从图中你能得到哪些结论 并说明理由.
提示:从边、角、对角线等方面来探讨
(1) 观察得到的菱形, 它是轴对称图形吗
如果是,有几条对称轴
对称轴之间有什么位置关系
2条对称轴,对称轴互相垂直平分
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形是特殊的平行四边形,具有平行四边形的所有性质.
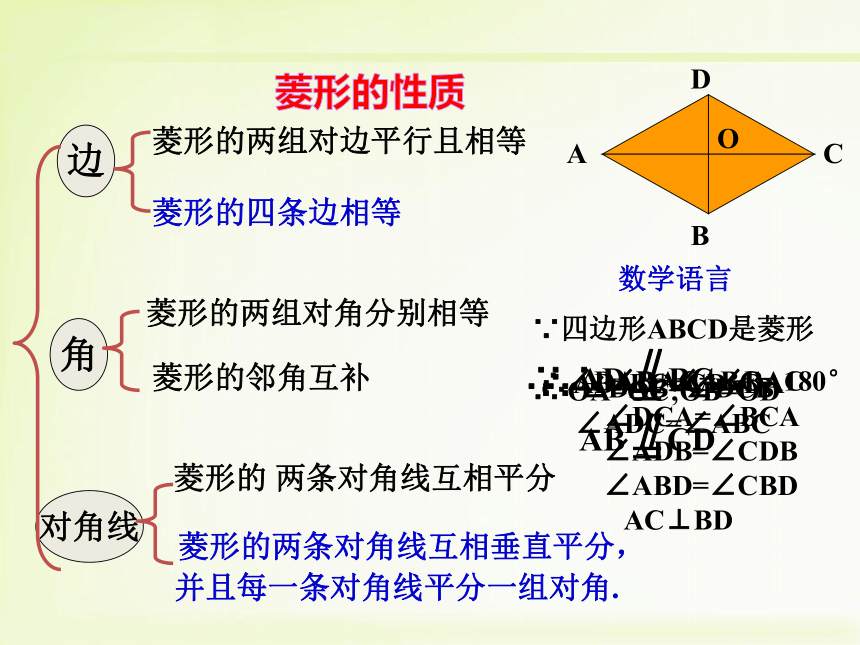
菱形的性质:
B
D
A
C
菱形的性质1:
菱形的四条边都相等.
又:
符号语言
∵四边形ABCD是菱形
∴AB=BC=CD=AD
符号语言
∵四边形ABCD是菱形
∴ AC⊥BD
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC
B
D
A
C
菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
∴ AB=BC=CD=DA
A
D
C
B
O
∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴ OA=OC;OB=OD
∴ ∠DAB=∠DCB
∠ADC=∠ABC
∴ ∠DAB+∠ABC= 180°
已知:如图,菱形ABCD的对角线AC和BD相交于点O.
证明:∵四边形ABCD是菱形
A
B
C
D
O
在△ABD中, BO=DO
∴AB=AD(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC .
证一证
想一想
我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么? 那么类比着它们,菱形的第一种判定方法是什么?
一组邻边相等的平行四边形是菱形.
根据定义得:
命题:有四条边相等的四边形是菱形.
已知:在四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
数学语言
菱形的判定定理1:
探究
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形. 转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ 平行四边形ABCD是菱形
求证:平行四边形ABCD是菱形
已知:在平行四边形ABCD中,AC ⊥ BD
对角线互相垂直的平行四边形是菱形.
数学语言
菱形的判定定理2:
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
AC⊥BD
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
+ 邻边相等 =
+对角线线互相垂直 =
四条边相等 + =
下列三个图形都是菱形, 正确吗 为什么?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
3
3
4
4
┍
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可. 你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
A
B
C
D
E
F
1、如图,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠ EAF=60°, ∠ BAE=18°, 求∠ CEF的度数.
2、已知:如图, 四边形ABCD是边长为13cm的菱形, 其中对角线BD长10cm.
求: (1)对角线AC的长度 (2)菱形的面积
解: (1)
∵四边形ABCD是菱形,
∴∠AED=90°,
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
=2×△ABD的面积
解:(2) 菱形ABCD的面积
=△ABD的面积+△CBD的面积
求: (2)菱形的面积
D
B
C
A
E
由此可进一步推导得出:
对角线互相垂直的四边形的面积都等于两条对角线乘积的一半.
1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?
习题P26,练习第1、2题.
作 业
四边形集合
平行四边形集合
菱形集合
矩形集合
第6章 平行四边形
6.3 特殊的平行四边形(3)
—菱形的性质及判定定理
1. 经历菱形的概念、性质、判定定理的发现过程,掌握菱形的性质定理 “菱形的四条边都相等” ,“菱形的对角线互相垂直, 并且每条对角线平分一组对角” ;
2. 掌握菱形的判定定理“四条边相等的四边形是菱形”,“对角线互相垂直的平行四边形是菱形” ;
3. 能够运用菱形的知识解决简单的具体问题.
前面我们学行四边形和矩形,知道如果平行四边形有一个角是直角时, 成为什么图形
矩形, 由角变化得到
如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
有一组邻边相等的平行四边形叫菱形.
菱形
邻边相等
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
B
D
A
C
菱形是轴对称图形
(2)从图中你能得到哪些结论 并说明理由.
提示:从边、角、对角线等方面来探讨
(1) 观察得到的菱形, 它是轴对称图形吗
如果是,有几条对称轴
对称轴之间有什么位置关系
2条对称轴,对称轴互相垂直平分
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质:
B
D
A
C
菱形的性质1:
菱形的四条边都相等.
又:
符号语言
∵四边形ABCD是菱形
∴AB=BC=CD=AD
符号语言
∵四边形ABCD是菱形
∴ AC⊥BD
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC
B
D
A
C
菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
∴ AB=BC=CD=DA
A
D
C
B
O
∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴ OA=OC;OB=OD
∴ ∠DAB=∠DCB
∠ADC=∠ABC
∴ ∠DAB+∠ABC= 180°
已知:如图,菱形ABCD的对角线AC和BD相交于点O.
证明:∵四边形ABCD是菱形
A
B
C
D
O
在△ABD中, BO=DO
∴AB=AD(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC .
证一证
想一想
我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么? 那么类比着它们,菱形的第一种判定方法是什么?
一组邻边相等的平行四边形是菱形.
根据定义得:
命题:有四条边相等的四边形是菱形.
已知:在四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形
D
A
B
C
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
数学语言
菱形的判定定理1:
探究
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形. 转动木条,这个四边形什么时候变成菱形
猜想:
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ 平行四边形ABCD是菱形
求证:平行四边形ABCD是菱形
已知:在平行四边形ABCD中,AC ⊥ BD
对角线互相垂直的平行四边形是菱形.
数学语言
菱形的判定定理2:
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
AC⊥BD
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
+ 邻边相等 =
+对角线线互相垂直 =
四条边相等 + =
下列三个图形都是菱形, 正确吗 为什么?
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形
3
3
4
4
┍
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可. 你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
A
B
C
D
E
F
1、如图,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠ EAF=60°, ∠ BAE=18°, 求∠ CEF的度数.
2、已知:如图, 四边形ABCD是边长为13cm的菱形, 其中对角线BD长10cm.
求: (1)对角线AC的长度 (2)菱形的面积
解: (1)
∵四边形ABCD是菱形,
∴∠AED=90°,
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
=2×△ABD的面积
解:(2) 菱形ABCD的面积
=△ABD的面积+△CBD的面积
求: (2)菱形的面积
D
B
C
A
E
由此可进一步推导得出:
对角线互相垂直的四边形的面积都等于两条对角线乘积的一半.
1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?
习题P26,练习第1、2题.
作 业
四边形集合
平行四边形集合
菱形集合
矩形集合
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
