2013年中考数学第一轮总复习几何第6课勾股定理
文档属性
| 名称 | 2013年中考数学第一轮总复习几何第6课勾股定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 209.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-17 00:00:00 | ||
图片预览


文档简介
2013年梅州市中考数学第一轮总复习几何第(6)课 勾股定理
学校:___________________ 姓名:___________________
一、学习目标
1、理解勾股定理;
2、掌握勾股数的计算。
二、学习指导(用约5分钟时间复习知识点,之后用约10分钟完成思考题和达标题)
三、复习(时间:约5分钟)
1、勾股定理
(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2. (2)勾股定理公式a2+b2=c2?的变形有:a=√(c2-b2), b=√(c2-a2)及c=√(a2+b2).
(3)由于a2+b2=c2>a2,所以c>a,同理c>b,即直角三角形的斜边大于该直角三角形中的每一条直角边.
(4)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
(5)由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正方形,以斜边为边长的正方形的
面积等于以直角边为边长的正方形的面积和.
(6)勾股定理的证明图:
2、勾股数
(1)满足a2+b2=c2?的三个正整数,称为勾股数.
(2)一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.
常用的勾股数:①3,4,5(32=4+5);6,8,10;9,12,15 最大的数习惯放在最后.
②5,12,13(52=12+13)
③7, 24,25(72=24+25)
(3)类勾股数:不再限制“正整数”.
常用的类勾股数:①1,1, √2 ②1, √3,2 ③1,2, √5
(4)分式型勾股数:充分利用转化思想.
①4,5/3,c 化成 12/3,5/3,c,因为勾股数5,12,13,所以c=13/3.
a
b
c
a
b
c
1
4
4
4√2
1
2
1
4
4
4√2
1
2
√2
2√2
2√2
4
√2
2
a
b
c
a
b
c
1
4
4√3
8
1
2
√3
4√3/3
4
8√3/3
√3
2
2
2
2√3
4
2
2
a
b
c
a
b
c
1
4
8
4√5
1
2
2
2
4
2√5
2
2
√5
4√5/5
8√5/5
4
√5
2
思考题:1、看例填表格。
2、模仿例题求解勾股数:①10,20,c ②2,3/2,c
例①100,100,c 先化简成:1,1,c/100,由1,1,√2可得c/100=√2,所以c=100√2.
例②4,5/3,c 化成 12/3,5/3,c,因为勾股数5,12,13,所以c=13/3.
四、达标题(时间:约10分钟)
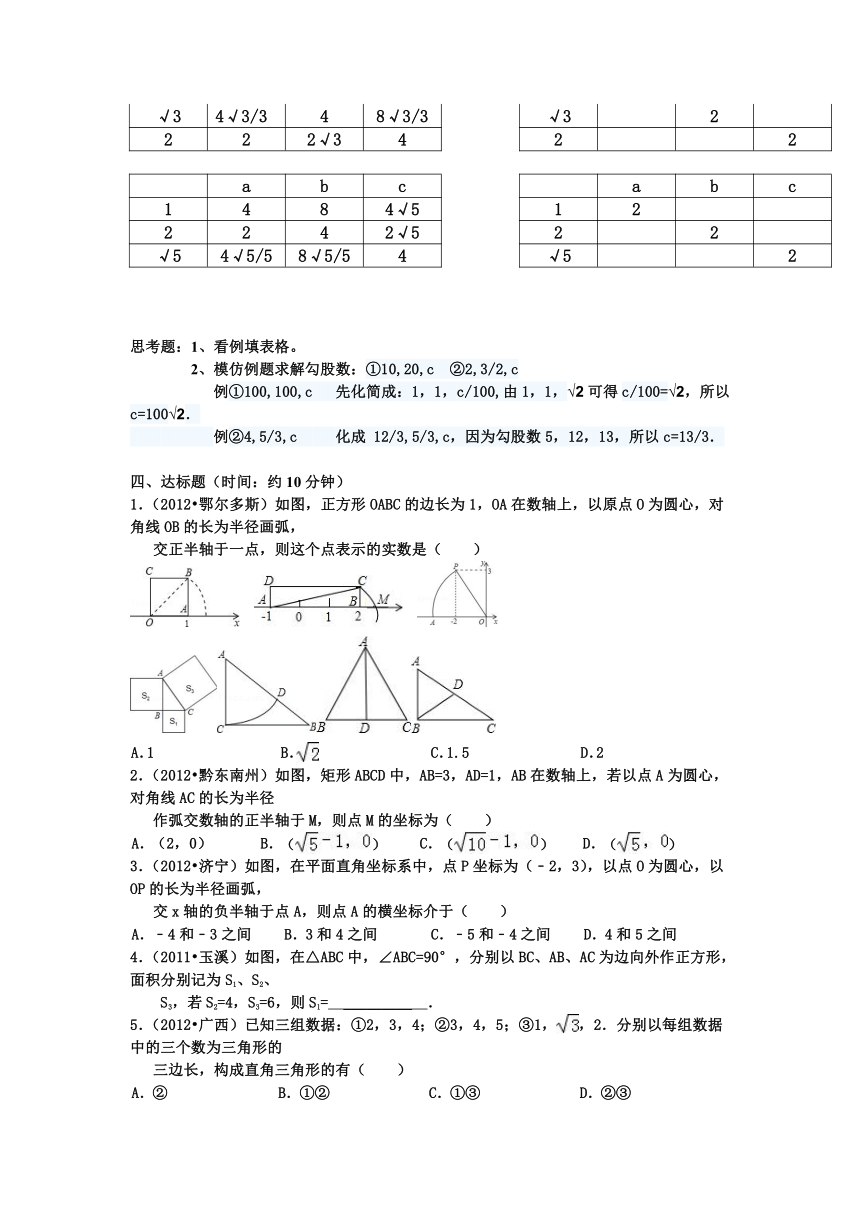
1.(2012?鄂尔多斯)如图,正方形OABC的边长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,
交正半轴于一点,则这个点表示的实数是( )
A.
1
B.
C.
1.5
D.
2
2.(2012?黔东南州)如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径
作弧交数轴的正半轴于M,则点M的坐标为( )
A.
(2,0)
B.
()
C.
()
D.
()
3.(2012?济宁)如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,
交x轴的负半轴于点A,则点A的横坐标介于( )
A.
﹣4和﹣3之间
B.
3和4之间
C.
﹣5和﹣4之间
D.
4和5之间
4.(2011?玉溪)如图,在△ABC中,∠ABC=90°,分别以BC、AB、AC为边向外作正方形,面积分别记为S1、S2、
S3,若S2=4,S3=6,则S1= _________ .
5.(2012?广西)已知三组数据:①2,3,4;②3,4,5;③1,,2.分别以每组数据中的三个数为三角形的
三边长,构成直角三角形的有( )
A.
②
B.
①②
C.
①③
D.
②③
6.(2012?吉林)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于
点D,则BD= _________ .
7.(2011?怀化)如图,在△ABC中,AB=AC,∠BAC的角平分线交BC边于点D,AB=5,BC=6,则AD= _________ .
8.(2009?遂宁)如图,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为 ___ cm.
9.(2007?随州)如图,由四个全等的直角三角形拼成“赵爽弦图”.Rt△ABF中,∠AFB=90°,AF=4,AB=5.
四边形EFGH的面积是 _________ .
10.(2007?荆州)我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的
一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为
a、b,那么(a+b)2的值是 _________ .
五、师生讨论(时间:约10分钟)
学校:___________________ 姓名:___________________ 成绩:____________________
六、反馈(时间:约20分钟)
<一>、必做题
1.(2011?遵义)如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,
则△ABC中BC边上的高是 _________ .
2.(2011?肇庆)在直角三角形ABC中,∠C=90°,BC=12,AC=9,则AB= _________ .
3.(2012?广州)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.
B.
C.
D.
4.(2011?哈尔滨)如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,DE⊥AC,垂足为E,若DE=2,CD=,
则BE的长为 _________ .
5.(2010?铁岭)如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,
经测量AB=2米,则树高为( )
A.
米
B.
米
C.
(+1)米
D.
3米
6.(2012?巴中)已知a、b、c是△ABC的三边长,且满足关系式+|a﹣b|=0,则△ABC的形状为 _________ .
7.(2012?怀化)等腰三角形的底边长为6,底边上的中线长为4,它的腰长为( )
A.
7
B.
6
C.
5
D.
4
8.(2012?佳木斯)等腰三角形一腰长为5,一边上的高为3,则底边长为 _________ .
9.(2012?莱芜)在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是 _________ .
10.(2006?青岛)如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,
得到△P′AB,则点P与P′之间的距离为PP′= _________ ,∠APB= _________ 度.
11.(2011?潍坊)已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O作BD垂直平分线EF,分别交AD、BC
于点E、F,则AE的长为 _________ .
12.(2012?新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积,S2=2π,
则S3是 _________ .
学校:___________________ 姓名:___________________ 成绩:____________________
<二>、选做题
1.(2012?黔西南州)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则
四边形ACEB的周长为 _________ .
2.(2011?杭州)在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线l∥AB,F是l上的一点,且AB=AF,则点F
到直线BC的距离为 _________ .
3.(2010?山西)如图,在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,则DE的长是 _________ .
4.(2011?山西)如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长是 _________ .
5.(2011?鸡西)已知三角形相邻两边长分别为20cm和30cm,第三边上的高为10cm,则此三角形的面积为_________
cm2.
6.(2012?宁波)勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”
的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由
图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ
的面积为( )
A.
90
B.
100
C.
110
D.
121
7.(2010?温州)勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了二枚以勾股图为背景的
邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,
已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,
F在边PQ上,那么△PQR的周长等于 _________ .
8.(2011?温州)我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”
(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,
正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是 _________ .
学校:___________________ 姓名:___________________
一、学习目标
1、理解勾股定理;
2、掌握勾股数的计算。
二、学习指导(用约5分钟时间复习知识点,之后用约10分钟完成思考题和达标题)
三、复习(时间:约5分钟)
1、勾股定理
(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2. (2)勾股定理公式a2+b2=c2?的变形有:a=√(c2-b2), b=√(c2-a2)及c=√(a2+b2).
(3)由于a2+b2=c2>a2,所以c>a,同理c>b,即直角三角形的斜边大于该直角三角形中的每一条直角边.
(4)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
(5)由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正方形,以斜边为边长的正方形的
面积等于以直角边为边长的正方形的面积和.
(6)勾股定理的证明图:
2、勾股数
(1)满足a2+b2=c2?的三个正整数,称为勾股数.
(2)一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.
常用的勾股数:①3,4,5(32=4+5);6,8,10;9,12,15 最大的数习惯放在最后.
②5,12,13(52=12+13)
③7, 24,25(72=24+25)
(3)类勾股数:不再限制“正整数”.
常用的类勾股数:①1,1, √2 ②1, √3,2 ③1,2, √5
(4)分式型勾股数:充分利用转化思想.
①4,5/3,c 化成 12/3,5/3,c,因为勾股数5,12,13,所以c=13/3.
a
b
c
a
b
c
1
4
4
4√2
1
2
1
4
4
4√2
1
2
√2
2√2
2√2
4
√2
2
a
b
c
a
b
c
1
4
4√3
8
1
2
√3
4√3/3
4
8√3/3
√3
2
2
2
2√3
4
2
2
a
b
c
a
b
c
1
4
8
4√5
1
2
2
2
4
2√5
2
2
√5
4√5/5
8√5/5
4
√5
2
思考题:1、看例填表格。
2、模仿例题求解勾股数:①10,20,c ②2,3/2,c
例①100,100,c 先化简成:1,1,c/100,由1,1,√2可得c/100=√2,所以c=100√2.
例②4,5/3,c 化成 12/3,5/3,c,因为勾股数5,12,13,所以c=13/3.
四、达标题(时间:约10分钟)
1.(2012?鄂尔多斯)如图,正方形OABC的边长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,
交正半轴于一点,则这个点表示的实数是( )
A.
1
B.
C.
1.5
D.
2
2.(2012?黔东南州)如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径
作弧交数轴的正半轴于M,则点M的坐标为( )
A.
(2,0)
B.
()
C.
()
D.
()
3.(2012?济宁)如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,
交x轴的负半轴于点A,则点A的横坐标介于( )
A.
﹣4和﹣3之间
B.
3和4之间
C.
﹣5和﹣4之间
D.
4和5之间
4.(2011?玉溪)如图,在△ABC中,∠ABC=90°,分别以BC、AB、AC为边向外作正方形,面积分别记为S1、S2、
S3,若S2=4,S3=6,则S1= _________ .
5.(2012?广西)已知三组数据:①2,3,4;②3,4,5;③1,,2.分别以每组数据中的三个数为三角形的
三边长,构成直角三角形的有( )
A.
②
B.
①②
C.
①③
D.
②③
6.(2012?吉林)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于
点D,则BD= _________ .
7.(2011?怀化)如图,在△ABC中,AB=AC,∠BAC的角平分线交BC边于点D,AB=5,BC=6,则AD= _________ .
8.(2009?遂宁)如图,已知△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为 ___ cm.
9.(2007?随州)如图,由四个全等的直角三角形拼成“赵爽弦图”.Rt△ABF中,∠AFB=90°,AF=4,AB=5.
四边形EFGH的面积是 _________ .
10.(2007?荆州)我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的
一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为
a、b,那么(a+b)2的值是 _________ .
五、师生讨论(时间:约10分钟)
学校:___________________ 姓名:___________________ 成绩:____________________
六、反馈(时间:约20分钟)
<一>、必做题
1.(2011?遵义)如图,由四个边长为1的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,
则△ABC中BC边上的高是 _________ .
2.(2011?肇庆)在直角三角形ABC中,∠C=90°,BC=12,AC=9,则AB= _________ .
3.(2012?广州)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A.
B.
C.
D.
4.(2011?哈尔滨)如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,DE⊥AC,垂足为E,若DE=2,CD=,
则BE的长为 _________ .
5.(2010?铁岭)如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,
经测量AB=2米,则树高为( )
A.
米
B.
米
C.
(+1)米
D.
3米
6.(2012?巴中)已知a、b、c是△ABC的三边长,且满足关系式+|a﹣b|=0,则△ABC的形状为 _________ .
7.(2012?怀化)等腰三角形的底边长为6,底边上的中线长为4,它的腰长为( )
A.
7
B.
6
C.
5
D.
4
8.(2012?佳木斯)等腰三角形一腰长为5,一边上的高为3,则底边长为 _________ .
9.(2012?莱芜)在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是 _________ .
10.(2006?青岛)如图,P是正△ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,
得到△P′AB,则点P与P′之间的距离为PP′= _________ ,∠APB= _________ 度.
11.(2011?潍坊)已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O作BD垂直平分线EF,分别交AD、BC
于点E、F,则AE的长为 _________ .
12.(2012?新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积,S2=2π,
则S3是 _________ .
学校:___________________ 姓名:___________________ 成绩:____________________
<二>、选做题
1.(2012?黔西南州)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则
四边形ACEB的周长为 _________ .
2.(2011?杭州)在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线l∥AB,F是l上的一点,且AB=AF,则点F
到直线BC的距离为 _________ .
3.(2010?山西)如图,在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,则DE的长是 _________ .
4.(2011?山西)如图,已知AB=12;AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长是 _________ .
5.(2011?鸡西)已知三角形相邻两边长分别为20cm和30cm,第三边上的高为10cm,则此三角形的面积为_________
cm2.
6.(2012?宁波)勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”
的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由
图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ
的面积为( )
A.
90
B.
100
C.
110
D.
121
7.(2010?温州)勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了二枚以勾股图为背景的
邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,
已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,
F在边PQ上,那么△PQR的周长等于 _________ .
8.(2011?温州)我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”
(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,
正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是 _________ .
同课章节目录
