2013年中考数学总复习第一轮第2课整式公式
文档属性
| 名称 | 2013年中考数学总复习第一轮第2课整式公式 |  | |
| 格式 | zip | ||
| 文件大小 | 88.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-17 11:52:25 | ||
图片预览

文档简介
2013年梅州市中考数学第一轮总复习 第(2)课 整式公式
学校:___________________ 姓名:___________________
一、学习目标
1、掌握平方差公式和完全平方公式;
2、掌握整式混合运算。
二、学习指导(用约5分钟时间复习知识点,之后用约10分钟完成思考题和达标题)
三、复习(时间:约5分钟)
1、整式 a3+b3=(a+b)(a2﹣ab+b2); a3﹣b3=(a﹣b)(a2+ab+b2)
(1)概念:单项式和多项式统称为整式.凡分母中含有字母的代数式都不属于整式.
(2)单项式:数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.
形如a或-a这样的式子的系数是1或-1,不能误以为没有系数.
(3)多项式:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.
2、重要公式 (﹣x﹣y)2=(x+y)2 (﹣x+y)2=(y﹣x)2 x2+2x-1=0两边除以x得 x+2-1/x=0, x-1/x=-2
(1)平方差公式:(a+b)(a-b)=a2-b2两个数的和与这两个数的差相乘,等于这两个数的平方差.
左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
右边是相同项的平方减去相反项的平方;公式中的a和b可以是具体数,也可以是单项式或多项式.
(2)完全平方公式:(a±b)2=a2±2ab+b2.可巧记为:“首平方,末平方,首末两倍中间放”.
左边是两个数的和的平方;右边是一个三项式,其中首末两项分别是两项的平方,都为正,
中间一项是两项积的2倍;其符号与左边的运算符号相同.
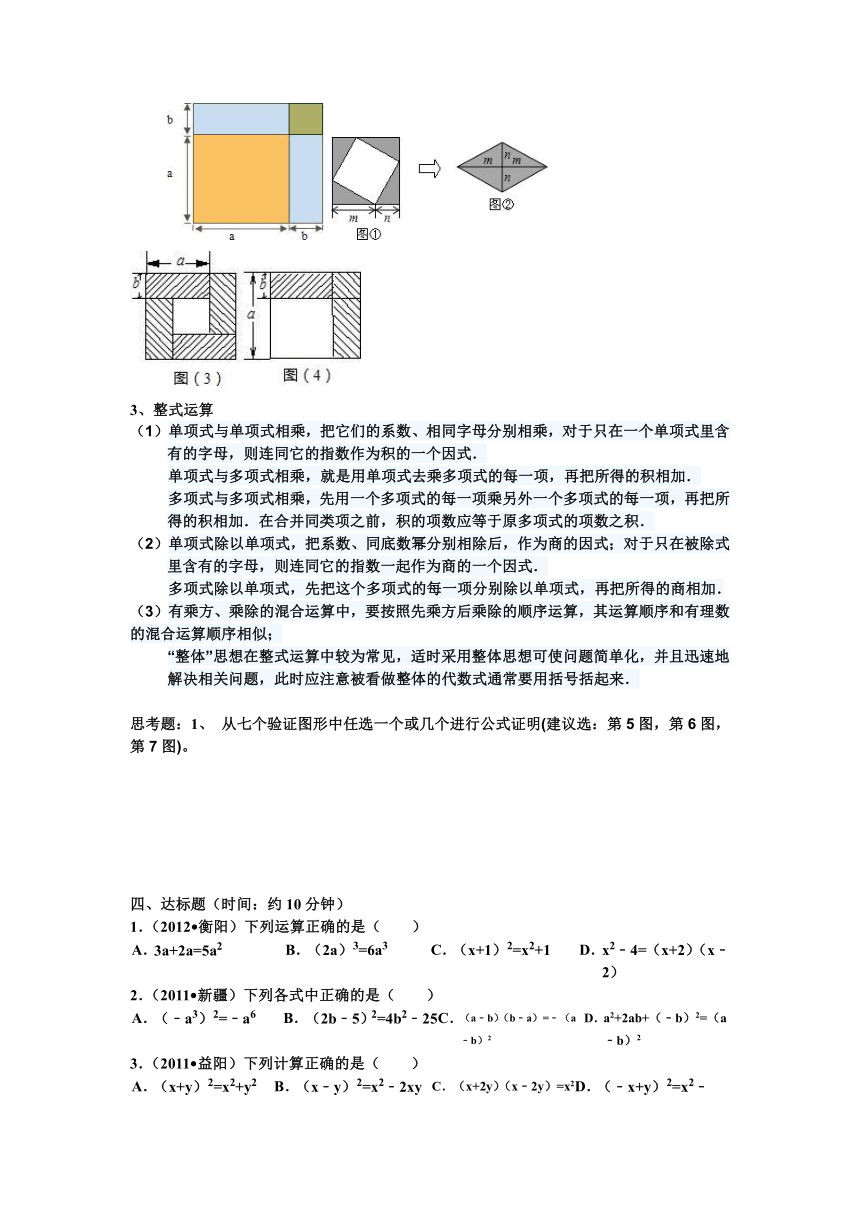
推论:(a+b)2-(a-b)2=4ab(图3).对形如两数和(或差)的平方的计算,都可以用完全平方公式;
对于三项的,把其中的两项看做一项后,也可以用完全平方公式.
3、整式运算
(1)单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.在合并同类项之前,积的项数应等于原多项式的项数之积.
(2)单项式除以单项式,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
(3)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似;
“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.
思考题:1、 从七个验证图形中任选一个或几个进行公式证明(建议选:第5图,第6图,第7图)。
四、达标题(时间:约10分钟)
1.(2012?衡阳)下列运算正确的是( )
A.
3a+2a=5a2
B.
(2a)3=6a3
C.
(x+1)2=x2+1
D.
x2﹣4=(x+2)(x﹣2)
2.(2011?新疆)下列各式中正确的是( )
A.
(﹣a3)2=﹣a6
B.
(2b﹣5)2=4b2﹣25
C.
(a﹣b)(b﹣a)=﹣(a﹣b)2
D.
a2+2ab+(﹣b)2=(a﹣b)2
3.(2011?益阳)下列计算正确的是( )
A.
(x+y)2=x2+y2
B.
(x﹣y)2=x2﹣2xy﹣y2
C.
(x+2y)(x﹣2y)=x2﹣2y2
D.
(﹣x+y)2=x2﹣2xy+y2
4.(2009?枣庄)若m+n=3,则2m2+4mn+2n2﹣6的值为( )
A.
12
B.
6
C.
3
D.
0
5.(2012?镇江)化简:(m+1)2﹣m2= ______ ___ .
6.(﹣x﹣y)2= ______ ___ .
7.(2012?厦门)已知a+b=2,ab=﹣1,则3a+ab+3b= ____ _____ ;a2+b2= _____ ____ .
8.(2004?宁波)若x+y=5,x﹣y=1,则xy= ____ _____ .
9.(2009?嘉兴)化简:(a+2b)(a﹣2b)﹣b(a﹣8b)
10.(2002?徐州)计算:(2ab2)3﹣(9ab2)?(﹣ab2)2
五、师生讨论(时间:约10分钟)
学校:___________________ 姓名:___________________ 成绩:____________________
六、反馈(时间:约20分钟)
<一>、必做题
1.将多项式4x2+1加上单项式 ________ _ 后,使它成为另一个整式的完全平方(请写出所有可能的情况).
2.(2010?怀化)若x=1,,则x2+4xy+4y2的值是( )
A.
2
B.
4
C.
D.
3.(2012?常州)已知x=y+4,则代数式x2﹣2xy+y2﹣25的值为 _________ .
4.(2012?遵义)已知x+y=﹣5,xy=6,则x2+y2= ___ _ _____ .
5.计算:1232﹣122×124= _ ________ .
6.计算:832+83×34+172= ______ ___ .
7.计算20002﹣4000×1999+19992= _______ __ .
8.用完全平方公式填空:4﹣12(x﹣y)+9(x﹣y)2=( _________ )2.
9.(2011?大庆)若,则= ______ ___ .
10.已知x,则x= _________ .
11.(2012?凉山州)整式A与m2﹣2mn+n2的和是(m+n)2,则A= _____ ____ .
12.(2001?天津)已知x+y=4,且x﹣y=10,则2xy= ___ ______ .
13.(2005?威海)若a+b=6,ab=4,则a﹣b= _____ ____ .
14.(2007?天津)已知x+y=7且xy=12,则当x<y时,的值等于 _________ .
15.(2012?江西)已知(m﹣n)2=8,(m+n)2=2,则m2+n2= _____ ____ .
16.(2003?徐州)计算:(3a2b)2+(8a6b2)÷(﹣2a2b)
17.计算:a×(3a2b)3÷(﹣)×
18.计算:3a3b2÷a2+b?(a2b﹣3ab﹣5a2b)
19.计算:[x(x2y2﹣xy)﹣y(x2+x3y)]÷3x2y.
学校:___________________ 姓名:___________________ 成绩:____________________
<二>、选做题
1.(2+1)(22+1)(24+1)的结果为 _________ .
2.(2009?北京)若把代数式x2﹣2x﹣3化为(x﹣m)2+k的形式,其中m,k为常数,则m+k= _________ .
3.计算:= _________ .
4.(2004?天津)已知x2+y2=25,x+y=7,且x>y,则x﹣y的值等于 _________ .
5.已知(2009﹣a)(2008﹣a)=2007,那么(2009﹣a)2+(2008﹣a)2= _________ .
6.(2009?烟台)设a>b>0,a2+b2﹣6ab=0,则的值等于 _________ .
7.若x﹣y=2,x2+y2=4,则x2004+y2004的值是 _________ .
8.(2011?乐山)若m为正实数,且,则= _____ ____ .
9.(2011?天津)若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是( )
A.
x+y+z=0
B.
x+y﹣2z=0
C.
y+z﹣2x=0
D.
z+x﹣2y=0
10.(2010?内江)已知m2﹣5m﹣1=0,则= _________ .
11.(2011?达州)若,则= _________ .
12.(2001?常州)已知x+y=1,则代数式x3+3xy+y3的值是 _________ .
13.计算:4x(x﹣1)2+x(2x+5)(5﹣2x)= _______ __ .
学校:___________________ 姓名:___________________
一、学习目标
1、掌握平方差公式和完全平方公式;
2、掌握整式混合运算。
二、学习指导(用约5分钟时间复习知识点,之后用约10分钟完成思考题和达标题)
三、复习(时间:约5分钟)
1、整式 a3+b3=(a+b)(a2﹣ab+b2); a3﹣b3=(a﹣b)(a2+ab+b2)
(1)概念:单项式和多项式统称为整式.凡分母中含有字母的代数式都不属于整式.
(2)单项式:数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式.
形如a或-a这样的式子的系数是1或-1,不能误以为没有系数.
(3)多项式:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.
2、重要公式 (﹣x﹣y)2=(x+y)2 (﹣x+y)2=(y﹣x)2 x2+2x-1=0两边除以x得 x+2-1/x=0, x-1/x=-2
(1)平方差公式:(a+b)(a-b)=a2-b2两个数的和与这两个数的差相乘,等于这两个数的平方差.
左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
右边是相同项的平方减去相反项的平方;公式中的a和b可以是具体数,也可以是单项式或多项式.
(2)完全平方公式:(a±b)2=a2±2ab+b2.可巧记为:“首平方,末平方,首末两倍中间放”.
左边是两个数的和的平方;右边是一个三项式,其中首末两项分别是两项的平方,都为正,
中间一项是两项积的2倍;其符号与左边的运算符号相同.
推论:(a+b)2-(a-b)2=4ab(图3).对形如两数和(或差)的平方的计算,都可以用完全平方公式;
对于三项的,把其中的两项看做一项后,也可以用完全平方公式.
3、整式运算
(1)单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.在合并同类项之前,积的项数应等于原多项式的项数之积.
(2)单项式除以单项式,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
(3)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似;
“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.
思考题:1、 从七个验证图形中任选一个或几个进行公式证明(建议选:第5图,第6图,第7图)。
四、达标题(时间:约10分钟)
1.(2012?衡阳)下列运算正确的是( )
A.
3a+2a=5a2
B.
(2a)3=6a3
C.
(x+1)2=x2+1
D.
x2﹣4=(x+2)(x﹣2)
2.(2011?新疆)下列各式中正确的是( )
A.
(﹣a3)2=﹣a6
B.
(2b﹣5)2=4b2﹣25
C.
(a﹣b)(b﹣a)=﹣(a﹣b)2
D.
a2+2ab+(﹣b)2=(a﹣b)2
3.(2011?益阳)下列计算正确的是( )
A.
(x+y)2=x2+y2
B.
(x﹣y)2=x2﹣2xy﹣y2
C.
(x+2y)(x﹣2y)=x2﹣2y2
D.
(﹣x+y)2=x2﹣2xy+y2
4.(2009?枣庄)若m+n=3,则2m2+4mn+2n2﹣6的值为( )
A.
12
B.
6
C.
3
D.
0
5.(2012?镇江)化简:(m+1)2﹣m2= ______ ___ .
6.(﹣x﹣y)2= ______ ___ .
7.(2012?厦门)已知a+b=2,ab=﹣1,则3a+ab+3b= ____ _____ ;a2+b2= _____ ____ .
8.(2004?宁波)若x+y=5,x﹣y=1,则xy= ____ _____ .
9.(2009?嘉兴)化简:(a+2b)(a﹣2b)﹣b(a﹣8b)
10.(2002?徐州)计算:(2ab2)3﹣(9ab2)?(﹣ab2)2
五、师生讨论(时间:约10分钟)
学校:___________________ 姓名:___________________ 成绩:____________________
六、反馈(时间:约20分钟)
<一>、必做题
1.将多项式4x2+1加上单项式 ________ _ 后,使它成为另一个整式的完全平方(请写出所有可能的情况).
2.(2010?怀化)若x=1,,则x2+4xy+4y2的值是( )
A.
2
B.
4
C.
D.
3.(2012?常州)已知x=y+4,则代数式x2﹣2xy+y2﹣25的值为 _________ .
4.(2012?遵义)已知x+y=﹣5,xy=6,则x2+y2= ___ _ _____ .
5.计算:1232﹣122×124= _ ________ .
6.计算:832+83×34+172= ______ ___ .
7.计算20002﹣4000×1999+19992= _______ __ .
8.用完全平方公式填空:4﹣12(x﹣y)+9(x﹣y)2=( _________ )2.
9.(2011?大庆)若,则= ______ ___ .
10.已知x,则x= _________ .
11.(2012?凉山州)整式A与m2﹣2mn+n2的和是(m+n)2,则A= _____ ____ .
12.(2001?天津)已知x+y=4,且x﹣y=10,则2xy= ___ ______ .
13.(2005?威海)若a+b=6,ab=4,则a﹣b= _____ ____ .
14.(2007?天津)已知x+y=7且xy=12,则当x<y时,的值等于 _________ .
15.(2012?江西)已知(m﹣n)2=8,(m+n)2=2,则m2+n2= _____ ____ .
16.(2003?徐州)计算:(3a2b)2+(8a6b2)÷(﹣2a2b)
17.计算:a×(3a2b)3÷(﹣)×
18.计算:3a3b2÷a2+b?(a2b﹣3ab﹣5a2b)
19.计算:[x(x2y2﹣xy)﹣y(x2+x3y)]÷3x2y.
学校:___________________ 姓名:___________________ 成绩:____________________
<二>、选做题
1.(2+1)(22+1)(24+1)的结果为 _________ .
2.(2009?北京)若把代数式x2﹣2x﹣3化为(x﹣m)2+k的形式,其中m,k为常数,则m+k= _________ .
3.计算:= _________ .
4.(2004?天津)已知x2+y2=25,x+y=7,且x>y,则x﹣y的值等于 _________ .
5.已知(2009﹣a)(2008﹣a)=2007,那么(2009﹣a)2+(2008﹣a)2= _________ .
6.(2009?烟台)设a>b>0,a2+b2﹣6ab=0,则的值等于 _________ .
7.若x﹣y=2,x2+y2=4,则x2004+y2004的值是 _________ .
8.(2011?乐山)若m为正实数,且,则= _____ ____ .
9.(2011?天津)若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是( )
A.
x+y+z=0
B.
x+y﹣2z=0
C.
y+z﹣2x=0
D.
z+x﹣2y=0
10.(2010?内江)已知m2﹣5m﹣1=0,则= _________ .
11.(2011?达州)若,则= _________ .
12.(2001?常州)已知x+y=1,则代数式x3+3xy+y3的值是 _________ .
13.计算:4x(x﹣1)2+x(2x+5)(5﹣2x)= _______ __ .
同课章节目录
