山东省聊城市某重点中学2012-2013学年高二上学期第四次模块检测文科数学试题
文档属性
| 名称 | 山东省聊城市某重点中学2012-2013学年高二上学期第四次模块检测文科数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-17 00:00:00 | ||
图片预览



文档简介
山东省聊城市某重点中学2012-2013学年高二上学期第四次模块检测文科数学试题
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、选择题
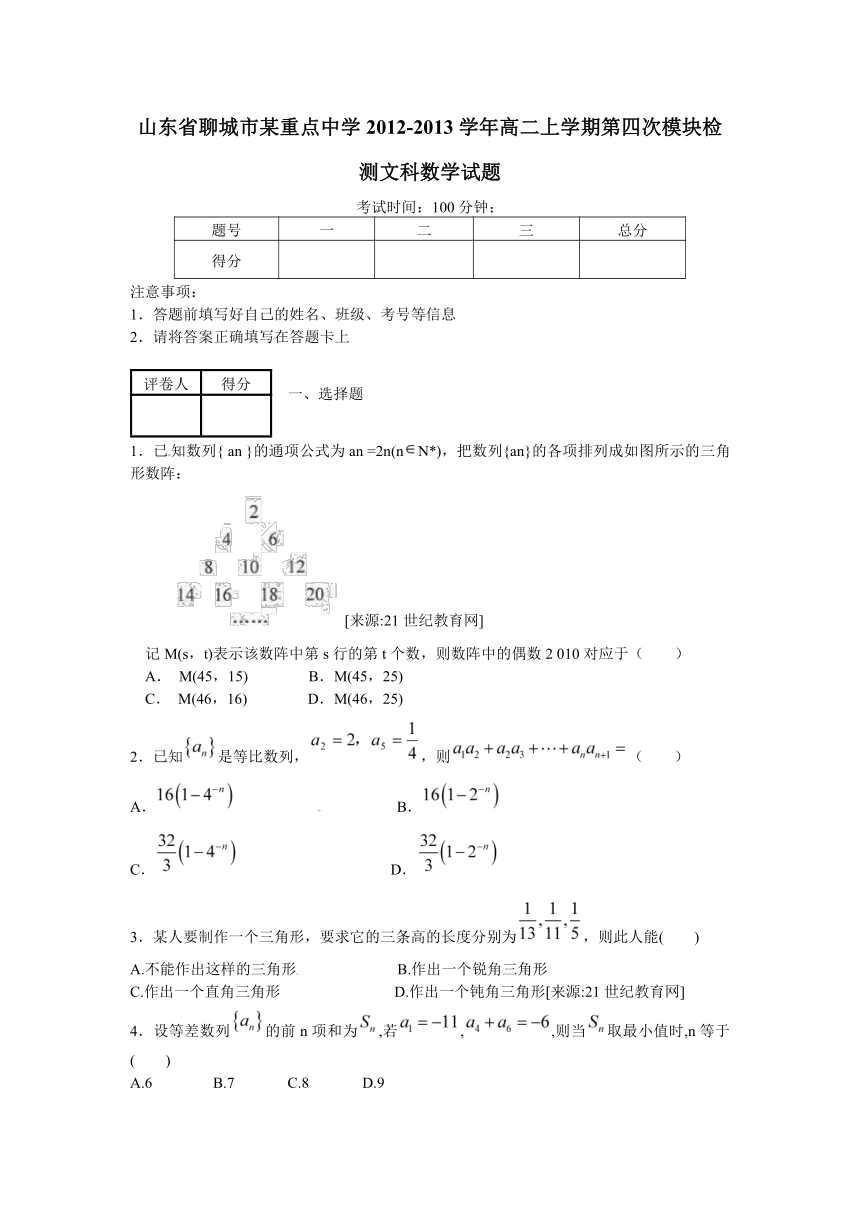
1.已知数列{ an }的通项公式为an =2n(nN*),把数列{an}的各项排列成如图所示的三角形数阵:
[来源:21世纪教育网]
记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2 010对应于( )
A. M(45,15) B.M(45,25)
C. M(46,16) D.M(46,25)
2.已知是等比数列,,则( )
A. B.
C. D.
3.某人要制作一个三角形,要求它的三条高的长度分别为,则此人能( )
A.不能作出这样的三角形 B.作出一个锐角三角形
C.作出一个直角三角形 D.作出一个钝角三角形[来源:21世纪教育网]
4.设等差数列的前n项和为,若,,则当取最小值时,n等于( )
A.6 B.7 C.8 D.9
5.等腰三角形一腰上的高是,这条高与底边的夹角为,则底边长=( )
A.2 B. C.3 D.
6.若实数满足则的最小值是( )
A.0 B.1 C. D.9
7.古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如:
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数。下列数中既是三角形数又是正方形数的是( )
A.289 B.1024 C.1225 D.1378
8.设满足则 ( )
A.有最小值2,最大值3 B.有最小值2,无最大值
C.有最大值3,无最小值 D.既无最小值,也无最大值
9.已知是数列{}的前n项和,,那么数列{}是( )
A.等比数列 B.当p≠0时为等比数列
C.当p≠0,p≠1时为等比数列 D.不可能为等比数列
10.设{an}是由正数组成的等比数列,公比q=2,且a1·a2·a3·…·a30=230,那么a3·a6·a9·…·a30等于( )
A.210 B.220 C.216 D.215
11.已知则的等差中项为( )
A. B. C. D.
12.已知等差数列{ an }的公差为d(d≠0),且a3+ a 6+ a 10+ a 13=32,若am=8,则m为( )
A.12 B. 8 C.6 D.4
第II卷(非选择题)
评卷人
得分
[来源:21世纪教育网]
二、填空题
13.已知等差数列满足,则它的前10项和______
14.已知数列的首项为,且,则这个数列的通项公式为___________
15.若,且当时,恒有,则以,b
为坐标点P(,b)所形成的平面区域的面积等于_______
16.设数列通项公式为,则
评卷人
得分
三、解答题
17.在△ABC中,A最大,C最小,且A=2C,a+c=2b,求此三角形的三边之比.
18.已知数列的各项均为正数,Sn为其前n项和,对于任意,满足关系. 21世纪教育网
(Ⅰ)证明:是等比数列;
(Ⅱ)在正数数列中,设,求数列中的最大项.
19.在数列中,,
(I)求数列的通项公式;
(II)求数列的前项和
20.在三角形中,,求三角形的面积。
21.已知是一个等差数列,且,.
(Ⅰ)求的通项; (Ⅱ)求前n项和Sn的最大值.
[21世纪教育网
21世纪教育网
21世纪教育网
高二文数学参考答案
一、选择题
1.A??????
解析:由数阵的排列规律知,数阵中的前n行共有1+2+3+…+n=,当n=44时,共有990项,又数阵中的偶数2 010是数列{an }的第1 005项,且+15=1 005,因此2010是数阵中第45行的第15个数故选A
2.C??????
解析:等比数列的公比,显然数列也是等比数列,其首项为,公比,。
3.D??????
解析:设三边分别为a,b,c,利用面积相等可知 由余弦定理得,所以角A为钝角
4.A??????
解析:设该数列的公差为,则,解得, 所以,所以当时,取最小值。
5.D??????6.B??????
解析:解出可行域的顶点,带入验证。 21世纪教育网
7.C??????8.B??????9.D??????10.B??????
解析:由等比数列的定义,a1 ·a2 ·a3 =()3 ,故a1 ·a2 ·a3 ·…·a30 =()3 .又q=2,故a3 ·a6 ·a9 ·…·a30 =220 .
11.A??????12.B??????
解析:由等差中项的性质可得+++=32=4,故=8,则m=8
二、填空题
13.95
14.
15.1
16.153
三、解答题
17.解:由正弦定理得 ===2cosC,即cosC=. ??? 由余弦定理得cosC==, ∵a+c=2b, ∴cosC==, ∴=. ??? 整理得,
18.(Ⅰ)证明:∵? ① ∴? ②? ②-①,得 ∵ 故数列是等比数列21世纪教育网21世纪教育网
19.解:(I)由已知有 ? 利用累差迭加即可求出数列的通项公式: () (II)由(I)知, = 而,又是一个典型的错位相减法模型, 易得 =
20.由题意,得为锐角,, ??? , ??? 由正弦定理得 ,? .
21.(Ⅰ)设的公差为,由已知条件,,解出,. 所以. (Ⅱ).所以时,取到最大值.
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、选择题
1.已知数列{ an }的通项公式为an =2n(nN*),把数列{an}的各项排列成如图所示的三角形数阵:
[来源:21世纪教育网]
记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2 010对应于( )
A. M(45,15) B.M(45,25)
C. M(46,16) D.M(46,25)
2.已知是等比数列,,则( )
A. B.
C. D.
3.某人要制作一个三角形,要求它的三条高的长度分别为,则此人能( )
A.不能作出这样的三角形 B.作出一个锐角三角形
C.作出一个直角三角形 D.作出一个钝角三角形[来源:21世纪教育网]
4.设等差数列的前n项和为,若,,则当取最小值时,n等于( )
A.6 B.7 C.8 D.9
5.等腰三角形一腰上的高是,这条高与底边的夹角为,则底边长=( )
A.2 B. C.3 D.
6.若实数满足则的最小值是( )
A.0 B.1 C. D.9
7.古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如:
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数。下列数中既是三角形数又是正方形数的是( )
A.289 B.1024 C.1225 D.1378
8.设满足则 ( )
A.有最小值2,最大值3 B.有最小值2,无最大值
C.有最大值3,无最小值 D.既无最小值,也无最大值
9.已知是数列{}的前n项和,,那么数列{}是( )
A.等比数列 B.当p≠0时为等比数列
C.当p≠0,p≠1时为等比数列 D.不可能为等比数列
10.设{an}是由正数组成的等比数列,公比q=2,且a1·a2·a3·…·a30=230,那么a3·a6·a9·…·a30等于( )
A.210 B.220 C.216 D.215
11.已知则的等差中项为( )
A. B. C. D.
12.已知等差数列{ an }的公差为d(d≠0),且a3+ a 6+ a 10+ a 13=32,若am=8,则m为( )
A.12 B. 8 C.6 D.4
第II卷(非选择题)
评卷人
得分
[来源:21世纪教育网]
二、填空题
13.已知等差数列满足,则它的前10项和______
14.已知数列的首项为,且,则这个数列的通项公式为___________
15.若,且当时,恒有,则以,b
为坐标点P(,b)所形成的平面区域的面积等于_______
16.设数列通项公式为,则
评卷人
得分
三、解答题
17.在△ABC中,A最大,C最小,且A=2C,a+c=2b,求此三角形的三边之比.
18.已知数列的各项均为正数,Sn为其前n项和,对于任意,满足关系. 21世纪教育网
(Ⅰ)证明:是等比数列;
(Ⅱ)在正数数列中,设,求数列中的最大项.
19.在数列中,,
(I)求数列的通项公式;
(II)求数列的前项和
20.在三角形中,,求三角形的面积。
21.已知是一个等差数列,且,.
(Ⅰ)求的通项; (Ⅱ)求前n项和Sn的最大值.
[21世纪教育网
21世纪教育网
21世纪教育网
高二文数学参考答案
一、选择题
1.A??????
解析:由数阵的排列规律知,数阵中的前n行共有1+2+3+…+n=,当n=44时,共有990项,又数阵中的偶数2 010是数列{an }的第1 005项,且+15=1 005,因此2010是数阵中第45行的第15个数故选A
2.C??????
解析:等比数列的公比,显然数列也是等比数列,其首项为,公比,。
3.D??????
解析:设三边分别为a,b,c,利用面积相等可知 由余弦定理得,所以角A为钝角
4.A??????
解析:设该数列的公差为,则,解得, 所以,所以当时,取最小值。
5.D??????6.B??????
解析:解出可行域的顶点,带入验证。 21世纪教育网
7.C??????8.B??????9.D??????10.B??????
解析:由等比数列的定义,a1 ·a2 ·a3 =()3 ,故a1 ·a2 ·a3 ·…·a30 =()3 .又q=2,故a3 ·a6 ·a9 ·…·a30 =220 .
11.A??????12.B??????
解析:由等差中项的性质可得+++=32=4,故=8,则m=8
二、填空题
13.95
14.
15.1
16.153
三、解答题
17.解:由正弦定理得 ===2cosC,即cosC=. ??? 由余弦定理得cosC==, ∵a+c=2b, ∴cosC==, ∴=. ??? 整理得,
18.(Ⅰ)证明:∵? ① ∴? ②? ②-①,得 ∵ 故数列是等比数列21世纪教育网21世纪教育网
19.解:(I)由已知有 ? 利用累差迭加即可求出数列的通项公式: () (II)由(I)知, = 而,又是一个典型的错位相减法模型, 易得 =
20.由题意,得为锐角,, ??? , ??? 由正弦定理得 ,? .
21.(Ⅰ)设的公差为,由已知条件,,解出,. 所以. (Ⅱ).所以时,取到最大值.
同课章节目录
